20. 某公园有一块长方形绿地$ABCD$,$BC$为$\sqrt{162}m$,$AB$为$\sqrt{128}m$,内有一块长方形花坛(即图中阴影部分),长为$(\sqrt{13}+1)m$,宽为$(\sqrt{13}-1)m$。
(1)求长方形$ABCD$的周长;(5分)
(2)图中的空白部分另作他用,需要$50$元/平方米的定期维护费,求定期维护的总费用。(5分)
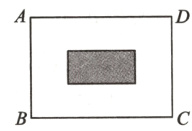
(1)求长方形$ABCD$的周长;(5分)
(2)图中的空白部分另作他用,需要$50$元/平方米的定期维护费,求定期维护的总费用。(5分)

答案:
解:$\sqrt{162}=9\sqrt{2}$,$\sqrt{128}=8\sqrt{2}$。
(1)长方形$ABCD$的周长为:$2(9\sqrt{2}+8\sqrt{2})=2\times17\sqrt{2}=34\sqrt{2}(m)$,答:长方形$ABCD$的周长是$34\sqrt{2}m$。
(2)定期维护的总费用为:$50\times[9\sqrt{2}\times8\sqrt{2}-(\sqrt{13}+1)(\sqrt{13}-1)]=50\times(144 - 12)=6600$(元)。答:定期维护的总费用为$6600$元。
(1)长方形$ABCD$的周长为:$2(9\sqrt{2}+8\sqrt{2})=2\times17\sqrt{2}=34\sqrt{2}(m)$,答:长方形$ABCD$的周长是$34\sqrt{2}m$。
(2)定期维护的总费用为:$50\times[9\sqrt{2}\times8\sqrt{2}-(\sqrt{13}+1)(\sqrt{13}-1)]=50\times(144 - 12)=6600$(元)。答:定期维护的总费用为$6600$元。
21. 大家知道$\sqrt{2}$是无理数,而无理数是无限不循环小数,因此$\sqrt{2}$的小数部分我们不可能全部写出来,而$1<\sqrt{2}<2$,于是可用$\sqrt{2}-1$来表示$\sqrt{2}$的小数部分。请解答下列问题:
(1)$\sqrt{21}$的整数部分是______,小数部分是__________。(6分)
(2)如果$\sqrt{7}$的小数部分为$a$,$\sqrt{15}-1$的整数部分为$b$,求$a + b-\sqrt{7}$的值。(6分)
(1)$\sqrt{21}$的整数部分是______,小数部分是__________。(6分)
(2)如果$\sqrt{7}$的小数部分为$a$,$\sqrt{15}-1$的整数部分为$b$,求$a + b-\sqrt{7}$的值。(6分)
答案:
(1)$4$ $\sqrt{21}-4$
(2)解:$\because\sqrt{4}<\sqrt{7}<\sqrt{9}$,$\therefore 2<\sqrt{7}<3$,$\because\sqrt{7}$的小数部分为$a$,$\therefore a=\sqrt{7}-2$,$\because\sqrt{9}<\sqrt{15}<\sqrt{16}$,$\therefore 3<\sqrt{15}<4$,$\therefore 2<\sqrt{15}-1<3$,$\because\sqrt{15}-1$的整数部分为$b$,$\therefore b = 2$,$\therefore a + b-\sqrt{7}=\sqrt{7}-2 + 2-\sqrt{7}=0$。
(1)$4$ $\sqrt{21}-4$
(2)解:$\because\sqrt{4}<\sqrt{7}<\sqrt{9}$,$\therefore 2<\sqrt{7}<3$,$\because\sqrt{7}$的小数部分为$a$,$\therefore a=\sqrt{7}-2$,$\because\sqrt{9}<\sqrt{15}<\sqrt{16}$,$\therefore 3<\sqrt{15}<4$,$\therefore 2<\sqrt{15}-1<3$,$\because\sqrt{15}-1$的整数部分为$b$,$\therefore b = 2$,$\therefore a + b-\sqrt{7}=\sqrt{7}-2 + 2-\sqrt{7}=0$。
查看更多完整答案,请扫码查看


