《2025年课堂点睛八年级数学下册人教版安徽专版》

六(本题满分12分)
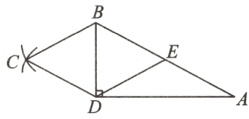
21. 如图,在△ABD中,∠ADB = 90°,∠A = 30°,AB = 10,E是边AB的中点.分别以点B,D为圆心,BE的长为半径作弧,两弧交于点C,连接CB,CD.
(1)根据以上尺规作图的过程,四边形BCDE是什么特殊四边形？说明理由.(6分)
(2)求四边形BCDE的面积.(6分)

答案：

(1)解：四边形BCDE是菱形。理由如下：$\because\angle ADB = 90^{\circ},E$是边AB的中点，$\therefore DE = BE=\frac{1}{2}AB$。由作图知$BC = CD = BE,\therefore BC = CD = DE = BE.\therefore$四边形BCDE是菱形。
(2)如图C ，连接CE交BD于点F。$\because\angle ADB = 90^{\circ},\angle A = 30^{\circ},AB = 10,\therefore BD=\frac{1}{2}AB = 5$。由
(1)知$BE=\frac{1}{2}AB = 5$。又四边形BCDE是菱形，$\therefore BD\perp CE,BF=\frac{1}{2}BD=\frac{5}{2},CE = 2EF$。在$Rt\triangle BEF$中，$EF=\sqrt{BE^{2}-BF^{2}}=\sqrt{5^{2}-(\frac{5}{2})^{2}}=\frac{5\sqrt{3}}{2}.\therefore CE = 5\sqrt{3}.\therefore S_{菱形BCDE}=\frac{1}{2}CE\cdot BD=\frac{1}{2}\times5\sqrt{3}\times5=\frac{25\sqrt{3}}{2}$。

七(本大题满分12分)
22. 如图①所示的赵爽弦图由四个全等的直角三角形拼成,利用它可以证明勾股定理.思路是大正方形的面积有两种求法,这里用两种求法来表示同一个量从而得到等式的方法,我们称之为“双求法”.请你用“双求法”解决下面问题：
(1)请你利用图①的赵爽弦图,推导勾股定理;(4分)
(2)如图②,在Rt△ABC中,∠ACB = 90°,CD是AB边上的高,AC = 3,BC = 4,求CD的长度;(4分)
(3)如图③,在△ABC中,AD是BC边上的高,AB = 4,AC = 5,BC = 6,设BD = x,求AD的长度.(4分)

答案：
(1)证明：$\because$大正方形的面积有两种求法：一种是$c^{2}$，另一种为$(b - a)^{2}+4\times\frac{1}{2}ab;\therefore c^{2}=(b - a)^{2}+4\times\frac{1}{2}ab=a^{2}+b^{2}+2ab - 2ab=a^{2}+b^{2}$；
(2)解：在$Rt\triangle ABC$中，$AB=\sqrt{3^{2}+4^{2}}=5$，由面积的两种算法可得：$S_{\triangle ABC}=\frac{1}{2}\times3\times4=\frac{1}{2}\times5\times CD$，解得$CD=\frac{12}{5}$；
(3)解：在$Rt\triangle ABD$中，$AD^{2}=4^{2}-x^{2}=16 - x^{2}$，在$Rt\triangle ADC$中，$AD^{2}=5^{2}-(6 - x)^{2}=-11 + 12x - x^{2}$，所以$16 - x^{2}=-11 + 12x - x^{2}$，解得$x=\frac{9}{4},\therefore AD=\sqrt{AB^{2}-BD^{2}}=\sqrt{4^{2}-(\frac{9}{4})^{2}}=\frac{5\sqrt{7}}{4}$。