《2025年课堂点睛八年级数学下册人教版安徽专版》

17. 如图，四边形ABCD是平行四边形，DE//BF，且分别交对角线AC于点E，F，连接BE，DF.
（1）求证：AE = CF；（4分）
（2）若BE = DE，求证：四边形EBFD为菱形.（4分）

答案： 证明：
(1)
∵四边形ABCD是平行四边形，
∴AD = CB，AD//CB，
∴∠DAE = ∠BCF.
∵DE//BF，
∴∠DEF = ∠BFE，
∴∠AED = ∠CFB. 在△ADE和△CBF中，{∠DAE = ∠BCF，∠AED = ∠CFB，AD = CB}，
∴△ADE≌△CBF(AAS).
∴AE = CF.
(2)由
(1)知△ADE≌△CBF，则DE = BF. 又
∵DE//BF，
∴四边形EBFD是平行四边形.
∵BE = DE，
∴四边形EBFD为菱形.

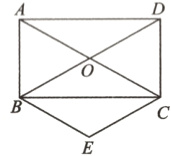
18. 已知：如图，平行四边形ABCD的对角线AC、BD相交于点O，BE//AC，CE//DB，且∠BOC + 2∠OBC = 180°.
（1）求证：四边形ABCD是矩形；（4分）
（2）若∠AOB = 60°，AB = 2，求四边形OBEC的面积.（4分）

答案：
(1)证明：
∵∠BOC + 2∠OBC = 180°，∠BOC + ∠OBC + ∠ACB = 180°，
∴∠OBC = ∠OCB，
∴OB = OC.
∵四边形ABCD是平行四边形，
∴OA = OC，OB = OD，
∴AC = BD，
∴四边形ABCD是矩形.
(2)解：由
(1)可知，OA = OB = OC，四边形ABCD是矩形，
∴∠ABC = 90°.
∵∠AOB = 60°，
∴△OAB是等边三角形，OA = AB = 2，
∴AC = 2OA = 4，
∴BC = √(AC² - AB²)=√(4² - 2²)=2√3.
∵BE//AC，CE//DB，
∴四边形OBEC是平行四边形，
∴S平行四边形OBEC = 2S△OBC = S△ABC = 1/2BC·AB = 1/2×2√3×2 = 2√3.

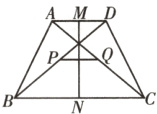
19. 如图，在四边形ABCD中，AB = CD，M，N，P，Q分别是AD，BC，BD，AC的中点. 求证：MN与PQ互相垂直平分.

答案： 证明：连接MP，NQ，PN，MQ，
∵M，N，P，Q分别是AD，BC，BD，AC的中点，
∴PM//1/2AB，NQ//1/2AB，
∴PM//NQ，
∴四边形MPNQ为平行四边形. 同理PN//1/2CD，而CD = AB，
∴PN = PM，
∴四边形MPNQ为菱形，
∴MN与PQ互相垂直平分.