搜索
18. 如图，有一张四边形纸片ABCD，AB⊥BC. 经测得AB = 9cm，BC = 12cm，CD = 8cm，AD = 17cm.
（1）求A、C两点之间的距离；（4分）
（2）求这张纸片的面积.（4分）
（1）求A、C两点之间的距离；（4分）
（2）求这张纸片的面积.（4分）
答案：
(1) 解：连接$AC$，如图.
在$Rt\triangle ABC$中，$AB\perp BC$，$AB = 9cm$，$BC = 12cm$，$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{9^{2}+12^{2}} = 15cm$. 即$A$、$C$两点之间的距离为$15cm$；
(2) $\because CD^{2}+AC^{2}=8^{2}+15^{2}=17^{2}=AD^{2}$，$\therefore \angle ACD = 90^{\circ}$，$\therefore$四边形纸片$ABCD$的面积为$S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD=\frac{1}{2}\times9\times12+\frac{1}{2}\times15\times8 = 54 + 60 = 114(cm^{2})$.
(1) 解：连接$AC$，如图.
在$Rt\triangle ABC$中，$AB\perp BC$，$AB = 9cm$，$BC = 12cm$，$\therefore AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{9^{2}+12^{2}} = 15cm$. 即$A$、$C$两点之间的距离为$15cm$；(2) $\because CD^{2}+AC^{2}=8^{2}+15^{2}=17^{2}=AD^{2}$，$\therefore \angle ACD = 90^{\circ}$，$\therefore$四边形纸片$ABCD$的面积为$S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD=\frac{1}{2}\times9\times12+\frac{1}{2}\times15\times8 = 54 + 60 = 114(cm^{2})$.
19. 为了加强青少年防溺水安全教育，5月底某校开展了“远离溺水，珍爱生命”的防溺水安全知识比赛. 下面是从参赛学生中随机收集到的20名学生的成绩（单位:分）:
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
分析数据:
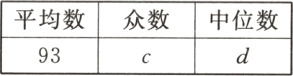
解决问题:
（1）直接写出上面表格中的a，b，c，d的值；（4分）
（2）若成绩达到95分及以上为“优秀”等级，求“优秀”等级所占的百分率；（3分）
（3）请估计该校1500名学生中成绩达到95分及以上的学生人数.（3分）
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
分析数据:
解决问题:
（1）直接写出上面表格中的a，b，c，d的值；（4分）
（2）若成绩达到95分及以上为“优秀”等级，求“优秀”等级所占的百分率；（3分）
（3）请估计该校1500名学生中成绩达到95分及以上的学生人数.（3分）
答案：
(1) 解：$\because 91$分的有$4$人，$97$分的有$3$人，$\therefore a = 4$，$b = 3$，$\because 91$分的人数最多，$\therefore$众数为$91$，即$c = 91$，$d=\frac{91 + 95}{2}=93$，综上所述，$a = 4$，$b = 3$，$c = 91$，$d = 93$.
(2) 成绩达到$95$分及以上的有$10$人，则“优秀”等级所占的百分率为：$\frac{10}{20}\times100\% = 50\%$.
(3) 估计该校$1500$名学生中成绩达到$95$分及以上的学生人数为：$1500\times50\% = 750$(人).
(1) 解：$\because 91$分的有$4$人，$97$分的有$3$人，$\therefore a = 4$，$b = 3$，$\because 91$分的人数最多，$\therefore$众数为$91$，即$c = 91$，$d=\frac{91 + 95}{2}=93$，综上所述，$a = 4$，$b = 3$，$c = 91$，$d = 93$.
(2) 成绩达到$95$分及以上的有$10$人，则“优秀”等级所占的百分率为：$\frac{10}{20}\times100\% = 50\%$.
(3) 估计该校$1500$名学生中成绩达到$95$分及以上的学生人数为：$1500\times50\% = 750$(人).
20. 如图，以等腰直角三角形AOB的斜边为直角边向外作第2个等腰直角三角形ABA1，再以等腰直角三角形ABA1的斜边为直角边向外作第3个等腰直角三角形A1BB1 ……如此作下去，若OA = OB = 1.
（1）A1B = _____，$S_{\triangle A_{1}B_{1}A_{2}}$ = _____；（4分）
（2）试猜想第n个等腰直角三角形的面积Sn.（6分）
（1）A1B = _____，$S_{\triangle A_{1}B_{1}A_{2}}$ = _____；（4分）
（2）试猜想第n个等腰直角三角形的面积Sn.（6分）
答案：
(1) 2 4
(2) 解：$\because OA = OB = 1$，$\angle AOB = 90^{\circ}$，$\therefore AB=\sqrt{2}$，$S_{1}=\frac{1}{2}\times1\times1=\frac{1}{2}=2^{-1}$.$\therefore AA_{1}=AB=\sqrt{2}$，$\angle A_{1}AB = 90^{\circ}$，$\therefore A_{1}B = 2$，$S_{2}=\frac{1}{2}\times\sqrt{2}\times\sqrt{2}=1 = 2^{0}$.$\because BB_{1}=A_{1}B = 2$，$\angle A_{1}BB_{1}=90^{\circ}$，$\therefore A_{1}B_{1}=2\sqrt{2}$，$S_{3}=\frac{1}{2}\times2\times2 = 2 = 2^{1}$.$\because A_{1}A_{2}=A_{1}B_{1}=2\sqrt{2}$，$\angle A_{2}A_{1}B_{1}=90^{\circ}$，$\therefore A_{2}B_{1}=4$，$S_{4}=\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}=4 = 2^{2}$. 由此可猜想$S_{n}=2^{n - 2}$.
(1) 2 4
(2) 解：$\because OA = OB = 1$，$\angle AOB = 90^{\circ}$，$\therefore AB=\sqrt{2}$，$S_{1}=\frac{1}{2}\times1\times1=\frac{1}{2}=2^{-1}$.$\therefore AA_{1}=AB=\sqrt{2}$，$\angle A_{1}AB = 90^{\circ}$，$\therefore A_{1}B = 2$，$S_{2}=\frac{1}{2}\times\sqrt{2}\times\sqrt{2}=1 = 2^{0}$.$\because BB_{1}=A_{1}B = 2$，$\angle A_{1}BB_{1}=90^{\circ}$，$\therefore A_{1}B_{1}=2\sqrt{2}$，$S_{3}=\frac{1}{2}\times2\times2 = 2 = 2^{1}$.$\because A_{1}A_{2}=A_{1}B_{1}=2\sqrt{2}$，$\angle A_{2}A_{1}B_{1}=90^{\circ}$，$\therefore A_{2}B_{1}=4$，$S_{4}=\frac{1}{2}\times2\sqrt{2}\times2\sqrt{2}=4 = 2^{2}$. 由此可猜想$S_{n}=2^{n - 2}$.
查看更多完整答案，请扫码查看
