《2025年课堂点睛八年级数学下册人教版安徽专版》

13. 如图，在矩形ABCD中，AB = 3，对角线AC，BD交于点O，DH⊥AC，垂足为H. 若∠ADH = 2∠CDH，则AD的长为______。

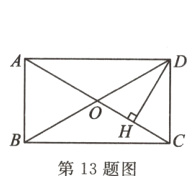
答案： 3√3

14. 如图，在正方形ABCD中，AB = 3$\sqrt{2}$，E为对角线AC上的一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE，EF为邻边作矩形DEFG，连接CG.
（1）若DG = 4，则矩形DEFG的面积为______。
（2）CE + CG的值是______。

答案：
(1)16　
(2)6

15. 如图，在□ABCD中，E，F分别是AB，CD延长线上的点，且BE = DF，连接EF分别交AD，BC于点G，H. 求证：FG = EH.

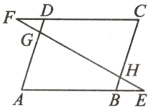
答案： 证明：
∵四边形ABCD是平行四边形，
∴AB//CD，∠A = ∠C，
∴∠E = ∠F，∠A = ∠FDG，∠EBH = ∠C，
∴∠EBH = ∠FDG.
在△EBH与△FDG中，{∠E = ∠F，BE = DF，∠EBH = ∠FDG}，
∴△EBH≌△FDG(ASA)，
∴FG = EH.

16. 如图，在四边形ABCD中，AB//CD，E，F为对角线AC上两点，且AE = CF，DF//BE. 求证：四边形ABCD为平行四边形.

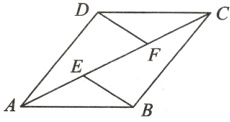
答案： 证明：
∵AB//CD，
∴∠DCA = ∠BAC.
∵DF//BE，
∴∠DFA = ∠BEC，
∴∠AEB = ∠CFD. 在△AEB和△CFD中，{∠AEB = ∠CFD，AE = CF，∠EAB = ∠FCD}，
∴△AEB≌△CFD(ASA).
∴AB = CD.
∵AB//CD，
∴四边形ABCD为平行四边形.