《2025年课堂点睛八年级数学下册人教版安徽专版》

20. 如图，已知菱形ABCD，点E、F是对角线BD所在直线上的两点，且∠AED = 45°，DF = BE，连接CE、AF、CF、AE，得四边形AECF.
（1）求证：四边形AECF是正方形；（5分）
（2）若BD = 4，BE = 3，求菱形ABCD的面积.（5分）

答案：
(1)证明：连接AC，交BD于点O，
∵四边形ABCD是菱形，
∴AO = CO，BO = DO，AC⊥BD.
∵BE = DF，
∴BE + OB = DF + DO，
∴FO = EO，
∴EF与AC垂直且互相平分，
∴四边形AECF是菱形，
∴∠AEF = ∠CEF. 又
∵∠AED = 45°，
∴∠AEC = 90°，
∴四边形AECF是正方形.
(2)解：
∵BD = 4，BE = 3，
∴FD = 3，
∴EF = 10，
∴AC = 10，
∴菱形ABCD的面积 = 1/2AC·BD = 1/2×10×4 = 20.

六（本题满分12分）
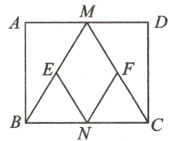
21. 如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点.
（1）求证：△ABM≌△DCM；（6分）
（2）当AB∶AD的值为多少时，四边形MENF是正方形？请说明理由.（6分）

答案：
(1)证明：
∵四边形ABCD是矩形，
∴AB = DC，∠A = ∠D = 90°.
∵M为AD的中点，
∴AM = DM. 在△ABM和△DCM中，{AM = DM，∠A = ∠D，AB = DC}，
∴△ABM≌△DCM(SAS).
(2)解：当AB:AD = 1:2时，四边形MENF是正方形. 理由：当AB:AD = 1:2时，AB = 1/2AD = AM，
∴∠AMB = 45°. 同理∠DMC = 45°，
∴∠EMF = 90°.
∵△ABM≌△DCM，
∴BM = CM.
∵点N，E，F分别是线段BC，BM，CM的中点，
∴FN//BM，EN//CM；FN = 1/2BM，EN = 1/2CM.
∴四边形MENF是平行四边形，FN = EN，
∴四边形MENF是菱形.
∵∠EMF = 90°，
∴四边形MENF是正方形.