20. 阅读材料:一般地,设平面上任意两点A$(x_1,y_1)$和B$(x_2,y_2)$可以用|AB|表示A,B两点之间的距离,那么该如何计算|AB|呢?作AA′⊥x轴、BB′⊥x轴,垂足分别是点A′,B′;作AA″⊥y轴,垂足为点A″,作BB″⊥y轴,垂足为点B″,且与AA′交于点C,则四边形BB′A′C、四边形ACB″A″是矩形。
∵|BC| = |$x_2 - x_1$|,|AC| = |$y_2 - y_1$|,
∴|AB|² = |BC|² + |AC|² = $(x_2 - x_1)^{2} + (y_2 - y_1)^{2}$。
∴|AB| = $\sqrt{(x_2 - x_1)^{2} + (y_2 - y_1)^{2}}$。
这就是平面直角坐标系中两点之间的距离公式。
如:点A(1,4)和点B(5,2)之间的距离|AB| = $\sqrt{(5 - 1)^{2} + (2 - 4)^{2}}$ = $\sqrt{20}$ = $2\sqrt{5}$。
(1)请运用公式计算点M(4,2)和点N(2, - 1)之间的距离;(4分)
(2)在(1)的条件下,点O为原点;求△MNO的周长。(6分)
∵|BC| = |$x_2 - x_1$|,|AC| = |$y_2 - y_1$|,
∴|AB|² = |BC|² + |AC|² = $(x_2 - x_1)^{2} + (y_2 - y_1)^{2}$。
∴|AB| = $\sqrt{(x_2 - x_1)^{2} + (y_2 - y_1)^{2}}$。
这就是平面直角坐标系中两点之间的距离公式。
如:点A(1,4)和点B(5,2)之间的距离|AB| = $\sqrt{(5 - 1)^{2} + (2 - 4)^{2}}$ = $\sqrt{20}$ = $2\sqrt{5}$。
(1)请运用公式计算点M(4,2)和点N(2, - 1)之间的距离;(4分)
(2)在(1)的条件下,点O为原点;求△MNO的周长。(6分)
答案:
(1)解:|MN| = $\sqrt{(4 - 2)² + (2 + 1)²}$ = $\sqrt{13}$,
∴点 M(4,2)和点 N(2,-1)之间的距离是$\sqrt{13}$.
(2)
∵|MO| = $\sqrt{(4 - 0)² + (2 - 0)²}$ = 2$\sqrt{5}$,|NO| = $\sqrt{(2 - 0)² + (-1 - 0)²}$ = $\sqrt{5}$,
∴△MNO 的周长 = |MN| + |MO| + |NO| = $\sqrt{13}$ + 3$\sqrt{5}$.
(1)解:|MN| = $\sqrt{(4 - 2)² + (2 + 1)²}$ = $\sqrt{13}$,
∴点 M(4,2)和点 N(2,-1)之间的距离是$\sqrt{13}$.
(2)
∵|MO| = $\sqrt{(4 - 0)² + (2 - 0)²}$ = 2$\sqrt{5}$,|NO| = $\sqrt{(2 - 0)² + (-1 - 0)²}$ = $\sqrt{5}$,
∴△MNO 的周长 = |MN| + |MO| + |NO| = $\sqrt{13}$ + 3$\sqrt{5}$.
六(本题满分12分)
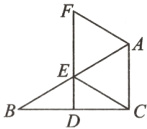
21. 如图,在△ABC中,∠ACB = 90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF = 2DE,连接CE,AF。
(1)求证:AF = CE;(6分)
(2)当∠B = 30°时,试判断四边形ACEF的形状,并说明理由。(6分)
21. 如图,在△ABC中,∠ACB = 90°,点D,E分别是边BC,AB的中点,连接DE并延长至点F,使EF = 2DE,连接CE,AF。
(1)求证:AF = CE;(6分)
(2)当∠B = 30°时,试判断四边形ACEF的形状,并说明理由。(6分)

答案:
(1)证明:
∵点 D,E 分别是边 BC,AB 的中点,
∴DE 是△ABC 的中位线.
∴DE//AC,AC = 2DE.
∵EF = 2DE,
∴EF = AC.又
∵EF//AC,
∴四边形 ACEF 是平行四边形.
∴AF = CE.
(2)解:当∠B = 30°时,四边形 ACEF 是菱形.理由如下:
∵∠ACB = 90°,∠B = 30°,点 E 为 AB 的中点,
∴CE = $\frac{1}{2}$AB,AC = $\frac{1}{2}$AB.
∴AC = CE.由
(1)可知四边形 ACEF 是平行四边形,
∴四边形 ACEF 是菱形.
(1)证明:
∵点 D,E 分别是边 BC,AB 的中点,
∴DE 是△ABC 的中位线.
∴DE//AC,AC = 2DE.
∵EF = 2DE,
∴EF = AC.又
∵EF//AC,
∴四边形 ACEF 是平行四边形.
∴AF = CE.
(2)解:当∠B = 30°时,四边形 ACEF 是菱形.理由如下:
∵∠ACB = 90°,∠B = 30°,点 E 为 AB 的中点,
∴CE = $\frac{1}{2}$AB,AC = $\frac{1}{2}$AB.
∴AC = CE.由
(1)可知四边形 ACEF 是平行四边形,
∴四边形 ACEF 是菱形.
七(本题满分12分)
22. 李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:
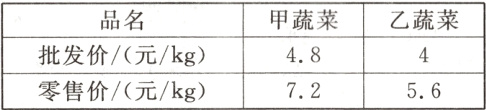
(1)若他批发甲、乙两种蔬菜共40kg花费180元,求批发甲、乙两种蔬菜各多少千克?(列方程或方程组求解)(4分)
(2)若他批发甲、乙两种蔬菜共80kg花费m元,设批发甲种蔬菜nkg,求m与n的函数关系式;(4分)
(3)在(2)的条件下,全部卖完蔬菜后要保证利润不低于176元,至少批发甲种蔬菜多少千克?(4分)
22. 李叔叔批发甲、乙两种蔬菜到菜市场去卖,已知甲、乙两种蔬菜的批发价和零售价如下表所示:

(1)若他批发甲、乙两种蔬菜共40kg花费180元,求批发甲、乙两种蔬菜各多少千克?(列方程或方程组求解)(4分)
(2)若他批发甲、乙两种蔬菜共80kg花费m元,设批发甲种蔬菜nkg,求m与n的函数关系式;(4分)
(3)在(2)的条件下,全部卖完蔬菜后要保证利润不低于176元,至少批发甲种蔬菜多少千克?(4分)
答案:
(1)解:设批发甲种蔬菜 x 千克,批发乙种蔬菜 y 千克,根据题意得$\begin{cases}x + y = 40\\4.8x + 4y = 180\end{cases}$,解得$\begin{cases}x = 25\\y = 15\end{cases}$.答:批发甲种蔬菜 25 千克,批发乙种蔬菜 15 千克.
(2)根据题意得 m = 4.8n + (80 - n)×4,整理得 m = 0.8n + 320.
(3)设全部卖完蔬菜后利润为 w 元,根据题意得 w = (7.2 - 4.8)n + (5.6 - 4)(80 - n),整理得 w = 0.8n + 128,
∵要保证利润不低于 176 元,
∴w = 0.8n + 128≥176,解得 n≥60,
∴至少批发甲种蔬菜 60 千克.
(1)解:设批发甲种蔬菜 x 千克,批发乙种蔬菜 y 千克,根据题意得$\begin{cases}x + y = 40\\4.8x + 4y = 180\end{cases}$,解得$\begin{cases}x = 25\\y = 15\end{cases}$.答:批发甲种蔬菜 25 千克,批发乙种蔬菜 15 千克.
(2)根据题意得 m = 4.8n + (80 - n)×4,整理得 m = 0.8n + 320.
(3)设全部卖完蔬菜后利润为 w 元,根据题意得 w = (7.2 - 4.8)n + (5.6 - 4)(80 - n),整理得 w = 0.8n + 128,
∵要保证利润不低于 176 元,
∴w = 0.8n + 128≥176,解得 n≥60,
∴至少批发甲种蔬菜 60 千克.
查看更多完整答案,请扫码查看


