《2025年课堂点睛八年级数学下册人教版安徽专版》

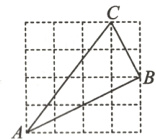
18. 如图,在4×4的方格中,每个小方格的边长为1.
(1)求△ABC的周长;(3分)
(2)求证:∠ABC=90°;(3分)
(3)若P为直线AC上任意一点,则线段BP的最小值为_____.(2分)

答案：
(1)解：$AB=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$，$AC=\sqrt{3^{2}+4^{2}}=5$，$BC=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$\therefore \triangle ABC$的周长为$2\sqrt{5}+5+\sqrt{5}=3\sqrt{5}+5$；
(2)证明：$\because AB^{2}+BC^{2}=20 + 5 = 25 = AC^{2}$，$\therefore \triangle ABC$是直角三角形，且$\angle ABC = 90^{\circ}$。
(3)2

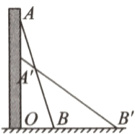
19. 一架梯子AB长25米,如图所示,斜靠在一墙面上.
(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高? (5分)
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米? (5分)
　

答案：
(1)解：在$Rt\triangle AOB$中，$\because AB = 25$米，$OB = 7$米，$\therefore OA=\sqrt{AB^{2}-OB^{2}}=\sqrt{25^{2}-7^{2}}=24$(米)。答：梯子的顶端距地面 24 米。
(2)在$Rt\triangle A'O'B'$中，$\because A'O'=24 - 4 = 20$(米)，$\therefore OB'=\sqrt{A'B'^{2}-OA'^{2}}=\sqrt{25^{2}-20^{2}}=15$(米)，$BB'=15 - 7 = 8$(米)。答：梯子的底端在水平方向滑动了 8 米。

20. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.

答案： 解：$\because \angle B = 90^{\circ}$，$\therefore \triangle ABC$为直角三角形，又$\because AB = 3$，$BC = 4$，$\therefore$根据勾股定理得：$AC=\sqrt{AB^{2}+BC^{2}}=5$，又$\because CD = 12$，$AD = 13$，$\therefore AD^{2}=13^{2}=169$，$CD^{2}+AC^{2}=12^{2}+5^{2}=144 + 25 = 169$，$\therefore CD^{2}+AC^{2}=AD^{2}$，$\therefore \triangle ACD$为直角三角形，$\angle ACD = 90^{\circ}$，则$S_{四边形ABCD}=S_{\triangle ABC}+S_{\triangle ACD}=\frac{1}{2}AB\cdot BC+\frac{1}{2}AC\cdot CD=\frac{1}{2}\times3\times4+\frac{1}{2}\times5\times12 = 36$。故四边形 ABCD 的面积是 36。