《2025年课堂点睛八年级数学下册人教版安徽专版》

八(本题满分14分)
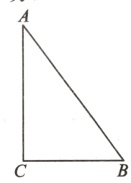
23. 如图,△ABC中,∠C=90°,AB=10cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒1cm,设出发的时间为t秒.
(1)出发2秒后,求△ABP的周长;(4分)
(2)当t为几秒时,BP平分∠ABC;(4分)
(3)问t为何值时,△BCP为等腰三角形? (6分)
　

答案：

(1)解：$\because \angle C = 90^{\circ}$，$AB = 10cm$，$BC = 6cm$，$\therefore$由勾股定理得$AC = 8cm$，$\because$动点 P 从点 C 开始，按$C\rightarrow A\rightarrow B\rightarrow C$的路径运动，且速度为每秒 1cm，$\therefore$出发 2 秒后，则$CP = 2cm$，那么$AP = 6cm$。$\because \angle C = 90^{\circ}$，$\therefore$由勾股定理得$PB = 2\sqrt{10}cm$，$\therefore \triangle ABP$的周长为：$AP + PB + AB = 6 + 2\sqrt{10}+10=(16 + 2\sqrt{10})cm$；
(2)如图所示 ，过点 P 作$PD\perp AB$于点 D，连接 BP，$\because BP$平分$\angle ABC$，$\therefore PD = PC$。在$Rt\triangle BPD$与$Rt\triangle BPC$中，$\begin{cases}PD = PC\\BP = BP\end{cases}$，$\therefore Rt\triangle BPD\cong Rt\triangle BPC(HL)$，$\therefore BD = BC = 6cm$，$\therefore AD = 10 - 6 = 4(cm)$。设$PC = x cm$，则$PA=(8 - x)cm$，在$Rt\triangle APD$中，$PD^{2}+AD^{2}=PA^{2}$，即$x^{2}+4^{2}=(8 - x)^{2}$，解得$x = 3$，$\therefore$当$t = 3$秒时，$BP$平分$\angle ABC$；
(3)若 P 在边 AC 上时，$BC = CP = 6cm$，此时用的时间为 6s，故$t = 6s$时，$\triangle BCP$为等腰三角形；若 P 在 AB 边上时，有三种情况：①若使$BP = BC = 6cm$，此时$AP = 4cm$，P 运动的路程为 12cm，此时用的时间为 12s，故$t = 12s$时，$\triangle BCP$为等腰三角形；②若$CP = BC = 6cm$，过 C 作斜边 AB 的高，根据面积法求得高为 4.8cm，根据勾股定理求得$BP = 7.2cm$，所以 P 运动的路程为$18 - 7.2 = 10.8(cm)$，此时用的时间为 10.8s，故$t = 10.8s$时，$\triangle BCP$为等腰三角形；③若$BP = CP$时，则$\angle PCB = \angle PBC$，$\because \angle ACP+\angle BCP = 90^{\circ}$，$\angle PBC+\angle CAP = 90^{\circ}$，$\therefore \angle ACP = \angle CAP$，$\therefore PA = PC$，$\therefore PA = PB = 5cm$。$\therefore P$运动的路程为 13cm，此时用的时间为 13s，故$t = 13s$时，$\triangle BCP$为等腰三角形。$\therefore t = 6s$或 13s 或 12s 或 10.8s 时，$\triangle BCP$为等腰三角形。