《2025年课堂点睛八年级数学下册人教版安徽专版》

八(本大题满分14分)
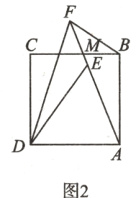
23. 如图,点M是正方形ABCD的边BC上一点,连接AM,点E是线段AM上一点,∠CDE的平分线交AM延长线于点F.
(1)如图1,若点E为线段AM的中点,BM∶CM = 1∶2,BE = $\sqrt{10}$,求AB的长;(6分)
(2)如图2,若DA = DE,求证:BF + DF = $\sqrt{2}$AF.(8分)

答案：

(1)解：设$BM = x$，则$CM = 2x,BC = 3x,\because BA = BC,\therefore BA = 3x$。在$Rt\triangle ABM$中，E为斜边AM中点，$\therefore AM = 2BE = 2\sqrt{10}$。由勾股定理可得$AM^{2}=MB^{2}+AB^{2}$，即$40 = x^{2}+9x^{2}$，解得$x = 2.\therefore AB = 3x = 6$。
(2)如图2 ，延长FD交过点A作垂直于AF的直线于H点，过点D作$DP\perp AF$于P点。$\because DF$平分$\angle CDE,\therefore\angle1=\angle2.\because DE = DA,DP\perp AF,\therefore\angle3=\angle4$。$\because\angle1+\angle2+\angle3+\angle4 = 90^{\circ},\therefore\angle2+\angle3 = 45^{\circ}.\therefore\angle DFP = 90^{\circ}-45^{\circ}=45^{\circ}.\therefore AH = AF$。$\because\angle BAF+\angle DAF = 90^{\circ},\angle HAD+\angle DAF = 90^{\circ},\therefore\angle BAF=\angle DAH$。又$AB = AD,\therefore\triangle ABF\cong\triangle ADH(SAS).\therefore BF = DH$。$\because Rt\triangle FAH$是等腰直角三角形，$\therefore HF=\sqrt{2}AF$。$\because HF = DH + DF = BF + DF,\therefore BF + DF=\sqrt{2}AF$。