《2025年高考模拟试题汇编高中数学》

16. (15分)
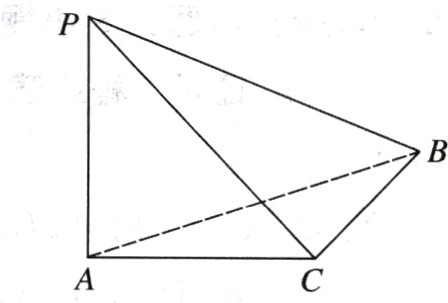
如图，已知三棱锥$P - ABC$中，平面$PAB\perp$底面$ABC$，$BC\perp$平面$PAC$，且$AC = BC = 2$，$PB = 2\sqrt{3}$.
(Ⅰ)求三棱锥$P - ABC$的体积；
(Ⅱ)已知$\overrightarrow{AD}=3\overrightarrow{AC}+2\overrightarrow{AP}$，求平面$PAB$与平面$BCD$所成二面角的正弦值.

答案： 空间中直线与平面的位置关系+三棱锥的体积+二面角的正弦值+空间向量的应用 解：(Ⅰ)取$AB$的中点$E$，连接$CE$，由$AC = BC$，$BC\perp$平面$PAC$，得$CE\perp AB$，$BC\perp PA$. （2 分）又平面$PAB\perp$底面$ABC$，平面$PAB\cap$底面$ABC = AB$，所以$CE\perp$平面$PAB$，（3 分）所以$CE\perp PA$，（4 分）又$CE\cap BC = C$，$CE$，$BC\subset$平面$ABC$，所以$PA\perp$底面$ABC$（提示：线面垂直的判定定理），（5 分）所以$PA\perp AC$. 因为$BC\perp$平面$PAC$，所以$BC\perp PC$，所以$PC = \sqrt{PB^2 - BC^2} = 2\sqrt{2}$，则$PA = \sqrt{PC^2 - AC^2} = 2$，从而三棱锥$P - ABC$的体积为$\frac{1}{3}\times\frac{1}{2}\times AC\times BC\times PA = \frac{4}{3}$. （6 分） (Ⅱ)由(Ⅰ)以$A$为坐标原点，过点$A$作$BC$的平行线为$y$轴，$AC$，$AP$所在直线分别为$x$，$z$轴，建立如图所示的空间直角坐标系（题眼），（7 分）有$A(0,0,0)$，$P(0,0,2)$，$C(2,0,0)$，$B(2,2,0)$，$E(1,1,0)$，所以$\overrightarrow{AC} = (2,0,0)$，$\overrightarrow{AP} = (0,0,2)$，$\overrightarrow{CB} = (0,2,0)$，（8 分）所以$\overrightarrow{AD} = (6,0,4)$，$\overrightarrow{BD} = (4,-2,4)$，（9 分）设平面$BCD$的法向量为$\boldsymbol{n} = (x,y,z)$，则$\begin{cases}\overrightarrow{BD}\cdot\boldsymbol{n} = 0\\\overrightarrow{CB}\cdot\boldsymbol{n} = 0\end{cases}$，即$\begin{cases}4x - 2y + 4z = 0\\2y = 0\end{cases}$，$y = 0$，取$x = 1$，得$z = -1$，所以$\boldsymbol{n} = (1,0,-1)$. （10 分）又易得平面$PAB$的一个法向量为$\overrightarrow{EC} = (1,-1,0)$，（12 分）则$\cos\langle\overrightarrow{EC},\boldsymbol{n}\rangle = \frac{\boldsymbol{n}\cdot\overrightarrow{EC}}{|\boldsymbol{n}||\overrightarrow{EC}|} = \frac{1}{2}$（提示：空间向量的夹角公式），（14 分）所以平面$PAB$与平面$BCD$所成二面角的正弦值为$\frac{\sqrt{3}}{2}$. （15 分）

17. (15分)
已知函数$f(x)=x^{3}+ax^{2}+bx + c(a,b,c\in R)$.
(Ⅰ)证明：函数$f(x)$有三个不同零点的必要条件是$a^{2}＞3b$；
(Ⅱ)由代数基本定理，$n$次复系数多项式方程在复数域内有且只有$n$个根(重根按重数计算).若$2a^{2}＜5b$，证明：方程$x^{2}f(x)+x - 1 = 0$至多有3个实数根.

答案： 方程的根与函数的零点+导数在研究函数中的应用 证明：(Ⅰ)$f'(x) = 3x^2 + 2ax + b$，令$f'(x) = 3x^2 + 2ax + b = 0$，其判别式$\Delta = 4a^2 - 12b = 4(a^2 - 3b)$. （2 分）若函数$f(x)$有三个不同零点，则$f(x)$必有极大值点与极小值点，（3 分）故$\Delta = 4(a^2 - 3b) > 0$，从而其必要条件为$a^2 > 3b$. （5 分） (Ⅱ)令$g(x) = x^2f(x) + x - 1 = x^5 + ax^4 + bx^3 + cx^2 + x - 1$. （6 分）令$h(x) = g'(x) = 5x^4 + 4ax^3 + 3bx^2 + 2cx + 1$，（7 分）令$p(x) = h'(x) = 20x^3 + 12ax^2 + 6bx + 2c$，（8 分）则$p'(x) = 60x^2 + 24ax + 6b$. （9 分）令$p'(x) = 0$，由$\Delta = (24a)^2 - 24\times60b = 12\times24(2a^2 - 5b) < 0$（题眼），可知$p'(x) > 0$，（10 分）所以$h'(x)$在定义域上单调递增，则其仅有唯一零点，不妨记为$x_0$，可知在$(-\infty,x_0)$上，$h'(x) < 0$，在$(x_0,+\infty)$上，$h'(x) > 0$，故$g'(x)$在定义域上先减后增，（12 分）所以$g'(x)$至多有两个不同的零点，不妨设为$x_1$，$x_2(x_1 < x_2)$，从而$g(x)$在$(-\infty,x_1)$上单调递增，在$(x_1,x_2)$上单调递减，在$(x_2,+\infty)$上单调递增，（13 分）从而$g(x)$至多有三个不同零点，（14 分）所以方程$x^2f(x) + x - 1 = 0$至多有 3 个实数根. （15 分）