《2025年高考模拟试题汇编高中数学》

16. （15分）
如图，三棱柱$ABC - A_{1}B_{1}C_{1}$中，四边形$ACC_{1}A_{1}$，$BCC_{1}B_{1}$均为正方形，$D$，$E$分别是棱$AB$，$A_{1}B_{1}$的中点，$N$为$C_{1}E$上一点.
（Ⅰ）证明：$BN//$平面$A_{1}DC$；
（Ⅱ）若$AB = AC$，$\overrightarrow{C_{1}E}=3\overrightarrow{C_{1}N}$，求直线$DN$与平面$A_{1}DC$所成角的正弦值.

答案：
16.空间中直线与平面间的位置关系+线面角+空间向量的应用
　　解:(I)证明:连接BE，BC1,DE.
　　　　　　　　
　　因为AB//AB1,且AB=A1B1,
　　又D,E分别是棱AB,A1B1的中点，
　　所以BD//AE,且BD=A1E,
　　所以四边形BDAlE为平行四边形，所以AlD/BE.
　　又AlDC平面ADC,BEC平面AlDC,
　　所以BE/平面ADC(提示:线面平行的判定定理).
　　因为DE/BB//CC,且DE=BB1=CC1,
　　所以四边形DCCE为平行四边形，所以ClE//CD.
　　又CDC平面ADC,ClEC平面ADC,
　　所以ClE/Z平面ADC.
　　因为CE∩BE=E,ClE,BEC平面BEC,
　　所以平面BEC1//平面ADC(提示:面面平行的判定定理).
　　因为BNC平面BEC1,所以BN/平面ADC(提示:利用面
　　面平行推出线面平行).　　　　　　　　　　　　　　(7分)
　　(II)因为四边形ACCA1,BCC!B均为正方形，
　　所以CC⊥AC,CC1⊥BC.
CCACC平面A直的判定定理).
知DE//CC,
　　所以DE⊥平面ABC.
　　从而DE⊥DB,DE⊥DC.
　　又AB=AC,AC=CC=BC,
　　所以△ABC为等边三角形.
　　因为D是棱AB的中点，
　　所以CD⊥DB，
　　即DB,DC,DE两两互相垂直.
以D为坐标原点，DB,DC,DE所在直线分别为x,y,N轴，建立如图所示的空间直角坐标系D一xyz.
　　　　　　
D(0,0,0),设AB=2$\sqrt{3}$,则E(0,0,2$\sqrt{3}$),C(0,3,0),
C1(0,3,2$\sqrt{3}$),A1(|　$\sqrt{3}$,0,2$\sqrt{3}$),
　所以DC=(0,3,0),DA=(|　$\sqrt{3}$,0,2$\sqrt{3}$).
　设平面ADC的法向量为n=(x,y,z),
　　n.DC=0,　　　3y=0,
　则{　　　　　　即{
　　n.DA²=0,　　$\sqrt{3}$x+2$\sqrt{3}$x=0,
　令x=1,则x=2,y=0,可得n=(2,0,1).
　因为CE=3CN,所以N(0,2,2$\sqrt{3}$),
　所以DN=(0,2,2$\sqrt{3}$).
　设直线DN与平面ADC所成角为0，
　则sinθ=|cos＜n,DN＞|=$\frac{n.DN|}{n|.|DN}$=$\frac{2\sqrt{3}}{5×4}$=$\frac{\sqrt{15}}{10}$,
　即直线DN与平面A,DC所成角的正弦值即直线DN与平面A,DC所成角的正弦值为.　(15分)
　注:其他解法酌情给分

17. （15分）
2023年9月26日，第十四届中国（合肥）国际园林博览会在合肥骆岗公园开幕. 本届园博会以“生态优先，百姓园博”为主题，共设有5个省内展园、26个省外展园和7个国际展园，开园面积近3.23平方公里. 游客可通过乘坐观光车、骑自行车和步行三种方式游园.
（Ⅰ）若游客甲计划在5个省内展园和7个国际展园中随机选择2个展园游玩，记甲参观省内展园的数量为$X$，求$X$的分布列及数学期望$E(X)$；
（Ⅱ）为更好地服务游客，主办方随机调查了500名首次游园且只选择一种游园方式的游客，其选择的游园方式和游园结果的统计数据如表：

用频率估计概率. 若游客乙首次游园，选择上述三种游园方式的一种，求游园结束时乙能参观完所有展园的概率.

答案：
17.离散型随机变量的分布列与数学期望+全概率公式
　解:(I)由题意知，X所有可能取值为0,1,2，且
　P(X=0)=$\frac{C’C²}{Ci2}$=$\frac{7}{22}$,
　P(X=1)=$\frac{CC}{C²2}$=$\frac{35}{66}$,
　P(X=2)=$\frac{C²C}{C²2}$=$\frac{5}{33}$,
　所以X的分布列为　　　　　　　　　　　　天利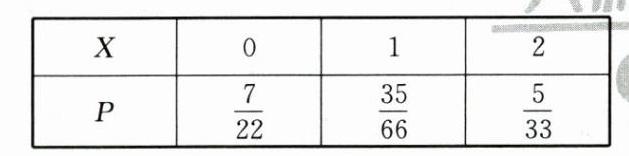
　所以X的数学期望E(X)=0×$\frac{7}{22}$+1×$\frac{35}{66}$+2×$\frac{5}{33}$
　　　　　　　　　　　　　　　　　　　　　(8分)
　(II)记事件A为“游客乙乘坐观光车游园”,事件B为“游客乙骑自行车游园”，事件C为“游客乙步行游园”，事件M为“游园结束时，乙能参观完所有展园”，
则P(A)=0.2,P(B)=0.4,P(C)=0.4,
　P(M|A)=0.8,P(M|B)=0.4,P(M|C)=0.2.
　由全概率公式,得P(M)=P(A)P(M|A)+P(B)P(M|B)+P(C)P(M|C)=0.2×0.8+0.4×0.4+0.4×0.2=0.4,
　所以游园结束时，乙能参观完所有展园的概率为0.4.(15分)