《2025年高考模拟试题汇编高中数学》

16. (15分)
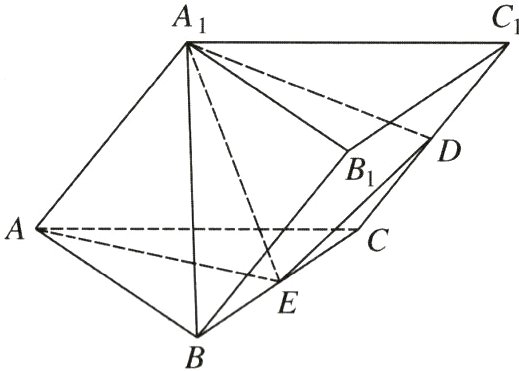
如图，三棱柱$ABC - A_{1}B_{1}C_{1}$的所有棱长都为3，点$A_{1}$在底面上的射影恰好是$\triangle ABC$的中心.
(Ⅰ)证明：四边形$BCC_{1}B_{1}$是正方形；
(Ⅱ)设$D$，$E$分别为$CC_{1}$，$BC$的中点，求二面角$A - A_{1}E - D$的正弦值.

答案：
棱柱的结构特征+空间中直线与平面的位置关系+二面角 解：(Ⅰ)证明：如图，设点$O$为$\triangle ABC$的中心，连接$A_{1}O$，易知点$O$在$AE$上，且$AE\perp BC$，$A_{1}O\perp$平面$ABC$. 因为$BC\subset$平面$ABC$， 所以$A_{1}O\perp BC$.(2 分) 又因为$A_{1}O\cap AE = O$，$A_{1}O$，$AE\subset$平面$AEA_{1}$， 所以$BC\perp$平面$AEA_{1}$(题眼).(4 分) 因为$AA_{1}\subset$平面$AEA_{1}$，所以$BC\perp AA_{1}$. 又因为$AA_{1}\parallel BB_{1}\parallel CC_{1}$， 所以$BC\perp BB_{1}$，且$BC\perp CC_{1}$， 又$BB_{1}=CC_{1}$， 所以四边形$BCC_{1}B_{1}$是矩形.(6 分) 因为$BC = BB_{1}$，所以矩形$BCC_{1}B_{1}$是正方形.(7 分) (Ⅱ)在线段$AB$上取点$F$，使得$\overrightarrow{AF}=2\overrightarrow{FB}$，连接$OF$，则$OF$，$OE$，$OA_{1}$两两垂直， 故以$O$为坐标原点，$\overrightarrow{OF}$，$\overrightarrow{OE}$，$\overrightarrow{OA_{1}}$的方向分别为$x$轴、$y$轴和$z$轴的正方向建立空间直角坐标系，如图所示(题眼)， 则$A(0,-\sqrt{3},0)$，$A_{1}(0,0,\sqrt{6})$，$C(-\frac{3}{2},\frac{\sqrt{3}}{2},0)$，$D(-\frac{3}{2},\sqrt{3},\frac{\sqrt{6}}{2})$，$E(0,\frac{\sqrt{3}}{2},0)$， 所以$\overrightarrow{DA_{1}}=(\frac{3}{2},-\sqrt{3},\frac{\sqrt{6}}{2})$，$\overrightarrow{DE}=(\frac{3}{2},-\frac{\sqrt{3}}{2},-\frac{\sqrt{6}}{2})$， 由(Ⅰ)知，$BC\perp$平面$AEA_{1}$，则平面$AEA_{1}$的一个法向量不妨取$\boldsymbol{m}=(1,0,0)$， 设平面$A_{1}ED$的法向量为$\boldsymbol{n}=(x,y,z)$， 则有$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{DA_{1}}=0\\\boldsymbol{n}\cdot\overrightarrow{DE}=0\end{cases}$，即$\begin{cases}\frac{3}{2}x-\sqrt{3}y+\frac{\sqrt{6}}{2}z = 0\\\frac{3}{2}x-\frac{\sqrt{3}}{2}y-\frac{\sqrt{6}}{2}z = 0\end{cases}$，(11 分) 取$y = 1$，则$\boldsymbol{n}=(\frac{\sqrt{3}}{2},1,\frac{\sqrt{2}}{4})$，(13 分) 所以$\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle=\frac{\boldsymbol{m}\cdot\boldsymbol{n}}{\vert\boldsymbol{m}\vert\vert\boldsymbol{n}\vert}=\frac{\sqrt{10}}{5}$， 故二面角$A - A_{1}E - D$的正弦值为$\frac{\sqrt{15}}{5}$.(15 分) 

17. (15分)
某同学进行投篮训练，已知每次投篮的命中率均为0.5.
(Ⅰ)若该同学共投篮4次，求在投中2次的条件下，第二次没有投中的概率；
(Ⅱ)设随机变量$\xi$服从二项分布$B(n,p)$，记$\eta=\frac{\xi - np}{\sqrt{np(1 - p)}}$，则当$n\geqslant20$时，可认为$\eta$服从标准正态分布$N(0,1)$.若保证投中的频率在区间$[0.4,0.6]$的概率不低于90%，求该同学至少要投多少次.
附：若$\eta\sim N(0,1)$，则$P(\eta＜1.28)=0.9$，$P(\eta＜1.645)=0.95$.

答案： 条件概率+二项分布+正态分布 解：(Ⅰ)设事件$A_{n}$表示共有$n(n = 0,1,2,3,4)$次投中，事件$B$表示第二次没有投中， 则$P(BA_{2})=\frac{1}{2}\times C_{3}^{2}\times\frac{1}{2^{2}}\times\frac{1}{2}=\frac{3}{16}$，(2 分) $P(A_{2})=C_{4}^{2}\times\frac{1}{2^{2}}\times\frac{1}{2^{2}}=\frac{3}{8}$，(4 分) 所以$P(B|A_{2})=\frac{P(BA_{2})}{P(A_{2})}=\frac{\frac{3}{16}}{\frac{3}{8}}=\frac{1}{2}$.(6 分) (Ⅱ)设至少投$n$次，其中投中的次数$\xi\sim B(n,0.5)$， 若$P(0.4\leq\frac{\xi}{n}<0.6)\geq0.9$， 即$P(0.4n\leq\xi<0.6n)\geq0.9$，(8 分) 即$P(\frac{-0.1n}{0.5\sqrt{n}}\leq\frac{\xi - 0.5n}{0.5\sqrt{n}}<\frac{0.1n}{0.5\sqrt{n}})\geq0.9$，由已知条件可得$P(-0.2\sqrt{n}\leq\eta<0.2\sqrt{n})\geq0.9$(题眼)(方法：将频率不等式转化为关于$\xi$的不等式，再转化为关于$\eta$的不等式，从而转化为正态分布问题).(12 分) 又因为$P(\eta<1.645)=0.95$， 所以$0.2\sqrt{n}\geq1.645$，解得$n>67.65$， 所以至少要投 68 次才能保证投中的频率在区间$[0.4,0.6)$的概率不低于 90%.(15 分)