《2025年高考模拟试题汇编高中数学》

18. (17分)
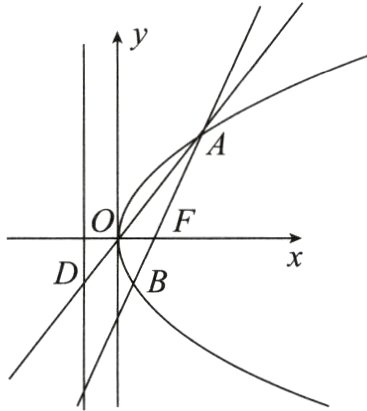
如图，$O$为坐标原点，$F$为抛物线$y^{2}=2x$的焦点，过点$F$的直线交抛物线于$A$，$B$两点，直线$AO$交抛物线的准线于点$D$，设抛物线在$B$点处的切线为$l$.
(Ⅰ)若直线$l$与$y$轴的交点为$E$，求证：$|DE| = |EF|$；
(Ⅱ)过点$B$作$l$的垂线与直线$AO$交于点$G$，求证：$|AD|^{2}=|AO|\cdot|AG|$.

答案：  直线与抛物线的位置关系+导数的几何意义+平行线的性质 【思维导图】(Ⅰ)已知条件→设直线$AB:x = my+\frac{1}{2}$与抛物线方程联立$\begin{cases}\Delta\gt0\\y_{1}+y_{2}\\y_{1}y_{2}\end{cases}\xrightarrow{导数的几何意义}$$l$的斜率→$l$的方程→点$E$的坐标→直线$OA$的方程→点$D$的坐标→$\overrightarrow{DE}=\overrightarrow{EF}$→得证. (Ⅱ)证法一：已知条件→过点$B$的$l$的垂线的方程联立方程→$y_{G}$→$|y_{2}-y_{1}|^{2}=|y_{1}|\cdot|y_{G}-y_{1}|$→得证； 证法二：已知条件→$DB\parallel x$轴$\xrightarrow{平行线的性质}$$\frac{|AF|}{|AB|}=\frac{|AO|}{|AD|}$同理$\frac{|AF|}{|AB|}=\frac{|AD|}{|AG|}$→得证. 证明：(Ⅰ)设直线$AB$的方程为$x = my+\frac{1}{2}$，$A(x_{1},y_{1})$，$B(x_{2},y_{2})$，(1分) 联立$\begin{cases}x = my+\frac{1}{2}\\y^{2}=2x\end{cases}$，消去$x$整理得$y^{2}-2my - 1=0$（题眼），(2分) $\therefore\begin{cases}\Delta\gt0\\y_{1}+y_{2}=2m\\y_{1}y_{2}=-1\end{cases}$.(3分) 不妨设点$A$在第一象限，点$B$在第四象限，对于$y = -\sqrt{2x}$，$y^{\prime}=-\frac{1}{\sqrt{2x}}$，(4分) $\therefore l$的斜率为$-\frac{1}{\sqrt{2x_{2}}}=-\frac{1}{\sqrt{y_{2}^{2}}}=\frac{1}{y_{2}}$（提示：导数的几何意义），(5分) $\therefore l$的方程为$y - y_{2}=\frac{1}{y_{2}}(x - x_{2})$，即$y=\frac{1}{y_{2}}x+\frac{y_{2}}{2}$，(6分) 令$x = 0$，得$E(0,\frac{y_{2}}{2})$.(7分) 直线$OA$的方程为$y=\frac{y_{1}}{x_{1}}x=\frac{2}{y_{1}}x=-2y_{2}x$，令$x = -\frac{1}{2}$，得$D(-\frac{1}{2},y_{2})$.(8分) 又$F(\frac{1}{2},0)$，$\therefore\overrightarrow{DE}=\overrightarrow{EF}$，即$|DE| = |EF|$，得证（提示：相等向量的模长相等）.(10分) (Ⅱ)证法一：过点$B$的$l$的垂线的方程为$y - y_{2}=-y_{2}(x - x_{2})$（题眼），即$y=-y_{2}x+y_{2}(1+\frac{y_{2}^{2}}{2})$，(11分) 联立$\begin{cases}y=-y_{2}x+y_{2}(1+\frac{y_{2}^{2}}{2})\\y=-2y_{2}x\end{cases}$，解得$y_{G}=y_{2}(2 + y_{2}^{2})$.(13分) 要证明$|AD|^{2}=|AO|\cdot|AG|$，因为$A$，$O$，$D$，$G$四点共线，所以只需证明：$|y_{2}-y_{1}|^{2}=|y_{1}|\cdot|y_{G}-y_{1}|$.(*) (14分) $\because|y_{2}-y_{1}|^{2}=|y_{2}+\frac{1}{y_{2}}|^{2}=\frac{(y_{2}^{2}+1)^{2}}{y_{2}^{2}}$，$|y_{1}|\cdot|y_{G}-y_{1}|=|-\frac{1}{y_{2}}||y_{2}(2 + y_{2}^{2})+\frac{1}{y_{2}}|=\frac{(y_{2}^{2}+1)^{2}}{y_{2}^{2}}$，(15分)(16分) $\therefore(*)$成立，即$|AD|^{2}=|AO|\cdot|AG|$得证.(17分) 证法二：由$D(-\frac{1}{2},y_{2})$，$B(x_{2},y_{2})$知，$DB\parallel x$轴，(12分) $\therefore\frac{|AF|}{|AB|}=\frac{|AO|}{|AD|}$.①(13分) 又$DF$的斜率为$-y_{2}$，$BG$的斜率为$-y_{2}$，$\therefore DF\parallel BG$，(15分) $\therefore\frac{|AF|}{|AB|}=\frac{|AD|}{|AG|}$.②(16分) 由①②得$\frac{|AO|}{|AD|}=\frac{|AD|}{|AG|}$（题眼），即$|AD|^{2}=|AO|\cdot|AG|$得证.(17分)

19. (17分)
微积分的创立是数学发展中的里程碑，它的发展和广泛应用开创了向近代数学过渡的新时期，为研究变量和函数提供了重要的方法和手段. 对于函数$f(x)=\frac{1}{x}(x\gt0)$，$f(x)$在区间$[a,b]$上的图象连续不断，从几何上看，定积分$\int_{a}^{b}\frac{1}{x}dx$便是由直线$x = a$，$x = b$，$y = 0$和曲线$y=\frac{1}{x}$所围成的区域(称为曲边梯形$ABQP$)的面积，根据微积分基本定理可得$\int_{a}^{b}\frac{1}{x}dx=\ln b-\ln a$，因为曲边梯形$ABQP$的面积小于梯形$ABQP$的面积，即$S_{曲边梯形ABQP}\lt S_{梯形ABQP}$，代入数据，进一步可以推导出不等式：$\frac{a - b}{\ln a-\ln b}\gt\frac{2}{\frac{1}{a}+\frac{1}{b}}$.
(Ⅰ)请仿照这种根据面积关系证明不等式的方法，证明：$\frac{a - b}{\ln a-\ln b}\lt\frac{a + b}{2}$；
(Ⅱ)已知函数$f(x)=ax^{2}+bx+x\ln x$，其中$a$，$b\in R$.
(ⅰ)证明：对任意两个不相等的正数$x_{1}$，$x_{2}$，曲线$y = f(x)$在$(x_{1},f(x_{1}))$和$(x_{2},f(x_{2}))$处的切线均不重合；
(ⅱ)当$b = -1$时，若不等式$f(x)\geq2\sin(x - 1)$恒成立，求实数$a$的取值范围.

答案： 函数与导数的综合应用 【思维导图】(Ⅰ)已知条件→在曲线$y=\frac{1}{x}$上取一点$M(\frac{a + b}{2},\frac{2}{a + b})$$S_{曲边梯形ABQP}\gt S_{梯形ABM_{2}M_{1}}\xrightarrow{}$$\ln b-\ln a\gt\frac{1}{2}(|AM_{1}|+|BM_{2}|)\cdot|AB|$→得证. (Ⅱ)(ⅰ)证法一：已知条件→$f^{\prime}(x)$$\xrightarrow{导数的几何意义、切线的方程}$$l_{1}$，$l_{2}$假设$l_{1}$，$l_{2}$重合$\xrightarrow{}$$\frac{x_{2}-x_{1}}{\ln x_{2}-\ln x_{1}}=\frac{x_{2}+x_{1}}{2}$→矛盾→得证； 证法二：已知条件$\xrightarrow{同证法一}$$\ln\frac{x_{2}}{x_{1}}-2\frac{\frac{x_{2}}{x_{1}}-1}{\frac{x_{2}}{x_{1}}+1}=0$令$t=\frac{x_{2}}{x_{1}}(t\gt1)$$\xrightarrow{}$$g(t)=\ln t-2\frac{t - 1}{t + 1}$$\xrightarrow{g^{\prime}(t)}$$g(t)\gt0$→矛盾→得证. (ⅱ)已知条件→令$h(x)=f(x)-2\sin(x - 1)$→$h(x)\geqslant0$→$h(1)\geqslant0$→$a\geqslant1$$\xrightarrow{分x\in[1,+\infty)和x\in(0,1)讨论}$证明当$a\geqslant1$时，$h(x)\geqslant0$恒成立→$a$的取值范围. 解：(Ⅰ)证明：在曲线$y=\frac{1}{x}$上取一点$M(\frac{a + b}{2},\frac{2}{a + b})$，(1分) 过点$M(\frac{a + b}{2},\frac{2}{a + b})$作$f(x)$的切线分别交$AP$，$BQ$于点$M_{1}$，$M_{2}$.(2分) $\because S_{曲边梯形ABQP}\gt S_{梯形ABM_{2}M_{1}}$（题眼），(3分) $\therefore\ln b-\ln a\gt\frac{1}{2}\cdot(|AM_{1}|+|BM_{2}|)\cdot|AB|=\frac{1}{2}\times2\cdot\frac{2}{a + b}\cdot(b - a)$，(4分) 即$\frac{a - b}{\ln a-\ln b}\lt\frac{a + b}{2}$.(5分) (Ⅱ)(ⅰ)证法一：由题意得$f^{\prime}(x)=2ax+\ln x+b + 1$（题眼）. 不妨设$0\lt x_{1}\lt x_{2}$，曲线$y = f(x)$在$(x_{1},f(x_{1}))$处的切线方程$l_{1}:y - f(x_{1})=f^{\prime}(x_{1})(x - x_{1})$，即$y=f^{\prime}(x_{1})x+f(x_{1})-x_{1}f^{\prime}(x_{1})$（提示：导数的几何意义与切线的方程）.(6分) 同理曲线$y = f(x)$在$(x_{2},f(x_{2}))$处的切线方程$l_{2}:y=f^{\prime}(x_{2})x+f(x_{2})-x_{2}f^{\prime}(x_{2})$，(7分) 假设$l_{1}$与$l_{2}$重合，则$\begin{cases}f^{\prime}(x_{1})=f^{\prime}(x_{2})\\f(x_{1})-x_{1}f^{\prime}(x_{1})=f(x_{2})-x_{2}f^{\prime}(x_{2})\end{cases}$，代入化简可得$\begin{cases}\ln x_{2}-\ln x_{1}+2a(x_{2}-x_{1})=0\\a(x_{2}+x_{1})=-1(a\lt0)\end{cases}$，(8分) 两式消去$a$可得$\ln x_{2}-\ln x_{1}-2\frac{x_{2}-x_{1}}{x_{2}+x_{1}}=0$，得到$\frac{x_{2}-x_{1}}{\ln x_{2}-\ln x_{1}}=\frac{x_{2}+x_{1}}{2}$.(9分) 由(Ⅰ)的结论知$\frac{x_{2}-x_{1}}{\ln x_{2}-\ln x_{1}}\lt\frac{x_{2}+x_{1}}{2}$，与上式矛盾，(10分) 故对任意实数$a$，$b$及任意两个不相等的正数$x_{1}$，$x_{2}$，曲线$y = f(x)$在$(x_{1},f(x_{1}))$和$(x_{2},f(x_{2}))$处的切线均不重合.(11分) 证法二：同证法一得到$\ln\frac{x_{2}}{x_{1}}-2\frac{\frac{x_{2}}{x_{1}}-1}{\frac{x_{2}}{x_{1}}+1}=0$.(9分) 令$t=\frac{x_{2}}{x_{1}}(t\gt1)$，$g(t)=\ln t-2\frac{t - 1}{t + 1}$，$g^{\prime}(t)=\frac{1}{t}-\frac{4}{(t + 1)^{2}}=\frac{(t - 1)^{2}}{t(t + 1)^{2}}\gt0$，(10分) $\therefore g(t)$在$(1,+\infty)$上为增函数，$\therefore g(t)\gt g(1)=0$，矛盾， 故对任意实数$a$，$b$及任意两个不相等的正数$x_{1}$，$x_{2}$，曲线$y = f(x)$在$(x_{1},f(x_{1}))$和$(x_{2},f(x_{2}))$处的切线均不重合.(11分) (ⅱ)当$b=-1$时，不等式$f(x)\geqslant2\sin(x - 1)$恒成立（题眼），即$ax^{2}-x+x\ln x-2\sin(x - 1)\geqslant0$恒成立， 令$h(x)=ax^{2}-x+x\ln x-2\sin(x - 1)$，则$h(x)\geqslant0$在$(0,+\infty)$上恒成立，$\therefore h(1)\geqslant0\Rightarrow a\geqslant1$.(12分) 下证：当$a\geqslant1$时，$h(x)\geqslant0$恒成立. $\because a\geqslant1$，所以$h(x)\geqslant x^{2}-x+x\ln x-2\sin(x - 1)$，(13分) 令$H(x)=x^{2}-x+x\ln x-2\sin(x - 1)$，$H^{\prime}(x)=2x+\ln x-2\cos(x - 1)$， ①当$x\in[1,+\infty)$时，由$2x\geqslant2$，$\ln x\geqslant0$，$-2\cos(x - 1)\geqslant-2$，知$H^{\prime}(x)\geqslant0$恒成立，即$H(x)$在$[1,+\infty)$上为增函数，$\therefore H(x)\geqslant H(1)=0$成立；(14分) ②当$x\in(0,1)$时，令$G(x)=2x+\ln x-2\cos(x - 1)$，$G^{\prime}(x)=2+\frac{1}{x}+2\sin(x - 1)$， 由$2\sin(x - 1)\geqslant-2$，$\frac{1}{x}\gt0$，知$G^{\prime}(x)\geqslant0$恒成立，即$G(x)=H^{\prime}(x)$在$(0,1)$上为增函数，$\therefore H^{\prime}(x)\lt H^{\prime}(1)=0$，即$H(x)$在$(0,1)$上为减函数，$\therefore H(x)\gt H(1)=0$成立. 综上所述，实数$a$的取值范围是$[1,+\infty)$.(17分) （解析人：杜 伟）