《2025年高考模拟试题汇编高中数学》

1. 已知集合$M = \{ x|x^{2}+3x - 10\lt0\}$，$N = \{ y|y = \sqrt{x - 1}\}$，则$M\cap N =$( )
A. $[0,2)$
B. $[1,2)$
C. $[-5,2)$
D. $(-5,2)$

答案： A

2. 已知$i$为虚数单位，复数$z$满足$|z + 2i| = |z|$，则$\overline{z}$的虚部为( )
A. $-1$
B. $1$
C. $i$
D. $-i$

答案： B

3. 若$\tan(\alpha - \frac{\pi}{4}) = 2$，则$\sin2\alpha =$( )
A. $\frac{3}{5}$
B. $-\frac{3}{5}$
C. $\frac{4}{5}$
D. $-\frac{4}{5}$

答案： B

4. 已知向量$\boldsymbol{a}$，$\boldsymbol{b}$，满足$|\boldsymbol{a}| = |\boldsymbol{b}| = |\boldsymbol{a} - \boldsymbol{b}|$，则$\boldsymbol{a}\cdot(\boldsymbol{a} + \boldsymbol{b}) =$( )
A. $\frac{1}{2}\boldsymbol{a}^{2}$
B. $\frac{1}{2}\boldsymbol{b}^{2}$
C. $\frac{1}{2}(\boldsymbol{a} + \boldsymbol{b})^{2}$
D. $\frac{1}{2}(\boldsymbol{a} - \boldsymbol{b})^{2}$

答案： C

5. 如图，$A$是平面$\alpha$内一定点，$B$是平面$\alpha$外一定点，且$AB = 4\sqrt{2}$，直线$AB$与平面$\alpha$所成角为$45^{\circ}$，设平面$\alpha$内动点$M$到点$A$，$B$的距离相等，则线段$AM$的最小值为( )

A. $4$
B. $2\sqrt{2}$
C. $2$
D. $\frac{\sqrt{2}}{2}$

答案： A

6. $(x^{2}+ax - 1)\cdot(1 - x)^{6}$的展开式中$x^{2}$的系数是$-2$，则实数$a$的值为( )
A. $0$
B. $3$
C. $-1$
D. $-2$

答案： B

7. 平面直角坐标系$xOy$中，已知点$A(-a,0)$，$B(a,0)$，其中$a\gt0$，若圆$(x - a + 1)^{2}+(y - a - 2)^{2}=a^{2}$上存在点$P$满足$\overrightarrow{PA}\cdot\overrightarrow{PB}=3a^{2}$，则实数$a$的取值范围是( )
A. $(0,\frac{1}{2}]$
B. $[\frac{1}{2},1]$
C. $[\frac{1}{2},+\infty)$
D. $[1,+\infty)$

答案： B

8. 若对于任意正数$x$，$y$，不等式$x(1 + \ln x)\geqslant x\ln y - ay$恒成立，则实数$a$的取值范围是( )
A. $(0,\frac{1}{e}]$
B. $[\frac{1}{e^{3}},\frac{1}{e}]$
C. $[\frac{1}{e^{2}},+\infty)$
D. $[\frac{1}{e^{3}},+\infty)$

答案： C

9. 若$X\sim N(100,1.5^{2})$，则下列说法正确的有( )
A. $P(X\lt100)=\frac{1}{2}$
B. $E(X)=1.5$
C. $P(X\lt101.5)=P(X\gt98.5)$
D. $P(97\lt X\lt101.5)=P(98.5\lt X\lt103)$

答案： AC

10. 如图所示的数阵的特点是：每行每列都成等差数列，该数列一共有$n$行$n$列$(n\geqslant100)$，$a_{ij}$表示第$i$行第$j$列的数，比如$a_{23}=7$，$a_{54}=21$，则( )

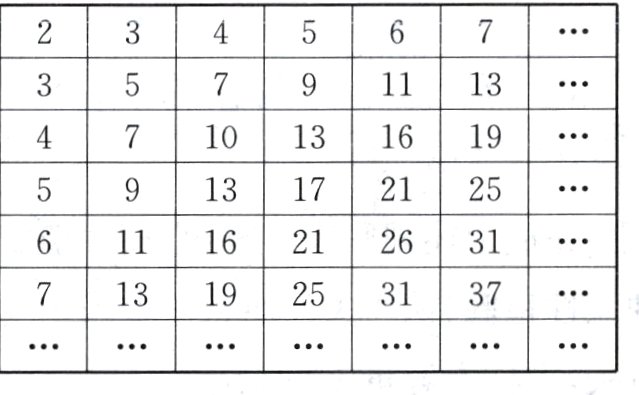
A. $a_{77}=50$
B. 数字65在这个数阵中出现的次数为8次
C. $a_{ij}=i\cdot j + 1$
D. 这个数阵中$n^{2}$个数的和$S=\frac{n^{2}(n + 1)^{2}}{4}$

答案： ABCD