《2025年高考模拟试题汇编高中数学》

16.(15分)
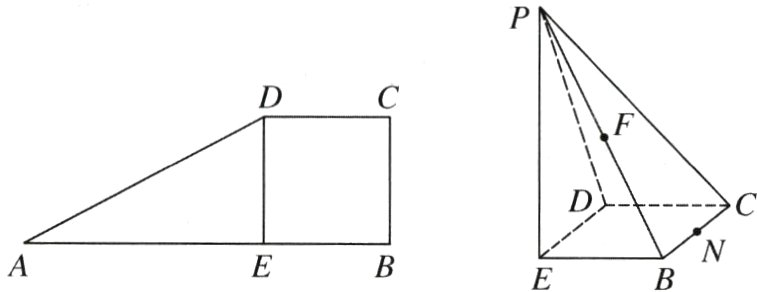
　如图,在直角梯形ABCD中,AB//CD,∠ABC=
　90°,AB=3DC=3BC,DE⊥AB于E,沿DE将△ADE折起,使得点A到点P位置,∠PEB=
　90°,N是棱BC上的动点(与点B,C不重合).(I)判断在棱PB上是否存在一点M,使平面EMN⊥平面PBC？若存在,求$\frac{BM}{BP}$;若不存在，说明理由;
　(II)当点F,N分别是PB,BC的中点时,求平面EFN和平面PDE的夹角的余弦值.
　　　

答案：  线面垂直的判定定理 + 面面垂直的判定定理与性质定理 + 平面与平面的夹角 解：（Ⅰ）存在. （1 分） 在四棱锥$P - EBCD$中，$PE\perp DE$，$PE\perp EB$， 又$DE\cap EB = E$，$DE$，$EB\subset$平面$BCDE$， $\therefore PE\perp$平面$BCDE$（题眼）. （2 分） $\because PE\subset$平面$PEB$， $\therefore$平面$PEB\perp$平面$BCDE$（提示：面面垂直的判定定理）. $\because BC\perp BE$，平面$PEB\cap$平面$BCDE = BE$， $\therefore BC\perp$平面$PEB$（提示：面面垂直的性质定理）， 又$BC\subset$平面$PBC$，$\therefore$平面$PEB\perp$平面$PBC$. （4 分） 过$E$作$EM\perp PB$交$PB$于$M$，连接$MN$， 又$\because$平面$PEB\cap$平面$PBC = PB$，$EM\subset$平面$PEB$， $\therefore EM\perp$平面$PBC$，$\therefore$平面$EMN\perp$平面$PBC$. （6 分） 在$Rt\triangle PEB$中，$EM\perp PB$， $\therefore PE^{2} = PM\cdot PB$，$BE^{2} = BM\cdot BP$，且$PE = 2BE$， $\therefore PM = 4BM$， $\therefore$在棱$PB$上存在点$M$，使平面$EMN\perp$平面$PBC$， 此时$\frac{BM}{BP} = \frac{1}{5}$. （7 分） （Ⅱ）以$E$为坐标原点，$EB$，$ED$，$EP$所在直线分别为$x$，$y$，$z$轴建立空间直角坐标系（题眼）， 设$BC = BE = 2$，则$PE = 4$， 则$E(0,0,0)$，$N(2,1,0)$，$B(2,0,0)$，$P(0,0,4)$，$F(1,0,2)$， $\overrightarrow{EN} = (2,1,0)$，$\overrightarrow{EF} = (1,0,2)$， （9 分） 设平面$EFN$的法向量为$\boldsymbol{n}_{1} = (x_{1},y_{1},z_{1})$， 由$\begin{cases}\overrightarrow{EN}\cdot\boldsymbol{n}_{1} = 0\\\overrightarrow{EF}\cdot\boldsymbol{n}_{1} = 0\end{cases}$，得$\boldsymbol{n}_{1} = (2,-4,-1)$. （11 分） 又易知平面$PDE$的一个法向量为$\boldsymbol{n}_{2} = (1,0,0)$， （13 分） 设平面$EFN$和平面$PDE$的夹角为$\theta$， $\therefore \cos\theta = |\cos\langle\boldsymbol{n}_{1},\boldsymbol{n}_{2}\rangle| = \frac{2}{\sqrt{21}} = \frac{2\sqrt{21}}{21}$， 则平面$EFN$和平面$PDE$的夹角的余弦值为$\frac{2\sqrt{21}}{21}$. （15 分） 

17.(15分)
　已知等比数列{a，}的前n项和为S，,且Sn+1=
　3S,+1,其中n∈N+.
　(I)求数列{a，}的通项公式;
　(II)在a，与an+1之间插入n个数,使这n+2个数组成一个公差为d，的等差数列,在数列{d，}中是否存在不同三项dm,dk,dp(其中m,k,p 成等差数列)成等比数列？若存在,求出这样的三项;若不存在,请说明理由.

答案： 等比数列的通项公式与性质 + 等差数列的性质 解：（Ⅰ）当$n\geq 2$时，$S_{n + 1} = 3S_{n} + 1$，$S_{n} = 3S_{n - 1} + 1$， 两式相减得$a_{n + 1} = 3a_{n}(n\geq 2)$（题眼）. （2 分） 又因为$\{ a_{n}\}$是等比数列，所以公比为 3. 由$S_{n + 1} = 3S_{n} + 1$知，当$n = 1$时，$a_{1} + a_{2} = 3a_{1} + 1$， 即$a_{2} = 2a_{1} + 1$. 因为$a_{2} = 2a_{1} + 1 = 3a_{1}$，故$a_{1} = 1$， 所以$a_{n} = 3^{n - 1}(n\in N_{+})$. （6 分） （Ⅱ）不存在. 理由如下： 由（Ⅰ）可知$a_{n} = 3^{n - 1}$，$a_{n + 1} = 3^{n}$. 因为$a_{n + 1} = a_{n} + (n + 2 - 1)d_{n}$， 所以$d_{n} = \frac{2\cdot 3^{n - 1}}{n + 1}$（题眼）， （8 分） 假设在数列$\{ d_{n}\}$中存在不同三项$d_{m}$，$d_{k}$，$d_{p}$（其中$m$，$k$，$p$成等差数列）成等比数列， 则$(d_{k})^{2} = d_{m}\cdot d_{p}$， 即$(\frac{2\cdot 3^{k - 1}}{k + 1})^{2} = \frac{2\cdot 3^{m - 1}}{m + 1}\cdot\frac{2\cdot 3^{p - 1}}{p + 1}$（提示：等比数列的性质）， （10 分） 所以$\frac{4\cdot 3^{2k - 2}}{(k + 1)^{2}} = \frac{4\cdot 3^{m + p - 2}}{(m + 1)(p + 1)}$. （*） 因为$m$，$k$，$p$成等差数列， 所以$m + p = 2k$（提示：等差数列的性质）， 代入上式整理可以得到$(k + 1)^{2} = (m + 1)(p + 1)$， （12 分） 即$k^{2} + 2k + 1 = mp + m + p + 1$，即$k^{2} = mp$， 即$(\frac{m + p}{2})^{2} = mp$，所以$(m - p)^{2} = 0$， 所以$m = k = p$，与题设矛盾， 所以在数列$\{ d_{n}\}$中不存在不同三项$d_{m}$，$d_{k}$，$d_{p}$（其中$m$，$k$，$p$成等差数列）成等比数列. （15 分）