《2025年高考模拟试题汇编高中数学》

16. (15分)
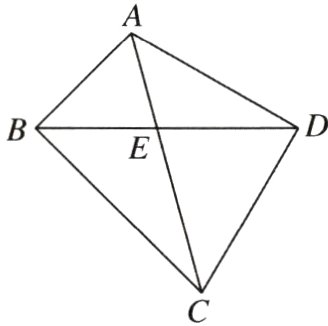
如图，两块直角三角形模具斜边靠在一起，其中公共斜边$AC = 10$，$\angle BAC = \frac{\pi}{3}$，$\angle DAC = \frac{\pi}{4}$，$BD$交$AC$于点$E$.
(Ⅰ)求$BD^{2}$；
(Ⅱ)求$AE$.

答案： 三角恒等变换 + 余弦定理 + 三角形面积公式 【思维导图】(Ⅰ)已知条件$\to AB$，$AD\xrightarrow{\angle BAD=\frac{\pi}{3}+\frac{\pi}{4}}\cos\angle BAD\xrightarrow{余弦定理}BD^{2}$. (Ⅱ)解法一：$S_{\triangle ABD}=S_{\triangle ABE}+S_{\triangle ADE}\xrightarrow{三角形面积公式}AE$； 解法二：$\frac{AE}{EC}=\frac{S_{\triangle ABD}}{S_{\triangle BCD}}\to EC=\sqrt{3}AE\xrightarrow{AC = 10}AE + EC = 10\to AE$. 解：(Ⅰ)由已知得$AB = AC\cdot\cos\angle BAC=10\times\frac{1}{2}=5$， $AD = AC\cdot\cos\angle DAC=10\times\frac{\sqrt{2}}{2}=5\sqrt{2}$. （2 分） 因为$\angle BAD=\angle BAC+\angle DAC=\frac{\pi}{3}+\frac{\pi}{4}$， 所以$\cos\angle BAD=\cos\frac{\pi}{3}\cos\frac{\pi}{4}-\sin\frac{\pi}{3}\sin\frac{\pi}{4}$ $=\frac{1}{2}\times\frac{\sqrt{2}}{2}-\frac{\sqrt{3}}{2}\times\frac{\sqrt{2}}{2}$ $=\frac{\sqrt{2}-\sqrt{6}}{4}$， （4 分） 所以在$\triangle ABD$中， $BD^{2}=AB^{2}+AD^{2}-2AB\cdot AD\cdot\cos\angle BAD$（题眼） $=25 + 50-2\times5\times5\sqrt{2}\times\frac{\sqrt{2}-\sqrt{6}}{4}$ $=50 + 25\sqrt{3}$. （7 分） (Ⅱ)解法一：因为$\sin\angle BAD=\sin(\frac{\pi}{3}+\frac{\pi}{4})=\frac{\sqrt{6}+\sqrt{2}}{4}$， （9 分） $S_{\triangle ABD}=S_{\triangle ABE}+S_{\triangle ADE}$（提示：根据面积相等关系进行变换）， 所以$\frac{1}{2}AB\cdot AD\cdot\sin\angle BAD=\frac{1}{2}AB\cdot AE\cdot\sin\angle BAE+\frac{1}{2}AE\cdot AD\cdot\sin\angle EAD$， （12 分） 即$\frac{1}{2}\times5\times5\sqrt{2}\times\frac{\sqrt{6}+\sqrt{2}}{4}=\frac{1}{2}\times5\times AE\times\frac{\sqrt{3}}{2}+\frac{1}{2}\times AE\times5\sqrt{2}\times\frac{\sqrt{2}}{2}$， 解得$AE = 5\sqrt{3}-5$. （15 分） 解法二：因为$\frac{AE}{EC}=\frac{S_{\triangle ABD}}{S_{\triangle BCD}}=\frac{\frac{1}{2}AB\cdot AD\cdot\sin\angle BAD}{\frac{1}{2}BC\cdot CD\cdot\sin\angle BCD}=\frac{\sqrt{3}}{3}$（提示：利用面积的比值得到线段的比值），即$EC=\sqrt{3}AE$， （13 分） 又因为$AC = 10$，所以$AE + EC = 10$， 则$AE+\sqrt{3}AE = 10$， 解得$AE = 5\sqrt{3}-5$. （15 分）

17. (15分)
甲公司现有资金200万元，考虑一项投资计划，假定影响投资收益的唯一因素是投资期间的经济形势，若投资期间经济形势好，投资有25%的收益率，若投资期间经济形势不好，投资有10%的损益率；如果不执行该投资计划，损失为1万元.现有两个方案，方案一：执行投资计划；方案二：聘请投资咨询公司乙分析投资期间的经济形势，聘请费用为5 000元，若投资咨询公司乙预测投资期间经济形势好，则执行投资计划；若投资咨询公司乙预测投资期间经济形势不好，则不执行该计划.根据以往的资料表明，投资咨询公司乙预测不一定正确，投资期间经济形势好，咨询公司乙预测经济形势好的概率是0.8；投资期间经济形势不好，咨询公司乙预测经济形势不好的概率是0.7.假设根据权威资料可以确定，投资期间经济形势好的概率是40%，经济形势不好的概率是60%.
(Ⅰ)求投资咨询公司乙预测投资期间经济形势好的概率；
(Ⅱ)根据获得利润的期望值的大小，甲公司应该执行哪个方案？说明理由.

答案：  全概率公式 + 条件概率公式 + 离散型随机变量的分布列及期望 【思维导图】(Ⅰ)设事件$B_{1}$，$B_{2}$，$A\to P(B_{1})$，$P(B_{2})\to P(A)$. (Ⅱ)分别列出方案一、二获得利润值的分布列$\to$求出其对应的期望$\to$比较期望大小$\to$得解. 解：(Ⅰ)记投资期间经济形势好为事件$B_{1}$，投资期间经济形势不好为事件$B_{2}$，投资咨询公司乙预测投资期间经济形势好为事件$A$， 则$P(B_{1})=0.4$，$P(B_{2})=0.6$， （4 分） 因此$P(A)=P(B_{1}A + B_{2}A)=P(B_{1})P(A|B_{1})+P(B_{2})P(A|B_{2})=0.4\times0.8+0.6\times0.3 = 0.5$. （7 分） (Ⅱ)若采取方案一，则该公司获得的利润值$X$万元的分布列是 | $X$ | $50$ | $-20$ | | $P$ | $0.4$ | $0.6$ | (提醒：负值代表着亏损) 则$E(X)=50\times0.4-20\times0.6 = 8$（万元）； （9 分） 若采取方案二：设该公司获得的利润值为$Y$万元，有以下情况， 投资期间经济形势好，咨询公司乙预测经济形势为好，$Y = 49.5$，其发生的概率为$P(B_{1}A)=0.4\times0.8 = 0.32$； 投资期间经济形势好，咨询公司乙预测经济形势为不好，$Y=-1.5$，其发生的概率为$P(B_{1}\overline{A})=0.4\times0.2 = 0.08$； 投资期间经济形势不好，咨询公司乙预测经济形势为好，$Y=-20.5$，其发生的概率为$P(B_{2}A)=0.6\times0.3 = 0.18$； 投资期间经济形势不好，咨询公司乙预测经济形势为不好，$Y=-1.5$，其发生的概率为$P(B_{2}\overline{A})=0.6\times0.7 = 0.42$， （13 分） 所以随机变量$Y$的分布列为 | $Y$ | $-20.5$ | $-1.5$ | $49.5$ | | $P$ | $0.18$ | $0.5$ | $0.32$ | (题眼) 则$E(Y)=-20.5\times0.18-1.5\times0.5 + 49.5\times0.32=-3.69-0.75 + 15.84 = 11.4$（万元）. （14 分） 因为$E(X)\lt E(Y)$，所以甲公司应该执行方案二. （15 分）