第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
11. 英国著名物理学家牛顿用“作切线”的方法求函数零点。已知二次函数$f(x)$有两个不相等的实根$b$,$c$,其中$c > b$。在函数$f(x)$图象上横坐标为$x_{1}$的点处作曲线$y = f(x)$的切线,切线与$x$轴交点的横坐标为$x_{2}$;用$x_{2}$代替$x_{1}$,重复以上的过程得到$x_{3}$;一直下去,得到数列$\{ x_{n}\}$。记$a_{n}=\ln\frac{x_{n}-b}{x_{n}-c}$,且$a_{1}=1$,$x_{n}>c$,下列说法正确的是 ( )
A. $x_{1}=\frac{ec - b}{e - 1}$(其中$\ln e = 1$)
B. 数列$\{ a_{n}\}$是递减数列
C. $a_{6}=\frac{1}{32}$
D. 数列$\{ a_{n}+\frac{1}{a_{n}}\}$的前$n$项和$S_{n}=2^{n}-2^{1 - n}+1$
A. $x_{1}=\frac{ec - b}{e - 1}$(其中$\ln e = 1$)
B. 数列$\{ a_{n}\}$是递减数列
C. $a_{6}=\frac{1}{32}$
D. 数列$\{ a_{n}+\frac{1}{a_{n}}\}$的前$n$项和$S_{n}=2^{n}-2^{1 - n}+1$
答案:
ACD
12. 将1到10这10个正整数平均分成甲、乙两组,每组5个正整数,且甲组的中位数比乙组的中位数小1,则不同的平分方法共有_______种。
答案:
56
13. 如图,圆$A:(x + 2)^{2}+y^{2}=1$,圆$B:(x - 2)^{2}+y^{2}=4$,直线$3x + 4y + t = 0$上存在点$P$,过点$P$向圆$A$引两条切线$PC$和$PD$,切点是$C$和$D$,再过点$P$向圆$B$引两条切线$PE$和$PF$,切点是$E$和$F$,若$\angle CPD=\angle EPF$,则实数$t$的取值范围为_______。
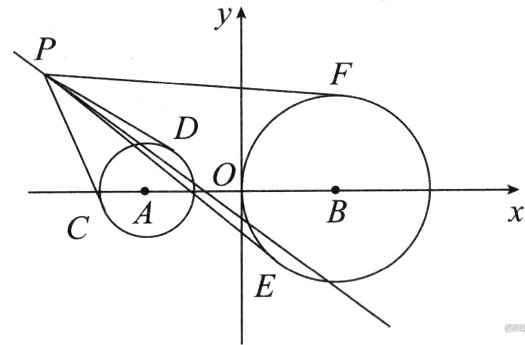

答案:
$[-15,25]$
14. 某同学在学习和探索三角形相关知识时,发现了一个有趣的性质:将锐角三角形三条边所对的外接圆的三条圆弧(劣弧)沿着三角形的边进行翻折,则三条圆弧交于该三角形内部一点,且此交点为该三角形的垂心(即三角形三条高线的交点)。如图,已知锐角$\triangle ABC$外接圆的半径为2,且三条圆弧沿$\triangle ABC$三边翻折后交于点$P$。若$AB = 3$,则$\sin\angle PAC =$_______;若$AC:AB:BC = 6:5:4$,则$PA + PB + PC$的值为_______。
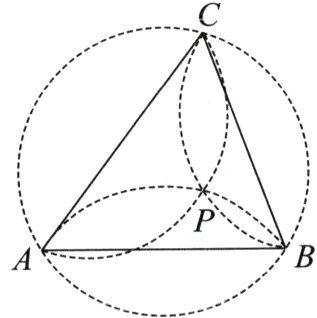

答案:
$\frac{3}{4}$;$\frac{15\sqrt{7}}{2}$
四、解答题:本题共5小题,共77分。解答应写出文字说明、证明过程或演算步骤。
15. (13分)
已知椭圆$C_{1}$,抛物线$C_{2}$的焦点均在$x$轴上,$C_{1}$的中心和$C_{2}$的顶点均为坐标原点$O$,从$C_{1}$,$C_{2}$上分别取两个点,将其坐标记录于表中:
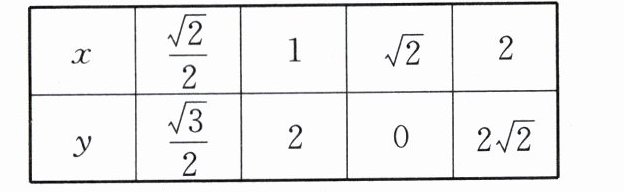
(Ⅰ)求$C_{1}$和$C_{2}$的标准方程;
(Ⅱ)若$C_{1}$和$C_{2}$交于不同的两点$A$,$B$,求$\overrightarrow{OA}\cdot\overrightarrow{OB}$的值。
15. (13分)
已知椭圆$C_{1}$,抛物线$C_{2}$的焦点均在$x$轴上,$C_{1}$的中心和$C_{2}$的顶点均为坐标原点$O$,从$C_{1}$,$C_{2}$上分别取两个点,将其坐标记录于表中:

(Ⅰ)求$C_{1}$和$C_{2}$的标准方程;
(Ⅱ)若$C_{1}$和$C_{2}$交于不同的两点$A$,$B$,求$\overrightarrow{OA}\cdot\overrightarrow{OB}$的值。
答案:
椭圆的标准方程 + 抛物线的标准方程 + 平面向量的数量积 解:(Ⅰ)设抛物线 \(C_{2}\) 的标准方程为 \(y^{2}=2px(p\gt0)\),则 \(2p=\frac{y^{2}}{x}\). 因为 \(\frac{2^{2}}{1}=\frac{(2\sqrt{2})^{2}}{2}=4\),所以点 \((1,2)\),\((2,2\sqrt{2})\) 在抛物线 \(C_{2}\) 上,且 \(2p = 4\),解得 \(p = 2\),所以抛物线 \(C_{2}\) 的标准方程为 \(y^{2}=4x\). 设椭圆 \(C_{1}\) 的标准方程为 \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a\gt b\gt0)\),将点 \((\frac{\sqrt{2}}{2},\frac{\sqrt{3}}{2})\),\((\sqrt{2},0)\) 的坐标分别代入椭圆 \(C_{1}\) 的标准方程 \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1(a\gt b\gt0)\) 中,得 \(\begin{cases}\frac{1}{2a^{2}}+\frac{3}{4b^{2}}=1\\\frac{2}{a^{2}}=1\end{cases}\),解得 \(a^{2}=2\),\(b^{2}=1\),则椭圆 \(C_{1}\) 的标准方程为 \(\frac{x^{2}}{2}+y^{2}=1\). (Ⅱ)根据对称性,可设 \(A\),\(B\) 两点坐标分别为 \((x_{0},y_{0})\),\((x_{0},-y_{0})\),联立 \(\begin{cases}y^{2}=4x\\x^{2}+2y^{2}=2\end{cases}\),消 \(y\) 得 \(x^{2}+8x - 2 = 0\),解得 \(x_{1}=-4 - 3\sqrt{2}\),\(x_{2}=-4 + 3\sqrt{2}\). 因为 \(x=\frac{y^{2}}{4}\geqslant0\),所以 \(x_{0}=3\sqrt{2}-4\),所以 \(\overrightarrow{OA}\cdot\overrightarrow{OB}=x_{0}^{2}-y_{0}^{2}=x_{0}^{2}-4x_{0}=(3\sqrt{2}-4)^{2}-4(3\sqrt{2}-4)=50 - 36\sqrt{2}\).
查看更多完整答案,请扫码查看


