第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
10. 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,$P$为线段$BD_{1}$上的动点,直线$m$为平面$A_{1}DP$与平面$B_{1}CP$的交线,则( )
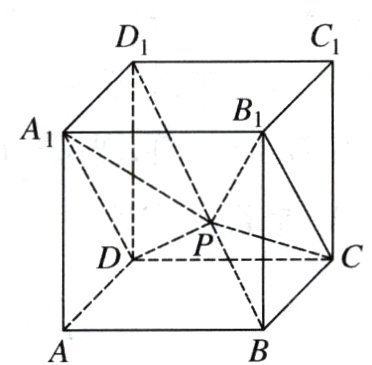
A. 存在点$P$,使得$BB_{1} //$平面$A_{1}DP$
B. 存在点$P$,使得$B_{1}P \perp$平面$A_{1}DP$
C. 当点$P$不是$BD_{1}$的中点时,都有$m //$平面$A_{1}B_{1}CD$
D. 当点$P$不是$BD_{1}$的中点时,都有$m \perp$平面$ABD_{1}$

A. 存在点$P$,使得$BB_{1} //$平面$A_{1}DP$
B. 存在点$P$,使得$B_{1}P \perp$平面$A_{1}DP$
C. 当点$P$不是$BD_{1}$的中点时,都有$m //$平面$A_{1}B_{1}CD$
D. 当点$P$不是$BD_{1}$的中点时,都有$m \perp$平面$ABD_{1}$
答案:
ACD
11. 设等比数列$\{ a_{n} \}$的公比为$q$,前$n$项积为$T_{n}$,下列说法正确的是( )
A. 若$T_{8} = T_{12}$,则$a_{10}a_{11} = 1$
B. 若$T_{8} = T_{12}$,则$T_{20} = 1$
C. 若$a_{1} = 1024$,且$T_{10}$为数列$\{ T_{n} \}$的唯一最大项,则$(\frac{1}{2})^{\frac{1}{9}} \lt q \lt \frac{1}{2}$
D. 若$a_{1} \gt 0$,且$T_{10} \gt T_{11} \gt T_{9}$,则使得$T_{n} \gt 1$成立的$n$的最大值为20
A. 若$T_{8} = T_{12}$,则$a_{10}a_{11} = 1$
B. 若$T_{8} = T_{12}$,则$T_{20} = 1$
C. 若$a_{1} = 1024$,且$T_{10}$为数列$\{ T_{n} \}$的唯一最大项,则$(\frac{1}{2})^{\frac{1}{9}} \lt q \lt \frac{1}{2}$
D. 若$a_{1} \gt 0$,且$T_{10} \gt T_{11} \gt T_{9}$,则使得$T_{n} \gt 1$成立的$n$的最大值为20
答案:
BCD
12. 已知函数$f(x)$是定义在$\mathbf{R}$上的增函数,且$f(2) = 1$,则不等式$f(x) \gt 5 - 2x$的解集为_______.
答案:
$(2,+\infty)$
13. 已知$A(4,1)$,$B(2,2)$,$C(0,3)$,若在圆$x^{2} + y^{2} = r^{2}(r \gt 0)$上存在点$P$满足$|PA|^{2} + |PB|^{2} + |PC|^{2} = 13$,则实数$r$的取值范围是_______.
答案:
$[2\sqrt{2} - 1,2\sqrt{2} + 1]$
14. 已知正四棱锥$P - ABCD$的顶点均在球$O$的表面上. 若正四棱锥的体积为1,则球$O$体积的最小值为_______.
答案:
$\frac{27}{16}\pi$
15. (13分)
如图1,在矩形$ABCD$中,$AB = 2$,$BC = 2\sqrt{3}$,将$\triangle ABD$沿矩形的对角线$BD$进行翻折,得到如图2所示的三棱锥$A - BCD$.
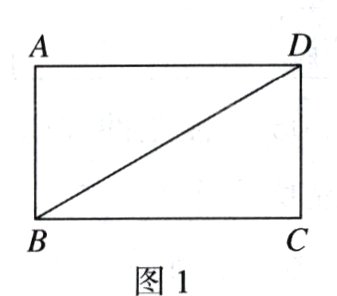
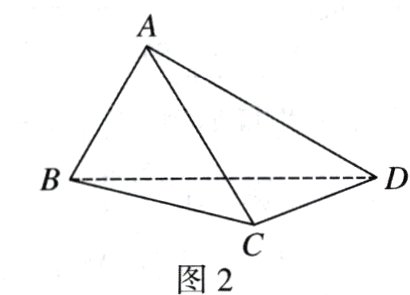
(Ⅰ)当$AB \perp CD$时,求$AC$的长;
(Ⅱ)当平面$ABD \perp$平面$BCD$时,求平面$ABC$和平面$ACD$的夹角的余弦值.
如图1,在矩形$ABCD$中,$AB = 2$,$BC = 2\sqrt{3}$,将$\triangle ABD$沿矩形的对角线$BD$进行翻折,得到如图2所示的三棱锥$A - BCD$.


(Ⅰ)当$AB \perp CD$时,求$AC$的长;
(Ⅱ)当平面$ABD \perp$平面$BCD$时,求平面$ABC$和平面$ACD$的夹角的余弦值.
答案:
线面垂直的判定定理与性质定理 + 平面与平面夹角的余弦值 解:(Ⅰ)由$AB\perp CD$,$BC\perp CD$,且$AB\cap BC = B$,$AB$,$BC\subset$平面$ABC$, 可得$CD\perp$平面$ABC$(题眼)(方法:线面垂直的判定定理)。 又$AC\subset$平面$ABC$,所以$AC\perp CD$。 在矩形$ABCD$中,$AD = BC = 2\sqrt{3}$,$CD = AB = 2$。 在$Rt\triangle ACD$中,根据勾股定理, 得$AC = \sqrt{AD^{2} - CD^{2}} = \sqrt{(2\sqrt{3})^{2} - 2^{2}} = 2\sqrt{2}$。 (5 分) (Ⅱ)如图,过点$A$作$AO\perp BD$于点$O$,过点$C$作$CE\perp BD$于点$E$,易知$AO = \sqrt{3}$,$OB = 1$,$OD = 3$,$CE = \sqrt{3}$,$BE = 3$,$OE = 2$, 由平面$ABD\perp$平面$BCD$,平面$ABD\cap$平面$BCD = BD$,$AO\subset$平面$ABD$,可得$AO\perp$平面$BCD$。 如图,以$O$为坐标原点,在平面$BCD$中,过点$O$作$BD$的垂线为$x$轴,$OD$,$OA$所在直线分别为$y$,$z$轴,建立空间直角坐标系, 则$A(0,0,\sqrt{3})$,$B(0,-1,0)$,$C(\sqrt{3},2,0)$,$D(0,3,0)$, 则$\overrightarrow{AB} = (0,-1,-\sqrt{3})$,$\overrightarrow{BC} = (\sqrt{3},3,0)$,$\overrightarrow{CD} = (-\sqrt{3},1,0)$,$\overrightarrow{AD} = (0,3,-\sqrt{3})$。 设平面$ABC$的法向量$\boldsymbol{m} = (x_{1},y_{1},z_{1})$, 则$\begin{cases}\boldsymbol{m}\cdot\overrightarrow{AB} = -y_{1} - \sqrt{3}z_{1} = 0\\\boldsymbol{m}\cdot\overrightarrow{BC} = \sqrt{3}x_{1} + 3y_{1} = 0\end{cases}$, 令$z_{1} = 1$,得$y_{1} = -\sqrt{3}$,$x_{1} = 3$,所以$\boldsymbol{m} = (3,-\sqrt{3},1)$; 设平面$ACD$的法向量$\boldsymbol{n} = (x_{2},y_{2},z_{2})$, 则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{CD} = -\sqrt{3}x_{2} + y_{2} = 0\\\boldsymbol{n}\cdot\overrightarrow{AD} = 3y_{2} - \sqrt{3}z_{2} = 0\end{cases}$, 令$x_{2} = 1$,得$y_{2} = \sqrt{3}$,$z_{2} = 3$, 所以$\boldsymbol{n} = (1,\sqrt{3},3)$, 从而$|\cos\langle\boldsymbol{m},\boldsymbol{n}\rangle| = \frac{|\boldsymbol{m}\cdot\boldsymbol{n}|}{|\boldsymbol{m}||\boldsymbol{n}|} = \frac{3}{\sqrt{13}\times\sqrt{13}} = \frac{3}{13}$(方法:空间向量的夹角公式), 即平面$ABC$和平面$ACD$的夹角的余弦值为$\frac{3}{13}$。 (13 分)
查看更多完整答案,请扫码查看


