第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
16. (15 分)
据新华社北京 2 月 26 日报道,中国航天全年预计实施 100 次左右发射任务,有望创造新的纪录,我国首个商业航天发射场将迎来首次发射任务,多个卫星星座将加速组网建设;中国航天科技集团有限公司计划安排近 70 次宇航发射任务,发射 290 余个航天器,实施一系列重大工程任务. 由于航天行业拥有广阔的发展前景,有越来越多的公司开始从事航天研究,某航天公司研发了一种火箭推进器,为测试其性能,对推进器飞行距离与损坏零件数进行了统计,数据如下:
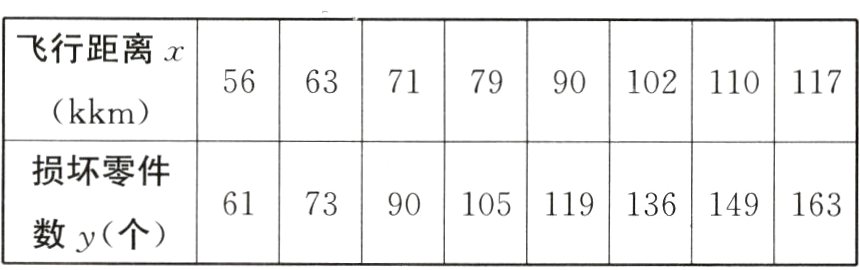
参考数据:$\overline{x}=86$,$\overline{y}=112$,$\sum_{i = 1}^{8}x_{i}y_{i}=82743$,$\sum_{i = 1}^{8}x_{i}^{2}=62680$
(Ⅰ)建立 y 关于 x 的回归模型$\hat{y}=\hat{b}x+\hat{a}$,根据所给数据及回归模型,求 y 关于 x 的回归方程($\hat{b}$精确到 0.1,$\hat{a}$精确到 1);
(Ⅱ)该公司进行了第二项测试,从所有同型号推进器中随机抽取 100 台进行等距离飞行测试,对其中 60 台进行飞行前保养,测试结束后,有 20 台报废,其中保养过的推进器占比 30%,请根据统计数据完成 2×2 列联表,并根据小概率值$\alpha = 0.01$的独立性检验,能否认为推进器是否报废与保养有关?

附:回归方程$\hat{y}=\hat{b}x+\hat{a}$中斜率和截距的最小二乘估计公式分别为$\hat{b}=\frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}$,$\hat{a}=\overline{y}-\hat{b}\overline{x}$,$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,$n = a + b + c + d$;

据新华社北京 2 月 26 日报道,中国航天全年预计实施 100 次左右发射任务,有望创造新的纪录,我国首个商业航天发射场将迎来首次发射任务,多个卫星星座将加速组网建设;中国航天科技集团有限公司计划安排近 70 次宇航发射任务,发射 290 余个航天器,实施一系列重大工程任务. 由于航天行业拥有广阔的发展前景,有越来越多的公司开始从事航天研究,某航天公司研发了一种火箭推进器,为测试其性能,对推进器飞行距离与损坏零件数进行了统计,数据如下:

参考数据:$\overline{x}=86$,$\overline{y}=112$,$\sum_{i = 1}^{8}x_{i}y_{i}=82743$,$\sum_{i = 1}^{8}x_{i}^{2}=62680$
(Ⅰ)建立 y 关于 x 的回归模型$\hat{y}=\hat{b}x+\hat{a}$,根据所给数据及回归模型,求 y 关于 x 的回归方程($\hat{b}$精确到 0.1,$\hat{a}$精确到 1);
(Ⅱ)该公司进行了第二项测试,从所有同型号推进器中随机抽取 100 台进行等距离飞行测试,对其中 60 台进行飞行前保养,测试结束后,有 20 台报废,其中保养过的推进器占比 30%,请根据统计数据完成 2×2 列联表,并根据小概率值$\alpha = 0.01$的独立性检验,能否认为推进器是否报废与保养有关?

附:回归方程$\hat{y}=\hat{b}x+\hat{a}$中斜率和截距的最小二乘估计公式分别为$\hat{b}=\frac{\sum_{i = 1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i = 1}^{n}(x_{i}-\overline{x})^{2}}$,$\hat{a}=\overline{y}-\hat{b}\overline{x}$,$\chi^{2}=\frac{n(ad - bc)^{2}}{(a + b)(c + d)(a + c)(b + d)}$,$n = a + b + c + d$;

答案:
回归直线方程 + 独立性检验 解:(Ⅰ)由题意得 \(\hat{b}=\frac{\sum_{i = 1}^{8}(x_i-\overline{x})(y_i-\overline{y})}{\sum_{i = 1}^{8}(x_i-\overline{x})^2}\) \(=\frac{\sum_{i = 1}^{8}x_iy_i-8\overline{x}\overline{y}}{\sum_{i = 1}^{8}x_i^2-8\overline{x}^2}\)(提示:利用最小二乘估计公式求 \(\hat{b}\)) \(=\frac{82743-8\times86\times112}{62680-8\times86^2}\approx1.6\), \(\hat{a}=\overline{y}-\hat{b}\overline{x}\approx - 26\), 故 \(y\) 关于 \(x\) 的线性回归方程为 \(\hat{y}=1.6x - 26\). (7 分) (Ⅱ)设零假设为 \(H_0\):是否报废与是否保养无关. 由题意,报废推进器中保养过的共有 \(20\times30\% = 6\)(台),未保养的推进器共有 \(20 - 6 = 14\)(台). 补充 \(2\times2\) 列联表如下: | | 保养 | 未保养 | 合计 | |----|----|----|----| | 报废 | 6 | 14 | 20 | | 未报废 | 54 | 26 | 80 | | 合计 | 60 | 40 | 100 | (11 分) 则 \(\chi^2=\frac{100\times(6\times26 - 14\times54)^2}{20\times60\times40\times80}=9.375\gt6.635\)(题眼), (14 分) 根据小概率值 \(\alpha = 0.01\) 的独立性检验,推断 \(H_0\) 不成立,即认为是否报废与是否保养有关,此推断错误的概率不大于 \(0.01\). (15 分)
17. (15 分)
在三棱锥$P - ABC$中,$PB\perp$平面 ABC,$AB = BC = BP = 2$,点 E 在平面 ABC 内,且满足平面$PAE\perp$平面 PBE,$BA\perp BC$.
(Ⅰ)当$\angle ABE\in[\frac{\pi}{8},\frac{\pi}{3}]$时,求点 E 的轨迹长度;
(Ⅱ)当二面角$E - PA - B$的余弦值为$\frac{\sqrt{3}}{3}$时,求三棱锥$E - PCB$的体积.
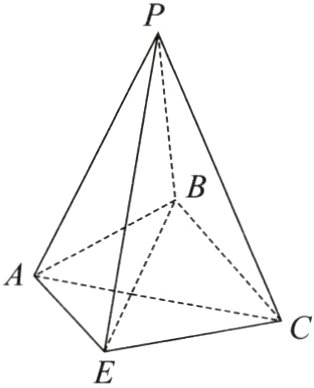
在三棱锥$P - ABC$中,$PB\perp$平面 ABC,$AB = BC = BP = 2$,点 E 在平面 ABC 内,且满足平面$PAE\perp$平面 PBE,$BA\perp BC$.
(Ⅰ)当$\angle ABE\in[\frac{\pi}{8},\frac{\pi}{3}]$时,求点 E 的轨迹长度;
(Ⅱ)当二面角$E - PA - B$的余弦值为$\frac{\sqrt{3}}{3}$时,求三棱锥$E - PCB$的体积.

答案:
空间中直线与平面间的位置关系 + 二面角的余弦值 + 三棱锥的体积公式 + 动点的轨迹长度 【思维导图】(Ⅰ)作 \(BH\perp PE\) 交 \(PE\) 于点 \(H\xrightarrow{面面垂直的性质定理}BH\perp\) 平面 \(PAE\to BH\perp AE\xrightarrow{线面垂直的性质定理}PB\perp AE\to AE\perp\) 平面 \(PBE\to AE\perp BE\xrightarrow{建系,设 E(x,y,0)}\overrightarrow{AE}\cdot\overrightarrow{BE}=0\) 点 \(E\) 的轨迹方程 \(\xrightarrow{\angle ABE 的范围}\angle ANE\) 的范围→点 \(E\) 的轨迹长度. (Ⅱ)平面 \(PAE\) 的一个法向量,\(\overrightarrow{BC}\xrightarrow{空间向量夹角公式}\) 点 \(E\) 的坐标 \(\xrightarrow{三棱锥的体积公式}得解. 解:(Ⅰ)作 \(BH\perp PE\) 交 \(PE\) 于点 \(H\), 因为平面 \(PAE\perp\) 平面 \(PBE\),且平面 \(PAE\cap\) 平面 \(PBE = PE\), 所以 \(BH\perp\) 平面 \(PAE\). 又 \(AE\subset\) 平面 \(PAE\),所以 \(BH\perp AE\). 因为 \(PB\perp\) 平面 \(ABC\),且 \(AE\subset\) 平面 \(ABC\), 所以 \(PB\perp AE\). 因为 \(BH\perp AE,PB\perp AE,PB,BH\subset\) 平面 \(PBE,PB\cap BH = B\), 所以 \(AE\perp\) 平面 \(PBE\), 又 \(BE\subset\) 平面 \(PBE\),所以 \(AE\perp BE\)(题眼). 以 \(B\) 为坐标原点,分别以直线 \(BA,BC,BP\) 为 \(x\) 轴、\(y\) 轴、\(z\) 轴建立空间直角坐标系,如图 1, 则 \(B(0,0,0),P(0,0,2),C(0,2,0),A(2,0,0)\). 设 \(E(x,y,0)\),则 \(\overrightarrow{AE}=(x - 2,y,0),\overrightarrow{BE}=(x,y,0)\), 因为 \(AE\perp BE\),所以 \(\overrightarrow{AE}\cdot\overrightarrow{BE}=0\), 所以 \((x - 2)\cdot x + y\cdot y = 0\),即 \((x - 1)^2 + y^2 = 1\)(提示:将垂直关系转化为向量的数量积为 0,进而求动点的轨迹方程). (5 分) 设 \(AB\) 的中点为 \(N\),则 \(N(1,0)\), 如图 2, 又 \(\angle ABE\in[\frac{\pi}{8},\frac{\pi}{3}]\), 所以 \(\angle ANE\in[\frac{\pi}{4},\frac{2\pi}{3}]\)(提示:圆心角与圆周角的关系), 因此 \(E\) 的轨迹为圆弧 \(QE\),其长度为 \((\frac{2\pi}{3}-\frac{\pi}{4})\times1=\frac{5\pi}{12}\). (7 分) (Ⅱ)由(Ⅰ)知,\(\overrightarrow{PA}=(2,0,-2),\overrightarrow{AE}=(x - 2,y,0)\), 设平面 \(PAE\) 的法向量为 \(\boldsymbol{n}=(a,b,c)\), 则 \(\begin{cases}\boldsymbol{n}\cdot\overrightarrow{PA}=0\\\boldsymbol{n}\cdot\overrightarrow{AE}=0\end{cases}\),即 \(\begin{cases}2a - 2c = 0\\a(x - 2)+by = 0\end{cases}\), 令 \(a = y\),则 \(b = 2 - x,c = y,\boldsymbol{n}=(y,2 - x,y)\). (10 分) \(\overrightarrow{BC}=(0,2,0)\) 为平面 \(PAB\) 的一个法向量. 设二面角 \(E - PA - B\) 的平面角为 \(\theta\), \(\cos\theta=\frac{|\boldsymbol{n}\cdot\overrightarrow{BC}|}{|\boldsymbol{n}||\overrightarrow{BC}|}=\frac{|x - 2|}{\sqrt{(x - 2)^2 + 2y^2}}\), 因为 \((x - 1)^2 + y^2 = 1\), 所以 \(\cos\theta=\frac{|x - 2|}{\sqrt{4 - x^2}}=\frac{\sqrt{3}}{3}\)(题眼), 解得 \(x = 2,y = 0\)(舍去)或 \(x = 1,y = \pm1\), 则 \(E(1,1,0)\) 或 \(E(1,-1,0)\), (13 分) 所以 \(V_{E - PCB}=\frac{1}{3}\times\frac{1}{2}\times2\times2\times1=\frac{2}{3}\). (15 分)
查看更多完整答案,请扫码查看


