《2025年高考模拟试题汇编高中数学》

1. 已知集合$M = \{ x|x \lt 1 \} $，$N = \{ x|x^{2} \lt 1 \} $，则( )
A. $M = N$
B. $M \subseteq N$
C. $N \subseteq M$
D. $M \cap N = \varnothing$

答案： C

2. 复数$z = \frac{\mathrm{i}}{2 - \mathrm{i}}$在复平面内对应的点位于( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限

答案： B

3. 若抛物线$y^{2} = ax$的焦点坐标为$(1,0)$，则实数$a$的值为( )
A. $-2$
B. $2$
C. $-4$
D. $4$

答案： D

4. 如图是函数$y = A\sin(\omega x + \varphi )$的部分图象，则该函数的解析式可以是( )

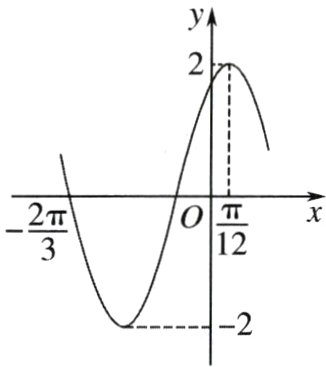
A. $y = 2\sin(\frac{1}{2}x + \frac{\pi}{3})$
B. $y = 2\sin(\frac{1}{2}x - \frac{\pi}{3})$
C. $y = 2\sin(2x + \frac{\pi}{3})$
D. $y = 2\sin(2x - \frac{\pi}{3})$

答案： C

5. 已知甲盒中有3个红球和2个黄球，乙盒中有2个红球和1个黄球，且这些球的大小质地完全相同. 现从甲盒中随机抽取1个球放入乙盒中，搅拌均匀后，再从乙盒中随机抽取1个球，此球恰为红球的概率是( )
A. $\frac{3}{8}$
B. $\frac{9}{20}$
C. $\frac{5}{8}$
D. $\frac{13}{20}$

答案： D

6. 若$\tan2\alpha + 4\tan(\alpha + \frac{\pi}{4}) = 0$，则$\sin2\alpha =$( )
A. $-\frac{4}{5}$
B. $-\frac{2}{5}$
C. $\frac{2}{5}$
D. $\frac{4}{5}$

答案： A

7. 已知直线$y = a$与函数$f(x) = \mathrm{e}^{x}$，$g(x) = \ln x$的图象分别相交于$A$，$B$两点. 设$k_{1}$为曲线$y = f(x)$在点$A$处切线的斜率，$k_{2}$为曲线$y = g(x)$在点$B$处切线的斜率，则$k_{1}k_{2}$的最大值为( )
A. $\frac{1}{\mathrm{e}}$
B. 1
C. $\mathrm{e}$
D. $\mathrm{e}^{2}$

答案： A

8. 在平面四边形$ABCD$中，$E$，$F$分别为$AD$，$BC$的中点. 若$AB = 2$，$CD = 3$，且$\overrightarrow{EF} \cdot \overrightarrow{AB} = 4$，则$|\overrightarrow{EF}| =$( )
A. $\frac{\sqrt{17}}{2}$
B. $\frac{\sqrt{21}}{2}$
C. $\frac{\sqrt{42}}{2}$
D. $\sqrt{5}$

答案： B

9. 某彗星的运行轨道是以太阳为一个焦点的椭圆.测得轨道的近日点(距离太阳最近的点)与太阳中心的距离为$d_{1}$，远日点(距离太阳最远的点)与太阳中心的距离为$d_{2}$，并且近日点、远日点及太阳中心在同一条直线上，则( )
A. 轨道的焦距为$d_{2} + d_{1}$
B. 轨道的离心率为$\frac{d_{2} - d_{1}}{d_{2} + d_{1}}$
C. 轨道的短轴长为$2\sqrt{d_{1}d_{2}}$
D. 当$\frac{d_{1}}{d_{2}}$越大时，轨道越扁

答案： BC