《2025年高考模拟试题汇编高中数学》

11. 已知函数$f(x)=\cos x+\vert\sin\frac{x}{2}\vert$，则 ( )
A. $f(x)$在区间$(0,\frac{\pi}{6})$上单调递增
B. $f(x)$的图象关于直线$x = \pi$对称
C. $f(x)$的值域为$[0,\frac{9}{8}]$
D. 关于$x$的方程$f(x)=a$在区间$[0,2\pi]$上有实数根，则所有根之和组成的集合为$\{\pi,2\pi,4\pi\}$

答案：
ABD

12. 已知集合$A = \{ -1,0,1\}$，$B = \{ y\mid y = 2x,x\in A\}$，则$A\cup B$的所有元素之和为_______.

答案： 0

13. 已知$O$为坐标原点，$F$为椭圆$C:\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$($a＞b＞0$)的右焦点，点$A$，$B$在$C$上，$AB$的中点为$F$，$OA\perp OB$，则$C$的离心率为_______.

答案： $\frac{\sqrt{6}}{3}$

14. 已知球$O$的表面积为$12\pi$，正四面体$ABCD$的顶点$B$，$C$，$D$均在球$O$的表面上，球心$O$为$\triangle BCD$的外心，棱$AB$与球面交于点$P$. 若$A\in$平面$\alpha_{1}$，$B\in$平面$\alpha_{2}$，$C\in$平面$\alpha_{3}$，$D\in$平面$\alpha_{4}$，$\alpha_{i}//\alpha_{i + 1}(i = 1,2,3)$且$\alpha_{i}$与$\alpha_{i + 1}(i = 1,2,3)$之间的距离为同一定值，棱$AC$，$AD$分别与$\alpha_{2}$交于点$Q$，$R$，则$\triangle PQR$的周长为_______.

答案：
$3\sqrt{3}$

15.(13分)
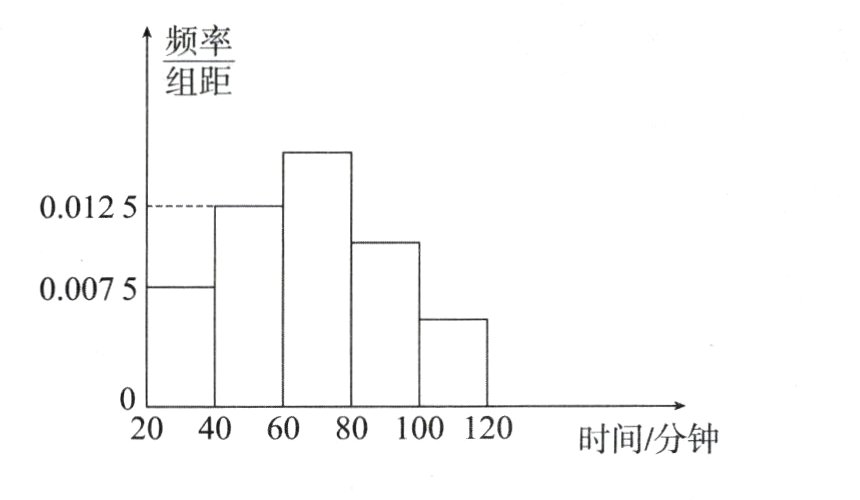
为促进全民阅读，建设书香校园，某校在寒假面向全体学生发出“读书好、读好书、好读书”的号召，并开展阅读活动. 开学后，学校统计了高一年级共1000名学生的假期日均阅读时间(单位：分钟)，得到了如图所示的频率分布直方图，若前两个小矩形的高度分别为0.0075，0.0125，后三个小矩形的高度比为3∶2∶1.
(Ⅰ)根据频率分布直方图，估计高一年级1000名学生假期日均阅读时间的平均值(同一组中的数据用该组区间的中点值为代表)；
(Ⅱ)开学后，学校从高一日均阅读时间不低于60分钟的学生中，按照分层随机抽样的方式，抽取6名学生作为代表分两周进行国旗下演讲，假设第一周演讲的3名学生日均阅读时间处于$[80,100)$的人数记为$\xi$，求随机变量$\xi$的分布列与数学期望.

答案： 平均数 + 离散型随机变量的分布列与数学期望 解：(Ⅰ)由题知，各组频率分别为\(0.15,0.25,0.3,0.2,0.1\) (题眼)， 日均阅读时间的平均值为\(30\times0.15 + 50\times0.25+70\times0.3 + 90\times0.2+110\times0.1 = 67\). (Ⅱ)由题意，在\([60,80)\)，\([80,100)\)，\([100,120]\)三组分别抽取\(3,2,1\)人， \(\xi\)的可能取值为\(0,1,2\) (题眼)， 则\(P(\xi = 0)=\frac{C_{3}^{0}C_{2}^{0}}{C_{6}^{2}}=\frac{1}{5}\)， \(P(\xi = 1)=\frac{C_{3}^{1}C_{2}^{1}}{C_{6}^{2}}=\frac{3}{5}\)， \(P(\xi = 2)=\frac{C_{3}^{2}C_{2}^{0}}{C_{6}^{2}}=\frac{1}{5}\)， 则\(\xi\)的分布列为 | \(\xi\) | \(0\) | \(1\) | \(2\) | | ---- | ---- | ---- | ---- | | \(P\) | \(\frac{1}{5}\) | \(\frac{3}{5}\) | \(\frac{1}{5}\) | \(E(\xi)=0\times\frac{1}{5}+1\times\frac{3}{5}+2\times\frac{1}{5}=1\) (提示：数学期望计算公式). 

16.(15分)
已知函数$f(x)=\frac{1}{2}x^{2}-ax+\ln x$.
(Ⅰ)若$a = 1$，曲线$y = f(x)$在点$(x_{0},f(x_{0}))$处的切线斜率为1，求该切线的方程；
(Ⅱ)讨论$f(x)$的单调性.

答案：  导数的几何意义 + 利用导数研究函数的单调性 解：(Ⅰ)当\(a = 1\)时，\(f^{\prime}(x)=\frac{x^{2}-x + 1}{x}\)， 则\(f^{\prime}(x_{0}) = 1\) (题眼)， 解得\(x_{0}=1\). 因为\(f
(1)=-\frac{1}{2}\)， 所以切线方程为\(x - y-\frac{3}{2}=0\). (Ⅱ)已知\(f(x)\)的定义域为\((0,+\infty)\)，\(f^{\prime}(x)=\frac{x^{2}-ax + 1}{x}\) (题眼)， 当\(a\leqslant0\)时，得\(f^{\prime}(x)\gt0\)恒成立，\(f(x)\)在\((0,+\infty)\)上单调递增； 当\(a\gt0\)时，令\(g(x)=x^{2}-ax + 1\)，\(\Delta=a^{2}-4\)， (ⅰ)当\(\Delta\leqslant0\)，即\(0\lt a\leqslant2\)时， \(f^{\prime}(x)\geqslant0\)恒成立，\(f(x)\)在\((0,+\infty)\)上单调递增； (ⅱ)当\(\Delta\gt0\)，即\(a\gt2\)时， \(f^{\prime}(x)=\frac{(x-\frac{a-\sqrt{a^{2}-4}}{2})(x-\frac{a+\sqrt{a^{2}-4}}{2})}{x}\)， 由\(f^{\prime}(x)\gt0\)，得\(0\lt x\lt\frac{a-\sqrt{a^{2}-4}}{2}\)或\(x\gt\frac{a+\sqrt{a^{2}-4}}{2}\)， 由\(f^{\prime}(x)\lt0\)，得\(\frac{a-\sqrt{a^{2}-4}}{2}\lt x\lt\frac{a+\sqrt{a^{2}-4}}{2}\)， 所以\(f(x)\)在\((0,\frac{a-\sqrt{a^{2}-4}}{2})\)，\((\frac{a+\sqrt{a^{2}-4}}{2},+\infty)\)上单调递增， 在\((\frac{a-\sqrt{a^{2}-4}}{2},\frac{a+\sqrt{a^{2}-4}}{2})\)上单调递减. 综上，当\(a\leqslant2\)时，\(f(x)\)在\((0,+\infty)\)上单调递增； 当\(a\gt2\)时，\(f(x)\)在\((0,\frac{a-\sqrt{a^{2}-4}}{2})\)，\((\frac{a+\sqrt{a^{2}-4}}{2},+\infty)\)上单调递增，\(f(x)\)在\((\frac{a-\sqrt{a^{2}-4}}{2},\frac{a+\sqrt{a^{2}-4}}{2})\)上单调递减. 

17.(15分)
如图，在三棱柱$ABC - A_{1}B_{1}C_{1}$中，$AA_{1}$与$BB_{1}$的距离为$\sqrt{3}$，$AB = AC = A_{1}B = 2$，$A_{1}C = BC = 2\sqrt{2}$.
(Ⅰ)证明：平面$A_{1}ABB_{1}\perp$平面$ABC$；
(Ⅱ)若点$N$在棱$A_{1}C_{1}$上，求直线$AN$与平面$A_{1}B_{1}C$所成角的正弦值的最大值.

答案：
空间中线面间的位置关系 + 线面角的正弦值 + 空间向量的应用 解：(Ⅰ)证明：取棱$A_{1}A$的中点$D$，连接$BD$， 因为$AB = A_{1}B$，所以$BD\perp AA_{1}$. 因为三棱柱$ABC - A_{1}B_{1}C_{1}$， 所以$AA_{1}// BB_{1}$， 所以$BD\perp BB_{1}$，所以$BD=\sqrt{3}$. 因为$AB = 2$，所以$AD = 1$，所以$AA_{1}=2$. 因为$AC = 2$，$A_{1}C = 2\sqrt{2}$， 所以$AC^{2}+AA_{1}^{2}=A_{1}C^{2}$，所以$AC\perp AA_{1}$ (题眼)， 同理$AC\perp AB$. 因为$AA_{1}\cap AB = A$，且$AA_{1},AB\subset$平面$A_{1}ABB_{1}$， 所以$AC\perp$平面$A_{1}ABB_{1}$ (提示：线面垂直的判定定理). 又因为$AC\subset$平面$ABC$， 所以平面$A_{1}ABB_{1}\perp$平面$ABC$ (提示：面面垂直的判定定理). (Ⅱ)取$AB$的中点$O$，连接$A_{1}O$， 取$BC$的中点$P$，连接$OP$，则$OP// AC$， 由(Ⅰ)知$AC\perp$平面$A_{1}ABB_{1}$， 所以$OP\perp$平面$A_{1}ABB_{1}$ (题眼). 因为$A_{1}O\subset$平面$A_{1}ABB_{1}$，$AB\subset$平面$A_{1}ABB_{1}$， 所以$OP\perp A_{1}O$，$OP\perp AB$. 因为$AB = A_{1}A = A_{1}B$，则$A_{1}O\perp AB$. 以$O$为坐标原点，$OP,OB,OA_{1}$所在的直线分别为$x$轴、$y$轴、$z$轴，建立如图所示的空间直角坐标系$O - xyz$， 则$A(0,-1,0)$，$A_{1}(0,0,\sqrt{3})$，$B_{1}(0,2,\sqrt{3})$，$C(2,-1,0)$， 设点$N(a,0,\sqrt{3})(0\leqslant a\leqslant2)$， 则$\overrightarrow{A_{1}B_{1}}=(0,2,0)$，$\overrightarrow{A_{1}C}=(2,-1,-\sqrt{3})$，$\overrightarrow{AN}=(a,1,\sqrt{3})$， 设平面$A_{1}B_{1}C$的法向量为$\boldsymbol{n}=(x,y,z)$， 则$\begin{cases}\boldsymbol{n}\cdot\overrightarrow{A_{1}B_{1}} = 0\\\boldsymbol{n}\cdot\overrightarrow{A_{1}C}=0\end{cases}$，即$\begin{cases}2y = 0\\2x - y-\sqrt{3}z = 0\end{cases}$， 取$x=\sqrt{3}$，则$y = 0$，$z = 2$， 则$\boldsymbol{n}=(\sqrt{3},0,2)$. 设直线$AN$与平面$A_{1}B_{1}C$所成角为$\theta$， 则$\sin\theta=\vert\cos\langle\boldsymbol{n},\overrightarrow{AN}\rangle\vert=\frac{\vert\boldsymbol{n}\cdot\overrightarrow{AN}\vert}{\vert\boldsymbol{n}\vert\cdot\vert\overrightarrow{AN}\vert}=\frac{\sqrt{3}(a + 2)}{\sqrt{7}\cdot\sqrt{a^{2}+4}}=\frac{\sqrt{3}}{\sqrt{7}}\cdot\sqrt{\frac{(a + 2)^{2}}{a^{2}+4}}=\frac{\sqrt{3}}{\sqrt{7}}\sqrt{\frac{a^{2}+4a + 4}{a^{2}+4}}$ (提示：空间向量的夹角公式)， 若$a = 0$，则$\sin\theta=\frac{\sqrt{21}}{7}$； 若$a\neq0$，则$\sin\theta=\frac{\sqrt{3}}{\sqrt{7}}\cdot\sqrt{1+\frac{4}{a+\frac{4}{a}}}\leqslant\frac{\sqrt{3}}{\sqrt{7}}\times\sqrt{1+\frac{4}{4}}=\frac{\sqrt{42}}{7}$ (提示：基本不等式的应用)， 当且仅当$a=\frac{4}{a}$，即$a = 2$时，等号成立， 所以直线$AN$与平面$A_{1}B_{1}C$所成角的正弦值的最大值为$\frac{\sqrt{42}}{7}$.

18.(17分)
已知$O$为坐标原点，$W$为$\odot O:x^{2}+y^{2}=4$和$\odot M$的公共点，$\overrightarrow{OM}\cdot\overrightarrow{OW}=0$，$\odot M$与直线$x + 2 = 0$相切，记动点$M$的轨迹为$C$.
(Ⅰ)求$C$的方程；
(Ⅱ)若$n＞m＞0$，直线$l_{1}:x - y - m = 0$与$C$交于点$A$，$B$，直线$l_{2}:x - y - n = 0$与$C$交于点$A'$，$B'$，点$A$，$A'$在第一象限，记直线$AA'$与$BB'$的交点为$G$，直线$AB'$与$BA'$的交点为$H$，线段$AB$的中点为$E$.
(ⅰ)证明：$G$，$E$，$H$三点共线；
(ⅱ)若$(m + 1)^{2}+n = 7$，过点$H$作$l_{1}$的平行线，分别交线段$AA'$，$BB'$于点$T$，$T'$，求四边形$GTET'$面积的最大值.

答案： 轨迹方程 + 直线与抛物线的位置关系 + 基本不等式的应用 【思维导图】(Ⅰ)已知条件\(\xrightarrow{设M(x,y),\odot M与直线x + 2 = 0的切点为N}\vert MN\vert^{2}=\vert MW\vert^{2}=\vert OM\vert^{2}+\vert OW\vert^{2}\to得解\). (Ⅱ)(ⅰ)已知条件\(\to\)设\(\overrightarrow{GA}=\lambda\overrightarrow{GA^{\prime}},\overrightarrow{GB}=\lambda\overrightarrow{GB^{\prime}}(\lambda\neq0)\)，记\(A^{\prime}B^{\prime}\)的中点为\(F\to G,E,F\)三点共线\(\xrightarrow{同理}H,E,F\)三点共线\(\to\)得证. (ⅱ)已知条件\(\xrightarrow{设A(x_{1},y_{1}),B(x_{2},y_{2}),A^{\prime}(x_{3},y_{3}),B^{\prime}(x_{4},y_{4})}联立l_{1}与C的方程\to y_{1}+y_{2},y_{1}y_{2}\xrightarrow{同理}y_{3}+y_{4},y_{3}y_{4},y_{F}\xrightarrow{平行线间距离相等}S_{四边形GTET^{\prime}}=S_{四边形GAHB}\to设G(x_{G},2),H(x_{H},2)\to直线AA^{\prime}的方程\to x_{G},x_{H}\to GH\xrightarrow{基本不等式}得解\). 解：(Ⅰ)设\(M(x,y)\)，\(\odot M\)与直线\(x + 2 = 0\)的切点为\(N\)， 则\(\vert MN\vert^{2}=\vert MW\vert^{2}=\vert OM\vert^{2}+\vert OW\vert^{2}\) (题眼)， 所以\(\vert x + 2\vert^{2}=x^{2}+y^{2}+4\)， 化简得\(y^{2}=4x\)，所以\(C\)的方程为\(y^{2}=4x\). (Ⅱ)(ⅰ)证明：因为\(l_{1}\parallel l_{2}\)， 不妨设\(\overrightarrow{GA}=\lambda\overrightarrow{GA^{\prime}},\overrightarrow{GB}=\lambda\overrightarrow{GB^{\prime}}(\lambda\neq0)\)， 记\(A^{\prime}B^{\prime}\)的中点为\(F\)， 因为\(\overrightarrow{GE}=\frac{1}{2}(\overrightarrow{GA}+\overrightarrow{GB})=\frac{\lambda}{2}(\overrightarrow{GA^{\prime}}+\overrightarrow{GB^{\prime}})=\lambda\overrightarrow{GF}(\lambda\neq0)\) (题眼)， 所以\(G,E,F\)三点共线，同理\(H,E,F\)三点共线， 所以\(G,E,H\)三点共线. (ⅱ)设\(A(x_{1},y_{1})\)，\(B(x_{2},y_{2})\)，\(A^{\prime}(x_{3},y_{3})\)，\(B^{\prime}(x_{4},y_{4})\)， 联立\(\begin{cases}x - y - m = 0\\y^{2}=4x\end{cases}\)得\(y^{2}-4y - 4m = 0\) (题眼)， \(\Delta=16 + 16m\gt0\)， 所以\(y_{1}+y_{2}=4\)，\(y_{1}y_{2}=-4m\)， 所以\(y_{E}=\frac{y_{1}+y_{2}}{2}=2\)， 同理\(y_{3}+y_{4}=4\)，\(y_{3}y_{4}=-4n\)，\(y_{F}=2\)， 则\(G,E,H,F\)四点均在定直线\(y = 2\)上. 因为\(TT^{\prime}\parallel l_{1}\)，所以\(\triangle EAT\)与\(\triangle EAH\)的面积相等，\(\triangle EBT^{\prime}\)与\(\triangle EBH\)的面积相等(提示：平行线间的距离相等)， 所以四边形\(GTET^{\prime}\)的面积等于四边形\(GAHB\)的面积. 设\(G(x_{G},2)\)，\(H(x_{H},2)\)， 直线\(AA^{\prime}:y - y_{1}=\frac{y_{1}-y_{3}}{x_{1}-x_{3}}(x - x_{1})\)， 即\(y - y_{1}=\frac{y_{1}-y_{3}}{\frac{y_{1}^{2}}{4}-\frac{y_{3}^{2}}{4}}(x - \frac{y_{1}^{2}}{4})\)， 整理得直线\(AA^{\prime}:y=\frac{4x + y_{1}y_{3}}{y_{1}+y_{3}}\)， 又因为\(y_{G}=2\)，所以\(x_{G}=\frac{2(y_{1}+y_{3})-y_{1}y_{3}}{4}\)， 同理，直线\(BA^{\prime}:y=\frac{4x + y_{2}y_{3}}{y_{2}+y_{3}}\)，因为\(y_{H}=2\)， 所以\(x_{H}=\frac{2(y_{2}+y_{3})-y_{2}y_{3}}{4}\)， 所以\(\vert GH\vert=\vert x_{G}-x_{H}\vert=\vert\frac{(y_{1}-y_{2})(2 - y_{3})}{4}\vert=\vert\frac{(y_{1}-y_{2})(\frac{y_{3}+y_{4}}{2}-y_{3})}{4}\vert=\frac{\vert(y_{1}-y_{2})(y_{3}-y_{4})\vert}{8}\)， 所以四边形\(GAHB\)的面积 \(S=\frac{1}{2}\vert GH\vert\cdot\vert y_{1}-y_{2}\vert=\frac{(y_{1}-y_{2})^{2}\cdot\vert y_{3}-y_{4}\vert}{16}=\frac{[(y_{1}+y_{2})^{2}-4y_{1}y_{2}]\cdot\sqrt{(y_{3}+y_{4})^{2}-4y_{3}y_{4}}}{16}=\frac{(16 + 16m)\cdot\sqrt{16 + 16n}}{16}=4\sqrt{(1 + m)^{2}(1 + n)}\leqslant4[\frac{(1 + m)^{2}+1 + n}{2}]=16\) (提示：基本不等式的应用)， 当且仅当\((1 + m)^{2}=1 + n\)，即\(\begin{cases}m = 1\\n = 3\end{cases}\)时取等号， 所以四边形\(GTET^{\prime}\)面积的最大值为\(16\). 

19.(17分)
记集合$S = \{\{ a_{n}\}\mid$无穷数列$\{ a_{n}\}$中存在有限项不为零，$n\in\mathbf{N}^{*}\}$，对任意$\{ a_{n}\}\in S$，设变换$f(\{ a_{n}\}) = a_{1}+a_{2}x+\cdots+a_{n}x^{n - 1}+\cdots$，$x\in\mathbf{R}$.
定义运算$\otimes$：若$\{ a_{n}\}$，$\{ b_{n}\}\in S$，则$\{ a_{n}\}\otimes\{ b_{n}\}\in S$，$f(\{ a_{n}\}\otimes\{ b_{n}\}) = f(\{ a_{n}\})\cdot f(\{ b_{n}\})$.
(Ⅰ)若$\{ a_{n}\}\otimes\{ b_{n}\}=\{ m_{n}\}$，用$a_{1}$，$a_{2}$，$a_{3}$，$a_{4}$，$b_{1}$，$b_{2}$，$b_{3}$，$b_{4}$表示$m_{4}$；
(Ⅱ)证明：$(\{ a_{n}\}\otimes\{ b_{n}\})\otimes\{ c_{n}\}=\{ a_{n}\}\otimes(\{ b_{n}\}\otimes\{ c_{n}\})$；
(Ⅲ)若$a_{n}=\begin{cases}\frac{(n + 1)^{2}+1}{n(n + 1)},1\leqslant n\leqslant100,\\0,n＞100,\end{cases}$
$b_{n}=\begin{cases}(\frac{1}{2})^{203 - n},1\leqslant n\leqslant500,\\0,n＞500,\end{cases}$ $\{ d_{n}\}=\{ a_{n}\}\otimes\{ b_{n}\}$，
证明：$d_{200}＜\frac{1}{2}$.

答案： 新定义 + 裂项相消法求数列的和 【思维导图】(Ⅰ)已知条件\(\xrightarrow{新定义}得解\). (Ⅱ)已知条件\(\to f(\{ a_{n}\})\cdot f(\{ b_{n}\})\cdot f(\{ c_{n}\})=f((\{ a_{n}\otimes\{ b_{n}\})\otimes\{ c_{n}\})=f(\{ a_{n}\otimes(\{ b_{n}\otimes\{ c_{n}\}))\to得证\). (Ⅲ)已知条件\(\to\{ d_{n}\}\to\{ a_{n}\otimes\{ b_{n}\}=\{ d_{n}\}\to d_{200}\xrightarrow{裂项相消法}得证\). 解：(Ⅰ)因为\(m_{4}x^{3}=(a_{1}b_{4}+a_{2}b_{3}+a_{3}b_{2}+a_{4}b_{1})x^{3}\) (题眼)， 所以\(m_{4}=a_{1}b_{4}+a_{2}b_{3}+a_{3}b_{2}+a_{4}b_{1}\). (Ⅱ)证明：因为\(f(\{ a_{n}\otimes\{ b_{n}\})=f(\{ a_{n}\})\cdot f(\{ b_{n}\})\)， 所以\(f(\{ a_{n}\})\cdot f(\{ b_{n}\})\cdot f(\{ c_{n}\})=f(\{ a_{n}\otimes\{ b_{n}\})\cdot f(\{ c_{n}\})=f((\{ a_{n}\otimes\{ b_{n}\})\otimes\{ c_{n}\})\). 又因为\(f(\{ a_{n}\})\cdot f(\{ b_{n}\})\cdot f(\{ c_{n}\})=f(\{ a_{n}\})\cdot[f(\{ b_{n}\})\cdot f(\{ c_{n}\})]=f(\{ a_{n}\})\cdot f(\{ b_{n}\otimes\{ c_{n}\})=f(\{ a_{n}\otimes(\{ b_{n}\otimes\{ c_{n}\}))\)， 所以\(f((\{ a_{n}\otimes\{ b_{n}\})\otimes f\{ c_{n}\})=f(\{ a_{n}\otimes(\{ b_{n}\otimes f\{ c_{n}\}))\)， 所以\((\{ a_{n}\otimes\{ b_{n}\})\otimes\{ c_{n}\}=\{ a_{n}\otimes(\{ b_{n}\otimes\{ c_{n}\})\). (Ⅲ)证明：对于\(\{ a_{n}\},\{ b_{n}\}\in S\)， 因为\((a_{1}+a_{2}x+\cdots+a_{n}x^{n - 1}+\cdots)(b_{1}+b_{2}x+\cdots+b_{n}x^{n - 1}+\cdots)=d_{1}+d_{2}x+\cdots+d_{n}x^{n - 1}+\cdots\)， 所以\(d_{n}x^{n - 1}=a_{1}(b_{n}x^{n - 1})+a_{2}x(b_{n - 1}x^{n - 2})+\cdots+a_{k}x^{k - 1}\cdot(b_{n + 1 - k}x^{n - k})+\cdots+a_{n - 1}x^{n - 2}(b_{2}x)+a_{n}x^{n - 1}b_{1}\)， 所以\(d_{n}=a_{1}b_{n}+a_{2}b_{n - 1}+\cdots+a_{k}b_{n + 1 - k}+\cdots+a_{n - 1}b_{2}+a_{n}b_{1}\)， 所以\(\{ a_{n}\otimes\{ b_{n}\}=\{ d_{n}\}=\{\sum_{k = 1}^{n}a_{k}b_{n + 1 - k}\}\) (题眼)， \(d_{200}=\sum_{k = 1}^{200}a_{k}b_{201 - k}=\sum_{k = 1}^{100}a_{k}b_{201 - k}+\sum_{k = 101}^{200}a_{k}b_{201 - k}=\sum_{k = 1}^{100}a_{k}b_{201 - k}=\sum_{k = 1}^{100}\frac{(k + 1)^{2}+1}{k(k + 1)2^{k + 2}}\)， 所以\(d_{200}=\sum_{k = 1}^{100}\frac{1}{2^{k + 2}}(1+\frac{2}{k}-\frac{1}{k + 1})=\sum_{k = 1}^{100}\frac{1}{2^{k + 2}}+\sum_{k = 1}^{100}[\frac{1}{k\cdot2^{k + 1}}-\frac{1}{(k + 1)\cdot2^{k + 2}}]\) (提示：裂项相消法求数列的和) \(=\frac{1}{2}-\frac{102}{101\times2^{102}}\lt\frac{1}{2}\). (解析人：杜 伟)