《2025年高考模拟试题汇编高中数学》

10. 已知偶函数$f(x)$的定义域为$\mathbf{R},f\left(\frac{1}{2}x + 1\right)$为奇函数，且$f(x)$在$[0,1]$上单调递增，则下列结论正确的是( )
A. $f\left(-\frac{3}{2}\right)＜0$
B. $f\left(\frac{4}{3}\right)＞0$
C. $f(3)＜0$
D. $f\left(\frac{2024}{3}\right)＞0$

答案：
10.BD　函数的对称性和周期性+函数的奇偶性
　　　　　　　　　　　　　　　　　　　　　　1
[思维导图]已知条件函数的对称性＞函数f(x)的周期为4:作出函数f(x)在[−2,2]上的大致图象得解.　±因为偶函数f(x)的定义域为R,f($\frac{1}{2}$x+1)为奇函数,所f(−$\frac{1}{2}$x+1)=−f($\frac{1}{2}$x+1),即有f(−x+1)=−f(x+1),则函数f(x)的图象关于点(1,0)对称，即f(一x)=
　−f(x+2),令x=−1,得f
(1)=0,又f(−x)=f(x),所以f(x)=一f(x+2),所以函数f(x)的周期为4,作出函数f(x)在[−2,2]上的大致图象，如图所示，对于A，f(−$\frac{3}{2}${＞0,故A错误;对于B,f($\frac{4}{3}${＞0,故B正确;对
于C,f
(3)=f(−1)=0,故C错误;对于D,f($\frac{2024}{3}$)=
　　　f(($\frac{2028}{3}$−$\frac{4}{3}$)=f(169×4−$\frac{4}{3}$)=f(−$\frac{4}{3}$)＞0,故D正
　　　确，故选BD.

11. 已知正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的各个顶点都在表面积为$3\pi$的球面上，$P$为该球面上的任意一点，则下列结论正确的是( )
A. 有无数个点$P$，使得$AP//$平面$BDC_{1}$
B. 有无数个点$P$，使得$AP\perp$平面$BDC_{1}$
C. 若点$P\in$平面$BCC_{1}B_{1}$，则四棱锥$P - ABCD$的体积的最大值为$\frac{\sqrt{2}+1}{6}$
D. 若点$P\in$平面$BCC_{1}B_{1}$，则$AP + PC_{1}$的最大值为$\sqrt{6}$

答案：
11.ACD正方体的外接球+面面平行的判定定理及性质定理+
　　　棱锥的体积公式+三角恒等变换+基本不等式的应用
　　　I;[思维导图]面面平行的判定定理及性质定理＞判断选项A;;　
　　　　线面垂直的性质定理判断选项B;
　　　　球棱的锥截的面体圆积的公性式质判断选项C;
　　　;　　利用点P的坐标表示AP十PC1
　　　1　　　　　　　　　　　　　　　AP+PC1=$\sqrt{2+x}$+|
　　　:三角恒等变换，令$\frac{\sqrt{2}}{2}$(sinθ+cosθ)=x
A1　$\sqrt{1−x}$基本不等式判断选项D.　　　　　　　　　　　1
　　　令正方体ABCD−AlBClD的外接球半径为r,根据题意，
　　　得4πr²=3π,解得r=$\frac{\sqrt{3}}{2}$,则BD=$\sqrt{3}$,故AB=1,AD1=
　　　$\sqrt{2}$.对于A,如图1,连接AB,AD,B1D1,BD,DC,BG,由
D是该正方体的对角面，得四边形ABCD是D//BC,又BCC平面BDC,ADC平面
D//平面BDC,同理AB//平面BDC，又
A,AB,ADC平面ABD,所以平面ABD//
　　　平面BDC1，记平面ABlD1截球面所得的截面小圆为圆M，
　　　则圆M上任意一点P(除点A外),均有AP/平面BDC1，故
A选项正确;对于B,过点A与平面BDC垂直的直线AP仅
　　　有一条，故这样的点P至多有一个(提示:根据线面垂直的性
　　　质定理判断),故B选项错误;对于C,记平面BCClB1截球面
　　　所得的截面小圆为圆R,则圆R的半径为$\frac{\sqrt{2}}{2}$,圆R上的点到
底面ABCD的距离的最大值为$\frac{\sqrt{2}+1}{2}$(提醒:注意圆上的点到直线的距离的最大值为圆心到直线的距离加半径)，所以四棱锥P一ABCD的体积的最大值为$\frac{1}{3}$×1×$\frac{\sqrt{2}+1}{2}$=$\frac{\sqrt{2}+1}{6}$,故
C选项正确;对于D,易知AB⊥平面BCCB1，在平面
BCCB内建立平面直角坐标系，如图2,令点P与x轴所成角为θ(0≤θ＜2π)，则P($\frac{2}{2}$cosθ,$\frac{\sqrt{2}}{2}$sine)，又
B(−$\frac{1}{2}$,−$\frac{1}{2}${,C,($\frac{1}{2}$,$\frac{1}{2}${,所以AP=　$\sqrt{AB²+BP²}$=
　　$\sqrt{1²+(\frac{√2}{2}+)+(\frac{√2}{2}sin+)}$$\sqrt{2+(s)}$
　PC1=　　　　　　　　　　　　　=/$\sqrt{\frac{√2}{2}(sinθ+cosθ)}$1　　　　　　,令$\frac{\sqrt{2}}{2}$(sinθ+cos0)=x,则AP+PC=$\sqrt{2+x}$+$\sqrt{1−x}$=
　　$\sqrt{(√2+x+\sqrt{1−x})²}$$\sqrt{2[(√2+x)²+(\sqrt{1−x}歼}$=
　$\sqrt{6}$(提示:利用$\frac{a+b}{2}$≤$\sqrt{a²+b²}$求解，利用基本不等式求取值范围时应注意需满足条件“一正，二定，三相等”，对不满足条件的可通过“变形”来转换，常见的变形技巧有:拆项、并项、1代换),当且仅当x=一$\frac{1}{2}$时取等号，此时$\frac{\sqrt{2}}{2}$(sinθ+cosθ)=
　$\frac{1}{2}$,即sin(0+$\frac{π}{4}$)=−$\frac{1}{2}$,所以当点PE平面BCCB时，
AP+PC的最大值为　$\sqrt{6}$,故D选项正确，故选ACD.

12. 随机变量$X\sim N(\mu,\sigma^{2})$，若$P(X\geqslant70)=P(X\leqslant90)$且$P(72\leqslant X\leqslant80)=0.3$，则随机变量$X$的第80百分位数是______。

答案： 12.88　百分位数+正态分布的性质　因为随机变量X~N(μ,σ²),P(X≥70)=P(X≤90),所以μ=80,故P(80≤X≤88)=
　P(72≤X≤80)=0.3,则P(X≤88)=0.5+P(80≤X≤88)=
　0.8(题眼),所以随机变量X的第80百分位数是88.

13. 已知函数$f(x)=\sin(\omega x+\varphi)(\omega＞0)$在区间$\left(\frac{\pi}{6},\frac{7\pi}{12}\right)$上单调，且满足$f\left(\frac{\pi}{6}\right)=-1,f\left(\frac{7\pi}{4}\right)=0$，则$\omega =$______。

答案： 13.$\frac{6}{7}$　正弦型函数的图象与性质　因为函数∮(x)
　(m＞0)在区间($\frac{π}{6}$,$\frac{7π}{12}$)上单调,所以$\frac{7π}{12}$$\frac{π}{6}$$\frac{1}{2}$
　$\frac{12}{5}$，又f($\frac{π}{6}$)=−1,f($\frac{3π}{4}${=0,所以$\frac{π}{6}$w+=2kπ+$\frac{3π}{2}$,k∈Z,
　　　　　　　　　　　解得一$\frac{7π}{12}$纠=(2k1−k2)π+$\frac{3π}{2}$,$\frac{3π}{4}$w+=k2π,　　　k2∈Z,
　{
　k1,k2∈Z,令2k1−k2=−2,解得幼=%

14. 已知直线$l$与椭圆$C:\frac{x^{2}}{3}+\frac{y^{2}}{2}=1$在第一象限交于$P,Q$两点，$l$与$x$轴、$y$轴分别交于$M,N$两点，且满足$\frac{|PM|}{|QM|}+\frac{|QM|}{|PM|}=\frac{|PN|}{|QN|}+\frac{|QN|}{|PN|}$，则$l$的斜率为______。

答案：
14.−$\frac{\sqrt{6}}{3}$　直线与椭圆的位置关系+直线的斜率+对勾函数的性质
[思维导图]设点P在点Q的左侧，R是PQ的中点，
　　　P(x1,y1),Q(x2,y2)→点R的坐标→直线l的斜率k，
　　　直线OR的斜率koR　将点P，Q的坐点标差代法入椭圆的方程
　　　　　　　　$\frac{|PM|}{|QM|}$$\frac{IQN|}{PN}$　　　　　　　　检验
　　　kOR.k=−$\frac{2}{3}$$\frac{|QMITPNE(1,+00)}{对勾函数的性质}$k=−$\frac{\sqrt{6}}{3}$位得解.
　　　如图所示，不妨设点P在点Q的左侧，R是PQ的中点，P(x1,y),Q(x22,y2),则R($\frac{x+x2}{2}$,$\frac{y+y2}{2}$),,可得直线l 的斜率k=xy¹−−yx²2,直线OR的斜率koR=$\frac{y+y2}{x+x2}$.因为P(x1,y1),Q(x2,y2)在椭圆C:$\frac{x²}{3}$+辽2=1上,则$\frac{x²}{3}$+$\frac{y²}{2}$=1,
　　　　　　　两式相减得$\frac{x²−x2}{3}$+$\frac{y²−y²}{2}$=0,整理得$\frac{x2}{3}$+$\frac{y2}{2}$=1,
　　{
　　　$\frac{y²−y²}{x²−x²}$=−$\frac{2}{3}$,即koR.k=−$\frac{2}{3}$.易知$\frac{|PM|}{QM}$,$\frac{|QN|}{PN}$∈(1,+oa),又f(x)=x+$\frac{1}{x}$在(1,十∞)上单调递增,所以由$\frac{|PM|}{|QM|}$+$\frac{|QM|}{|PM|}$=$\frac{|PN}{|QN}$+$\frac{|QN|}{|PN}$,得$\frac{|PM|}{QM}$=$\frac{|QN|}{PN}$,即$\frac{|PQ|+|QM|}{|QM|}$=
　　　$\frac{|PQ|+|PN|}{|PN}$,整理得|QM|=|PN|,所以R为MN的中点，所以|OR|=|RM|,所以koR=−k,结合koR.k=一$\frac{2}{3}$
　　　可得k²=$\frac{2}{3}$,且k＜0,解得k=一$\frac{\sqrt{6}}{3}$,检验k=−$\frac{\sqrt{6}}{3}$符合题意,所以直线/的斜率为.

四、解答题:本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤。
15. (13分)
已知$0 ＜ a ＜ 1$，函数$f(x)=\frac{a\text{e}^{x - a}}{x}(x\neq0)$。
(Ⅰ)求$f(x)$的单调区间。
(Ⅱ)讨论方程$f(x)=a$的根的个数。

答案： 函数的单调性+函数的零点
　　　　　　　得f'(x)=$\frac{ae−a(x−1)}{x²}$.　　　　　　　(3分)
　　　因为a＞0,er−"＞0,　　　　　　　　　　　　　　(4分)
　　　所以当x＜1且x≠0时,f'(x)＜0;当x＞1时,f'(x)＞0(提示:可利用导数的正负判断函数的单调区间，注意恒大于0的条件)，　　　　　　　　　　　　　　　　　　　　(6分)
　　　所
　　　递增.　　　　　　　　　　　　　　　　　　　　(7分)
(III)当x＜0时,因为a＞0,e²−＞0,
　所以f(x)=$\frac{aer−a}{x}$＜0＜a,　　　　　　　　　　　　(8分)
　所以f(x)=a在(一∞o,0)上有0个根;　　　　　　　(9分)
　当x＞0时,由(I)得,f(x)的最小值为f
(1)=ae¹−a.
　　　　　　　　　　　　　　　　　　　　(10分)
　因为0＜a＜1,所以0＜1−a＜1,
　所以elα＞1(易错:根据函数值判断f(x)的图象与直线y=
　a的交点个数，注意x的范围)，
　所以f
(1)=ae¹−α＞a,　　　　　　　　　　　　　(11分)
　所以f(x)=a在(0,十oo)上有0个根.　　　　　　(12分)
　综上所述，方程f(x)=a有0个根.　　　　　　　　(13分)

16. (15分)
如图，已知圆柱$OO_{1}$的轴截面$ABCD$是边长为2的正方形，$P$是圆$O_{1}$上异于点$C,D$的任意一点。
(Ⅰ)若点$D$到平面$ACP$的距离为$\frac{2\sqrt{3}}{3}$，证明:$O_{1}P\perp CD$。
(Ⅱ)求$OC$与平面$ACP$所成角的正弦值的取值范围。

答案：
16.点到平面的距离+线面垂直的判定定理与性质定理+空间向量的应用+线面角的正弦值
　

天利因为CD是圆O，的直径，所以CP⊥DP.　　　　　(2分)
　因为AD是圆柱侧面的母线，所以AD⊥平面CDP，
　又CPC平面CDP,所以AD⊥CP.　　　　　　　　(3分)
　因为AD,DPC平面ADP,AD∩DP=D,
　所以CP⊥平面ADP.　　　　　　　　　　　　　　(4分)
　因为DHC平面ADP,所以DH⊥CP(方法:借助线面垂直的性质定理判断线线垂直)，
　又DH⊥AP,AP,CPC平面ACP,AP∩CP=P,
所以DH⊥平面ACP，　　　　　　　　　　　　　(5分)
　　所以点D到平面ACP的距离为DH,即DH=$\frac{2\sqrt{3}}{3}$(题眼).
　　设DP=a(a＞0),则AP=$\sqrt{a²+4}$
　　由AD.DP=AP.DH,得2.a=　$\sqrt{a²+4}$.$\frac{2\sqrt{3}}{3}$,
　　解得a=$\sqrt{2}$.　　　　　　　　　　　　　　　　　　(6分)
　　因为CD=2,所以PC=DP=　$\sqrt{2}$.
　　因为O1是CD的中点，所以OP⊥CD.　　　　　　(7分)
　　(III)解法一:如图2,在平面PCD内,过点O1作OlE⊥OC 交圆O，于点E，连接001，
　　　　　　　　
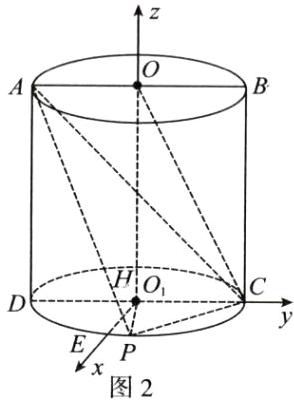
　　因为OO⊥平面PCD，
　　所以OE,O1C,OO两两相互垂直，以O1为坐标原点，分
　　别以OE,OC,OO所在直线为x,y,N轴建立空间直角坐
　　标系，　　　　　　　　　　　　　　　　　　　　(8分)
　　则O(0,0,2),C(0,1,0),A(0,−1,2).
　　设点P(m,n,0),因为点P在圆O上，
　　所以m²+n²=1,n∈(−1,1),
　　则OC=(0,1,−2),AC=(0,2,−2),CP=(m,,n−1,0).
　　　　　　　　　　　　　　　　　　　　　(9分)
　　设平面ACP的法向量n=(x,y,N),
　　则{nn..ACCP==0o,,艮卩{m2yx−+2(xn=−01,)y=0,
　　　　y=z,
　　解得
　　　　y=−　　　,
　　　　{
　　　　　　$\frac{m}{(n−1)}$
　　取x=n−1,得n=(n−1,−m,−m).　　　　　　(10分)
　　设OC与平面ACP所成角为θ，
＞1=||忒OC|.|nnl||=$\frac{|m|}{\sqrt{5}.√2m²+(n−1)²}$
　　　　　　　　　　　　　1　　　　(提示:线面角的正
　　$\sqrt{5}$.　$\sqrt{2+\frac{(n−1)}{m²}}$　$\sqrt{5}$.　$\sqrt{\frac{(n−1)}{1−n²}}$2+
　　弦值恰为直线方向向量与平面法向量所成角的余弦值的绝
　　对值).　　　　　　　　　　　　　　　　　　　　(12分)
　　因为$\frac{(n−1)²}{1−n²}$=$\frac{(n−1)(n−1)}{(1−n)(1+n)}$=−$\frac{n−1}{1+n}$=−1+$\frac{2}{1+n}$,
　　且n∈(−1,1)(方法:利用分离常量法将分子分母都有变量
　　的函数转换为分子无变量的函数，便于求其值域)，
所以−1+$\frac{2}{1+n}$∈(0,+∞。),
　所以$\sqrt{\frac{(n−1)}{1−n²}}$2+　　　　=　2+(−1+$\frac{2}{1+n}$)∈($\sqrt{2}$,+8),
　　　　　　　　　　　　　　　　　　　(14分)
　所以sinθ=　　　　1　　　　∈(0,$\frac{\sqrt{10}}{10}${,
　　　　　$\sqrt{5}$.　$\sqrt{\frac{(n−1)}{1−n²}}$2+
　所以OC与平面ACP所成角的正弦值的取值范围是$\frac{0}{10}$.　　　　　　　　　　　　　　　　　　(15分)
　解法二:由(I)知,点D到平面ACP的距离为DH.
　连接OD交AC于点F,如图3.
　　　　　　　
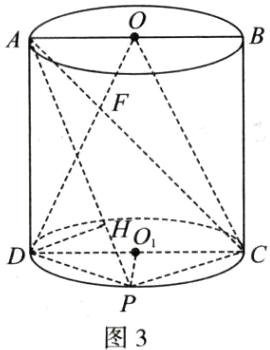
　因为OA//CD,且OA=$\frac{1}{2}$CD,
　所以OF=$\frac{1}{2}$DF,
　所以点O到平面ACP的距离为$\frac{1}{2}$DH.　　　　　　(9分)
　在Rt△ADP中,由等面积法得
DH=$\frac{AD.DP}{AP}$=$\frac{2DP}{\sqrt{4+DP²}}$,其中DPE(0,2)，　　(11分)
　所以DH=$\frac{2DP}{\sqrt{4+DP²}}$=2　$\sqrt{\frac{DP}{4+DP²}}$=2/$\sqrt{\frac{4}{4+DP²}}$1−　　　　E (0,$\sqrt{2}$)(题眼).　　　　　　　　　　　　　　　　(13分)
　设OC与平面ACP所成角为0，
　　　　$\frac{1}{2}$DH
　则sin0=oc=$\frac{DH}{2\sqrt{5}}$e(0,$\frac{\sqrt{10}}{10}$)(提示:根据几何法表示线面角的正弦值).　　　　　　　　　　　　　　　　(14分)
　所以OC与平面ACP所成角的正弦值的取值范围是。$\frac{10}{10}$　　　　　　　　　　　　　　　　　　　(15分)