第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
17. (15分)
抛掷甲、乙两枚质地均匀的骰子,所得的点数分别为$a$,$b$,记$\left[\frac{b}{a}\right]$的取值为随机变量$X$,其中$\left[\frac{b}{a}\right]$表示不超过$\frac{b}{a}$的最大整数.
(Ⅰ)求在$X\gt0$的条件下,$X=\frac{b}{a}$的概率;
(Ⅱ)求$X$的分布列及其数学期望.
答案:
条件概率+离散型随机变量的分布列及数学期望
解:(I)记抛掷骰子的样本点为(a,b),
则样本空间Ω={(a,b)×1≤a≤6,1≤b≤6,a∈Z,b∈Z},
则n(Ω)=36,
记事件A=“X>0”,记事件B=“X=$\frac{6}{a}$]−$\frac{b}{a}$”,
则A={(a,b)×1≤a≤b≤6,a∈Z,b∈Z},且n(A)=21,
(2分)
又AB={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),
(2,4),(2,6),(3,3),(3,6),(4,4),(5,5),(6,6))(提醒:在利
用列举法求基本事件时,注意要不重不漏),
=14, (4分)
)=$\frac{n(AB)}{n(A)}$=$\frac{14}{21}$=$\frac{2}{3}$,
条件下,X=$\frac{b}{a}$的概率为 (6分)
(II)X所有可能取值为0,1.2.3,4,5,6(题眼), (7分)
P(X=0)=$\frac{36−21}{36}$=$\frac{5}{12}$,P(X=1)=$\frac{12}{36}$=$\frac{1}{3}$,
P(X=2)=$\frac{4}{36}$=$\frac{1}{9}$,P(X=3)=$\frac{2}{36}$=$\frac{1}{18}$,
P(X=4)=$\frac{1}{36}$,P(X=5)=$\frac{1}{36}$,P(X=6)=$\frac{1}{36}$,
所以X的分布列为
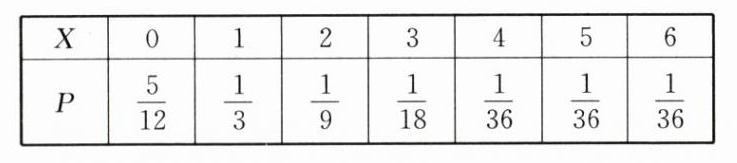
所以E(X)=0×$\frac{5}{12}$+1×$\frac{1}{3}$+2×$\frac{1}{9}$+3×$\frac{1}{18}$+4×$\frac{1}{36}$+5×$\frac{1}{36}$+6×$\frac{1}{36}$=4361′ (15分)
条件概率+离散型随机变量的分布列及数学期望
解:(I)记抛掷骰子的样本点为(a,b),
则样本空间Ω={(a,b)×1≤a≤6,1≤b≤6,a∈Z,b∈Z},
则n(Ω)=36,
记事件A=“X>0”,记事件B=“X=$\frac{6}{a}$]−$\frac{b}{a}$”,
则A={(a,b)×1≤a≤b≤6,a∈Z,b∈Z},且n(A)=21,
(2分)
又AB={(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,2),
(2,4),(2,6),(3,3),(3,6),(4,4),(5,5),(6,6))(提醒:在利
用列举法求基本事件时,注意要不重不漏),
=14, (4分)
)=$\frac{n(AB)}{n(A)}$=$\frac{14}{21}$=$\frac{2}{3}$,
条件下,X=$\frac{b}{a}$的概率为 (6分)
(II)X所有可能取值为0,1.2.3,4,5,6(题眼), (7分)
P(X=0)=$\frac{36−21}{36}$=$\frac{5}{12}$,P(X=1)=$\frac{12}{36}$=$\frac{1}{3}$,
P(X=2)=$\frac{4}{36}$=$\frac{1}{9}$,P(X=3)=$\frac{2}{36}$=$\frac{1}{18}$,
P(X=4)=$\frac{1}{36}$,P(X=5)=$\frac{1}{36}$,P(X=6)=$\frac{1}{36}$,
所以X的分布列为

所以E(X)=0×$\frac{5}{12}$+1×$\frac{1}{3}$+2×$\frac{1}{9}$+3×$\frac{1}{18}$+4×$\frac{1}{36}$+5×$\frac{1}{36}$+6×$\frac{1}{36}$=4361′ (15分)
18. (17分)
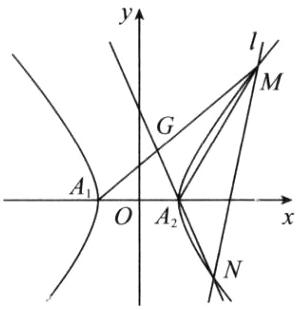
已知双曲线$C:\frac{x^{2}}{4}-y^{2}=1$的左、右顶点分别为$A_{1}$,$A_{2}$,过点$P(4,0)$的直线$l$与双曲线$C$的右支交于$M$,$N$两点.
(Ⅰ)若直线$l$的斜率$k$存在,求$k$的取值范围;
(Ⅱ)记直线$A_{1}M$,$A_{2}N$的斜率分别为$k_{1}$,$k_{2}$,求$\frac{k_{1}}{k_{2}}$的值;
(Ⅲ)设$G$为直线$A_{1}M$与直线$A_{2}N$的交点,$\triangle GMN$,$\triangle GA_{1}A_{2}$的面积分别为$S_{1}$,$S_{2}$,求$\frac{S_{1}}{S_{2}}$的最小值.
答案:
直线与双曲线的位置关系+双曲线中的面积问题
:[思维导图](I)设M(x1,y1),N(x2,y2),,直线l的方程;;1与双曲消线去方x程联立(m²−4)y²+8my+12=0列出不等式组{1 im的取值范围→k的取值范围. 11 ;(II)解法一,解法二:A1(−2,0),A2(2,0)结韦合达(定I理)y¹+|y2,y1y2斜率公式$\frac{k}{k2}$的表达式→得解;
;解法三:A1(−2,0),A2(2,0)
;1分直线/的斜率存在与不存在讨论$\frac{k}{k}$的表达式→得解. 11 ;(IIII)解法一,解法二:直线AlM与A2N的方程;:1联立直线方程xG三角形面积公式得解. 1 解:(I)设M(x1,y1),N(x2,y2),直线l的方程为x=my+4(技巧:在圆锥曲线中设直线方程时,若所设直线可以垂直于x轴,但不能垂直于y轴,即所设直线的斜率不能为0,则直接进行反设直线为x=ny十m(n,m为常数),这样可以避免分类讨论),
$\frac{x²}{4}$−y²=1,
联立{ 消去x,得(m²−4)y²+8my+12=0 x=my+4,
(题眼), (2分)
A=(8m)²−4(m²−4)×12=16(m²+12)>0,
则m²−4≠0, (易错:易y1y2=$\frac{12}{m²−4}$<0
{
天利忽略二次项的系数不能为0),
解得−2<m<2. (3分)
又斜率k存在,则m≠0且k=m1,
所以k的取值范围)U(,+∞)(另解:双曲(另解:双曲线C的渐近线方程为y=±$\frac{T}{2}$,显然直线1不能与两条渐近线平行,由双曲线的图象可知当k<一$\frac{1}{2}$或k>$\frac{1}{2}$时,直线l
与双曲线C的右支交于两点,因此k的取值范围是(−<8u,−$\frac{1}{2}$)U($\frac{1}{2}$,+∞)). (4分)
(II)解法一:由题意得A1(−2,0),A2(2,0).
结合(I)及韦达定理可知,
y1+y2=−$\frac{8m}{m²−4}$,y1y2=$\frac{12}{m²−4}$ (6分)
所以2my1y2=−3(y1+y2),
y1
所以$\frac{k}{k2}$=$\frac{x+2}{y2}$=$\frac{y(x2−2)}{y2(x+2)}$=$\frac{y(my2+2)}{y2(my+6)}$=$\frac{myy2+2y}{my1y2+6y2}$
x2−2
(8分)
一$\frac{3}{2}$(y1+y2)+2y1 $\frac{1}{2}$ $\frac{3}{2}$
=$\frac{2}{3}$ =$\frac{2}{39}$ . (10分)
一$\frac{3}{2}$(y1+y2)+6y2 −$\frac{3}{2}$y1 $\frac{9}{2}$y2
解法二:由题意得A1(−2,0),A2(2,0).
结合(I)及韦达定理可知,
y1+y2=−$\frac{8m}{m²−4}$,y1y2=$\frac{12}{m²−4}$. (6分)
.2
因为kMA,.kMA2=$\frac{y1}{x+2}$.$\frac{y}{x−2}$=$\frac{yi}{x²−4}$=$\frac{1}{4}$, (7分)
kMA.kNA=$\frac{yiy2}{(x−2)(x2−2)}$=$\frac{yiy2}{(my+2)(my2+2)}$
=$\frac{y1y2}{m²y1y2+2m(y+y2)+4}$ (8分)
$\frac{12}{m²−4}$
$\frac{m²−4}{12m²16m²}$=−$\frac{3}{4}$, (9分)
$\frac{12m²}{m²−4}$$\frac{16m²}{m²−4}$
1
所以$\frac{k}{k}$=$\frac{kMA.kMA}{RMA。.kNA}$=$\frac{4}{3}$ . (10分)
一$\frac{3}{4}$
解法三:由题意得A1(−2,0),A2(2,0).
当直线I的斜率k不存在时,不妨设M(4,,$\sqrt{3}$),N(4,−$\sqrt{3}$),于是k1=$\frac{\sqrt{3}}{6}$,k2=−$\frac{\sqrt{3}}{2}$,
则 $\frac{1}{3}$. (5分)
当直线Z的斜率k存在时,设直线/的方程为y=kx−4k,联立{$\frac{x}{4}$2−y²=1,消去y,整理得(4k²−1)x²²−32k²x+y=kx−4k,
64k²+4=0,易知k<−$\frac{1}{2}$或k>$\frac{1}{2}$,
由韦达定理可知x1+x2=$\frac{32k²}{4k²−1}$,x1x2=$\frac{64k²+4}{4k²−1}$, (7分)
所以x1x2=2(x1+x2)+$\frac{4}{4k²−1}$,
y1
所以$\frac{k}{k2}$=$\frac{x+2}{y2}$=$\frac{y(x2−2)}{y2(x+2)}$=$\frac{(k.x1−4k)(x2−2)}{(kx2−4k)(x+2)}$
x2−2
=$\frac{xx2−2x−4x2+8}{xx2−4x+2x2−8}$ (9分)
$\frac{4}{4k²−1}$− −
=$\frac{4k²−1}{4}$
x1+x2 $\frac{4}{4k²−1}$−4.x1 2−
−x2+$\frac{16k²−2}{4k²−1}$
=
−x1+2x2+$\frac{−16k²+6}{4k²−1}$
−($\frac{32k²}{4k²−1}$−x1)+$\frac{16k²−2}{4k²−1}$
=
−x1+22($\frac{32k²}{4k²−1}$−x1)+$\frac{−16k²+6}{4k²−−1}$
x1−$\frac{16k²+2}{4k²−1}$
=
−3x1+$\frac{48k²+6}{4k²−1}$
. (10分)
(III)解法一:由(II)可知k2=−3k1,
所以直线A1M与直线A2N的方程分别为y=k(x+2),y=−3k1(x−2), (11分)
联立两直线方程可得交点G的横坐标xG=1, (13分)
$\frac{1}{2}$|GM|.|GN|sin∠MGN
所以$\frac{S,}{S2}$= =$\frac{|GM}{|GA}$.$\frac{|GN|}{|GA}$
$\frac{1}{2}$|GA1|.|GA2|SsinA1GA
(关键:根据两角互补其正弦值相等,将面积比转化为边的比)
(15分)
=$\frac{x−1}{3}$.x21−1=$\frac{(my+3)(my2+3)}{3}$
=$\frac{m²y1y2+3m(y+y2)+9}{3}$
=$\frac{−m²−12}{m²−4}$=−1+$\frac{16}{4−m²}$
≥−1+$\frac{16}{4−0}$=3(方法:求解圆锥曲线的最值问题,当题目给出的条件和结论的几何特征不明显时,可以建立目标函数,求目标函数的最值(或值域),常用方法:①配方法;②基本不等式;③单调性法;④三角换元法;⑤导数法等,要特别注意自变量的取值范围),
故$\frac{S}{S2}$的最小值为3,当且仅当m=0时等号成立. (17分)
解法二:直线A1M与直线A2N的方程分别为y=$\frac{y}{x+2}$.
(x+2),y=$\frac{y2}{x2−2}$(x−2), (11分)
联立两直线方程,利用2myiy2=−3(y1+y2)可得交点G的
横坐标
xG=$\frac{2xy2+2x2y+4y2−4y}{x1y2−x2y1+2y2+2y}$
=2(my1+4)y2+2(my2+4)y1+4y2−4y1
(my1+4)y2−(my2+4)y1+2y2+2y1
=$\frac{2myy2+6y2+2y}{3y2−y}$
=$\frac{−3(y+y2)+6y2+2y}{3y2−y}$
=1, (13分)
$\frac{1}{2}$|GM|.|GN|sin∠MGN
所以$\frac{S}{S2}$− =$\frac{|GM|}{|GA}$.$\frac{IGN|}{|GA}$
$\frac{1}{2}$|GA1|.|GA2|sin∠AGA2
(15分)
=$\frac{x−1}{3}$.x21−1=$\frac{(my+3)(my2+3)}{3}$
=$\frac{m²y1y2+3m(y+y2)+9}{3}$
=$\frac{−m²−12}{m²−4}$=−1+$\frac{16}{4−m²}$
≥−1+$\frac{16}{4−0
直线与双曲线的位置关系+双曲线中的面积问题
:[思维导图](I)设M(x1,y1),N(x2,y2),,直线l的方程;;1与双曲消线去方x程联立(m²−4)y²+8my+12=0列出不等式组{1 im的取值范围→k的取值范围. 11 ;(II)解法一,解法二:A1(−2,0),A2(2,0)结韦合达(定I理)y¹+|y2,y1y2斜率公式$\frac{k}{k2}$的表达式→得解;
;解法三:A1(−2,0),A2(2,0)
;1分直线/的斜率存在与不存在讨论$\frac{k}{k}$的表达式→得解. 11 ;(IIII)解法一,解法二:直线AlM与A2N的方程;:1联立直线方程xG三角形面积公式得解. 1 解:(I)设M(x1,y1),N(x2,y2),直线l的方程为x=my+4(技巧:在圆锥曲线中设直线方程时,若所设直线可以垂直于x轴,但不能垂直于y轴,即所设直线的斜率不能为0,则直接进行反设直线为x=ny十m(n,m为常数),这样可以避免分类讨论),
$\frac{x²}{4}$−y²=1,
联立{ 消去x,得(m²−4)y²+8my+12=0 x=my+4,
(题眼), (2分)
A=(8m)²−4(m²−4)×12=16(m²+12)>0,
则m²−4≠0, (易错:易y1y2=$\frac{12}{m²−4}$<0
{
天利忽略二次项的系数不能为0),
解得−2<m<2. (3分)
又斜率k存在,则m≠0且k=m1,
所以k的取值范围)U(,+∞)(另解:双曲(另解:双曲线C的渐近线方程为y=±$\frac{T}{2}$,显然直线1不能与两条渐近线平行,由双曲线的图象可知当k<一$\frac{1}{2}$或k>$\frac{1}{2}$时,直线l
与双曲线C的右支交于两点,因此k的取值范围是(−<8u,−$\frac{1}{2}$)U($\frac{1}{2}$,+∞)). (4分)
(II)解法一:由题意得A1(−2,0),A2(2,0).
结合(I)及韦达定理可知,
y1+y2=−$\frac{8m}{m²−4}$,y1y2=$\frac{12}{m²−4}$ (6分)
所以2my1y2=−3(y1+y2),
y1
所以$\frac{k}{k2}$=$\frac{x+2}{y2}$=$\frac{y(x2−2)}{y2(x+2)}$=$\frac{y(my2+2)}{y2(my+6)}$=$\frac{myy2+2y}{my1y2+6y2}$
x2−2
(8分)
一$\frac{3}{2}$(y1+y2)+2y1 $\frac{1}{2}$ $\frac{3}{2}$
=$\frac{2}{3}$ =$\frac{2}{39}$ . (10分)
一$\frac{3}{2}$(y1+y2)+6y2 −$\frac{3}{2}$y1 $\frac{9}{2}$y2
解法二:由题意得A1(−2,0),A2(2,0).
结合(I)及韦达定理可知,
y1+y2=−$\frac{8m}{m²−4}$,y1y2=$\frac{12}{m²−4}$. (6分)
.2
因为kMA,.kMA2=$\frac{y1}{x+2}$.$\frac{y}{x−2}$=$\frac{yi}{x²−4}$=$\frac{1}{4}$, (7分)
kMA.kNA=$\frac{yiy2}{(x−2)(x2−2)}$=$\frac{yiy2}{(my+2)(my2+2)}$
=$\frac{y1y2}{m²y1y2+2m(y+y2)+4}$ (8分)
$\frac{12}{m²−4}$
$\frac{m²−4}{12m²16m²}$=−$\frac{3}{4}$, (9分)
$\frac{12m²}{m²−4}$$\frac{16m²}{m²−4}$
1
所以$\frac{k}{k}$=$\frac{kMA.kMA}{RMA。.kNA}$=$\frac{4}{3}$ . (10分)
一$\frac{3}{4}$
解法三:由题意得A1(−2,0),A2(2,0).
当直线I的斜率k不存在时,不妨设M(4,,$\sqrt{3}$),N(4,−$\sqrt{3}$),于是k1=$\frac{\sqrt{3}}{6}$,k2=−$\frac{\sqrt{3}}{2}$,
则 $\frac{1}{3}$. (5分)
当直线Z的斜率k存在时,设直线/的方程为y=kx−4k,联立{$\frac{x}{4}$2−y²=1,消去y,整理得(4k²−1)x²²−32k²x+y=kx−4k,
64k²+4=0,易知k<−$\frac{1}{2}$或k>$\frac{1}{2}$,
由韦达定理可知x1+x2=$\frac{32k²}{4k²−1}$,x1x2=$\frac{64k²+4}{4k²−1}$, (7分)
所以x1x2=2(x1+x2)+$\frac{4}{4k²−1}$,
y1
所以$\frac{k}{k2}$=$\frac{x+2}{y2}$=$\frac{y(x2−2)}{y2(x+2)}$=$\frac{(k.x1−4k)(x2−2)}{(kx2−4k)(x+2)}$
x2−2
=$\frac{xx2−2x−4x2+8}{xx2−4x+2x2−8}$ (9分)
$\frac{4}{4k²−1}$− −
=$\frac{4k²−1}{4}$
x1+x2 $\frac{4}{4k²−1}$−4.x1 2−
−x2+$\frac{16k²−2}{4k²−1}$
=
−x1+2x2+$\frac{−16k²+6}{4k²−1}$
−($\frac{32k²}{4k²−1}$−x1)+$\frac{16k²−2}{4k²−1}$
=
−x1+22($\frac{32k²}{4k²−1}$−x1)+$\frac{−16k²+6}{4k²−−1}$
x1−$\frac{16k²+2}{4k²−1}$
=
−3x1+$\frac{48k²+6}{4k²−1}$
. (10分)
(III)解法一:由(II)可知k2=−3k1,
所以直线A1M与直线A2N的方程分别为y=k(x+2),y=−3k1(x−2), (11分)
联立两直线方程可得交点G的横坐标xG=1, (13分)
$\frac{1}{2}$|GM|.|GN|sin∠MGN
所以$\frac{S,}{S2}$= =$\frac{|GM}{|GA}$.$\frac{|GN|}{|GA}$
$\frac{1}{2}$|GA1|.|GA2|SsinA1GA
(关键:根据两角互补其正弦值相等,将面积比转化为边的比)
(15分)
=$\frac{x−1}{3}$.x21−1=$\frac{(my+3)(my2+3)}{3}$
=$\frac{m²y1y2+3m(y+y2)+9}{3}$
=$\frac{−m²−12}{m²−4}$=−1+$\frac{16}{4−m²}$
≥−1+$\frac{16}{4−0}$=3(方法:求解圆锥曲线的最值问题,当题目给出的条件和结论的几何特征不明显时,可以建立目标函数,求目标函数的最值(或值域),常用方法:①配方法;②基本不等式;③单调性法;④三角换元法;⑤导数法等,要特别注意自变量的取值范围),
故$\frac{S}{S2}$的最小值为3,当且仅当m=0时等号成立. (17分)

解法二:直线A1M与直线A2N的方程分别为y=$\frac{y}{x+2}$.
(x+2),y=$\frac{y2}{x2−2}$(x−2), (11分)
联立两直线方程,利用2myiy2=−3(y1+y2)可得交点G的
横坐标
xG=$\frac{2xy2+2x2y+4y2−4y}{x1y2−x2y1+2y2+2y}$
=2(my1+4)y2+2(my2+4)y1+4y2−4y1
(my1+4)y2−(my2+4)y1+2y2+2y1
=$\frac{2myy2+6y2+2y}{3y2−y}$
=$\frac{−3(y+y2)+6y2+2y}{3y2−y}$
=1, (13分)
$\frac{1}{2}$|GM|.|GN|sin∠MGN
所以$\frac{S}{S2}$− =$\frac{|GM|}{|GA}$.$\frac{IGN|}{|GA}$
$\frac{1}{2}$|GA1|.|GA2|sin∠AGA2
(15分)
=$\frac{x−1}{3}$.x21−1=$\frac{(my+3)(my2+3)}{3}$
=$\frac{m²y1y2+3m(y+y2)+9}{3}$
=$\frac{−m²−12}{m²−4}$=−1+$\frac{16}{4−m²}$
≥−1+$\frac{16}{4−0
19. (17分)
在空间直角坐标系$O - xyz$中,任一平面的方程都能表示成$Ax + By + Cz + D = 0$,其中$A$,$B$,$C$,$D\in\mathbf{R}$,$A^{2}+B^{2}+C^{2}\neq0$,且$\boldsymbol{n}=(A,B,C)$为该平面的法向量.
已知集合$P = \{ (x,y,z)||x|\leqslant1,|y|\leqslant1,|z|\leqslant1\}$,
$Q = \{ (x,y,z)||x|+|y|+|z|\leqslant2\}$,
$T = \{ (x,y,z)||x|+|y|\leqslant2,|y|+|z|\leqslant2,|z|+|x|\leqslant2\}$.
(Ⅰ)设集合$M = \{ (x,y,z)|z = 0\}$,记$P\cap M$中所有点构成的图形的面积为$S_{1}$,$Q\cap M$中所有点构成的图形的面积为$S_{2}$,求$S_{1}$和$S_{2}$的值;
(Ⅱ)记集合$Q$中所有点构成的几何体的体积为$V_{1}$,$P\cap Q$中所有点构成的几何体的体积为$V_{2}$,求$V_{1}$和$V_{2}$的值;
(Ⅲ)记集合$T$中所有点构成的几何体为$W$.
①求$W$的体积$V_{3}$的值;
②求$W$的相邻(有公共棱)两个面所成二面角的大小,并指出$W$的面数和棱数.
答案:
立体几何中的新定义问题+多面体的体积 【思维导图】(Ⅰ)已知条件→集合\(M\),\(P\),\(Q\)代表的点→\(P\cap M\),\(Q\cap M\)代表的点→\(S_{1}\),\(S_{2}\)→得解. (Ⅱ)记集合\(Q\)的子集\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\)→\(V_{Q'}\)→\(V_{1}\)→记集合\(P\)的子集\(P'=\{(x,y,z)|0\leqslant x\leqslant1,0\leqslant y\leqslant1,0\leqslant z\leqslant1\}\)→\(P'\cap Q'\)为\(P'\)截去三棱锥\(Q_{4}-Q_{1}Q_{2}Q_{3}\)所剩下的部分→\(V_{P'\cap Q'}\)→\(V_{2}\)→得解. (Ⅲ)①解法一:已知条件→\(V_{E - ABCD}\)→\(V_{3}\); 解法二:记集合\(T\)的子集\(T'\)→\(B\),\(C\),\(D\)各点坐标→\(V_{T'}\)→\(V_{3}\). ②两平面的法向量→空间夹角公式→二面角的大小→\(W\)的面数和棱数→得解. 解:(Ⅰ)集合\(M=\{(x,y,z)|z = 0\}\)表示\(xOy\)平面上所有的点,\(P=\{(x,y,z)||x|\leqslant1,|y|\leqslant1,|z|\leqslant1\}\)表示\((\pm1,\pm1,\pm1)\)这八个顶点形成的正方体内所有的点,\(P\cap M\)可以看成正方体在\(xOy\)平面上的截面内所有的点,它是边长为2的正方形(关键:判断出截面的形状),因此\(S_{1}=4\). (2分) 对于\(Q=\{(x,y,z)||x|+|y|+|z|\leqslant2\}\),当\(x,y,z\gt0\)时,\(x + y + z = 2\)表示经过点\((2,0,0)\),\((0,2,0)\),\((0,0,2)\)的平面在第一象限的部分. 由对称性可知\(Q\)表示\((\pm2,0,0)\),\((0,\pm2,0)\),\((0,0,\pm2)\)这六个顶点形成的正八面体内所有的点,\(Q\cap M\)可以看成正八面体在\(xOy\)平面上的截面内所有的点,它是边长为\(2\sqrt{2}\)的正方形,因此\(S_{2}=8\). (4分) (Ⅱ)由题知,集合\(Q\),\(P\cap Q\)中所有点构成的几何体的体积分别为\(V_{1}\),\(V_{2}\),记集合\(Q\)的子集\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\),即为三个坐标平面与\(x + y + z = 2\)围成的四面体,四面体四个顶点分别为\((0,0,0)\),\((2,0,0)\),\((0,2,0)\),\((0,0,2)\),此四面体的体积\(V_{Q'}=\frac{1}{3}\times2\times(\frac{1}{2}\times2\times2)=\frac{4}{3}\),由对称性知,\(V_{1}=8V_{Q'}=\frac{32}{3}\). (6分) 记集合\(P\)的子集\(P'\)构成的几何体为棱长为1的正方体,即\(P'=\{(x,y,z)|0\leqslant x\leqslant1,0\leqslant y\leqslant1,0\leqslant z\leqslant1\}\),\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\),\(P'\cap Q'\)为两个几何体公共部分. 记\(Q_{1}(1,1,0)\),\(Q_{2}(1,0,1)\),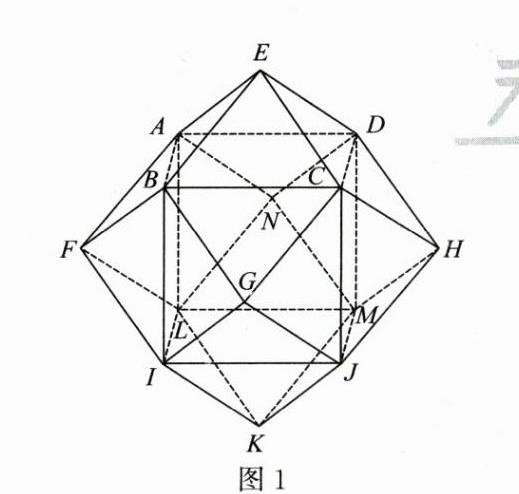

立体几何中的新定义问题+多面体的体积 【思维导图】(Ⅰ)已知条件→集合\(M\),\(P\),\(Q\)代表的点→\(P\cap M\),\(Q\cap M\)代表的点→\(S_{1}\),\(S_{2}\)→得解. (Ⅱ)记集合\(Q\)的子集\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\)→\(V_{Q'}\)→\(V_{1}\)→记集合\(P\)的子集\(P'=\{(x,y,z)|0\leqslant x\leqslant1,0\leqslant y\leqslant1,0\leqslant z\leqslant1\}\)→\(P'\cap Q'\)为\(P'\)截去三棱锥\(Q_{4}-Q_{1}Q_{2}Q_{3}\)所剩下的部分→\(V_{P'\cap Q'}\)→\(V_{2}\)→得解. (Ⅲ)①解法一:已知条件→\(V_{E - ABCD}\)→\(V_{3}\); 解法二:记集合\(T\)的子集\(T'\)→\(B\),\(C\),\(D\)各点坐标→\(V_{T'}\)→\(V_{3}\). ②两平面的法向量→空间夹角公式→二面角的大小→\(W\)的面数和棱数→得解. 解:(Ⅰ)集合\(M=\{(x,y,z)|z = 0\}\)表示\(xOy\)平面上所有的点,\(P=\{(x,y,z)||x|\leqslant1,|y|\leqslant1,|z|\leqslant1\}\)表示\((\pm1,\pm1,\pm1)\)这八个顶点形成的正方体内所有的点,\(P\cap M\)可以看成正方体在\(xOy\)平面上的截面内所有的点,它是边长为2的正方形(关键:判断出截面的形状),因此\(S_{1}=4\). (2分) 对于\(Q=\{(x,y,z)||x|+|y|+|z|\leqslant2\}\),当\(x,y,z\gt0\)时,\(x + y + z = 2\)表示经过点\((2,0,0)\),\((0,2,0)\),\((0,0,2)\)的平面在第一象限的部分. 由对称性可知\(Q\)表示\((\pm2,0,0)\),\((0,\pm2,0)\),\((0,0,\pm2)\)这六个顶点形成的正八面体内所有的点,\(Q\cap M\)可以看成正八面体在\(xOy\)平面上的截面内所有的点,它是边长为\(2\sqrt{2}\)的正方形,因此\(S_{2}=8\). (4分) (Ⅱ)由题知,集合\(Q\),\(P\cap Q\)中所有点构成的几何体的体积分别为\(V_{1}\),\(V_{2}\),记集合\(Q\)的子集\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\),即为三个坐标平面与\(x + y + z = 2\)围成的四面体,四面体四个顶点分别为\((0,0,0)\),\((2,0,0)\),\((0,2,0)\),\((0,0,2)\),此四面体的体积\(V_{Q'}=\frac{1}{3}\times2\times(\frac{1}{2}\times2\times2)=\frac{4}{3}\),由对称性知,\(V_{1}=8V_{Q'}=\frac{32}{3}\). (6分) 记集合\(P\)的子集\(P'\)构成的几何体为棱长为1的正方体,即\(P'=\{(x,y,z)|0\leqslant x\leqslant1,0\leqslant y\leqslant1,0\leqslant z\leqslant1\}\),\(Q'=\{(x,y,z)|x + y + z\leqslant2,x\geqslant0,y\geqslant0,z\geqslant0\}\),\(P'\cap Q'\)为两个几何体公共部分. 记\(Q_{1}(1,1,0)\),\(Q_{2}(1,0,1)\),


查看更多完整答案,请扫码查看


