第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
10.函数f((x))=ccoSs(πx+))(<<∝<$\frac{π}{2}${的部分图象如图所示,下列结论正确的是 ( 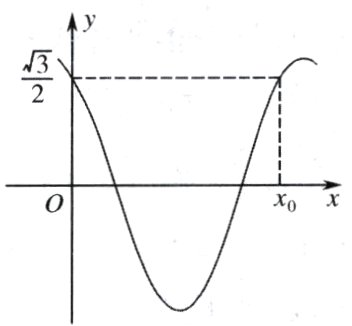
A.=$\frac{π}{6}$
B.x0=$\frac{5}{3}$
C.f(x)的图象的一个对称中心为($\frac{17}{6}$,0
D.设函数g(x)=f(x)+f(x+$\frac{1}{3}$),则g(x))在
[|$\frac{1}{2}$,$\frac{1}{3}${上的最小值为一$\frac{\sqrt{3}}{2}$

A.=$\frac{π}{6}$
B.x0=$\frac{5}{3}$
C.f(x)的图象的一个对称中心为($\frac{17}{6}$,0
D.设函数g(x)=f(x)+f(x+$\frac{1}{3}$),则g(x))在
[|$\frac{1}{2}$,$\frac{1}{3}${上的最小值为一$\frac{\sqrt{3}}{2}$
答案:
ABD
11.定义在R上的偶函数f(x)满足f(x−3)=
f(5−x),当x∈[0,1]时,f(x)=x².设函数g(x)=logs|x−1l,则下列结论正确的是(
A.f(x)的图象关于直线x=1对称
B.f(x)的图象在x=$\frac{7}{2}$处的切线方程为y=
−x+$\frac{17}{4}$
C.f(2021)+f(2022)+f(2023)+f(2024)=2
D.f(x)的图象与g(x)的图象所有交点的横坐标之和为10
f(5−x),当x∈[0,1]时,f(x)=x².设函数g(x)=logs|x−1l,则下列结论正确的是(
A.f(x)的图象关于直线x=1对称
B.f(x)的图象在x=$\frac{7}{2}$处的切线方程为y=
−x+$\frac{17}{4}$
C.f(2021)+f(2022)+f(2023)+f(2024)=2
D.f(x)的图象与g(x)的图象所有交点的横坐标之和为10
答案:
ACD
ACD

三、填空题:本题共3小题,每小题5分,共15分
12.已知tanα=2,则sinα.cosα=
12.已知tanα=2,则sinα.cosα=
答案:
$\frac{2}{5}$ 同角三角函数的基本关系 通解:由$\tan\alpha = \frac{\sin\alpha}{\cos\alpha} = 2$,$\sin^{2}\alpha + \cos^{2}\alpha = 1$,解得$\begin{cases}\sin\alpha = \frac{2\sqrt{5}}{5}\\\cos\alpha = \frac{\sqrt{5}}{5}\end{cases}$或$\begin{cases}\sin\alpha = -\frac{2\sqrt{5}}{5}\\\cos\alpha = -\frac{\sqrt{5}}{5}\end{cases}$,$\therefore \sin\alpha\cdot\cos\alpha = \frac{2}{5}$. 快解:$\sin\alpha\cdot\cos\alpha = \frac{\sin\alpha\cdot\cos\alpha}{\sin^{2}\alpha + \cos^{2}\alpha} = \frac{\tan\alpha}{\tan^{2}\alpha + 1} = \frac{2}{4 + 1} = \frac{2}{5}$.
13.洛卡斯是十九世纪法国数学家,他以研究斐波那契数列而著名.洛卡斯数列就是以他的名字命名,洛卡斯数列{L}为:1,3,4,7,11,18,29,47,76,.….,即L1=1,L2=3,且Ln+2=Ln+1+Ln (n∈N).设数列{L,}各项依次除以4所得余数形成的数列为{a,},则a10)=________.
答案:
3
14.已知抛物线方程y=$\frac{x²}{4}$,经过焦点F斜率为k(k≠0)的直线交抛物线于A,B两点,线段
AB的垂直平分线交y轴于点C,则$\frac{|AB|}{|CF}$的值为________.
AB的垂直平分线交y轴于点C,则$\frac{|AB|}{|CF}$的值为________.
答案:
2
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
某兴趣小组,对高三刚结束的测试的物理成绩进行随机调查,在所有选择物理科的考生中随机抽取100名各类考生的物理成绩,整理数据如表(单位:人).
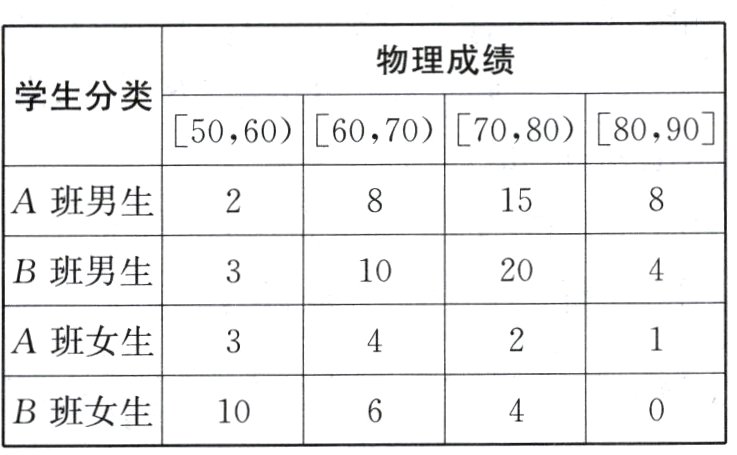
(I)估计该校高三学习物理男生人数与女生人数的比值;
(II)求A班物理平均成绩的估计值(同一组中的数据用该组区间中点值为代表,结果四舍五入到整数);
(III)把成绩在[60,90]称为及格,成绩在[50,60)
为不及格,根据所有数据完成下面2×2列联表,试根据小概率值α=0.01的独立性检验,分析该校考生的物理成绩与性别是否有关?
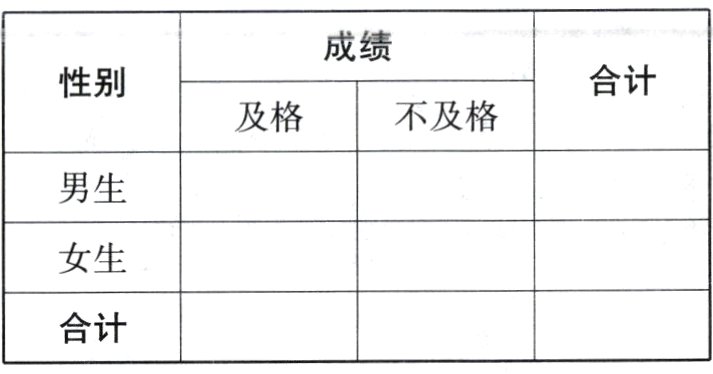
x²=$\frac{n(ad−bc)²}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.

15.(13分)
某兴趣小组,对高三刚结束的测试的物理成绩进行随机调查,在所有选择物理科的考生中随机抽取100名各类考生的物理成绩,整理数据如表(单位:人).

(I)估计该校高三学习物理男生人数与女生人数的比值;
(II)求A班物理平均成绩的估计值(同一组中的数据用该组区间中点值为代表,结果四舍五入到整数);
(III)把成绩在[60,90]称为及格,成绩在[50,60)
为不及格,根据所有数据完成下面2×2列联表,试根据小概率值α=0.01的独立性检验,分析该校考生的物理成绩与性别是否有关?

x²=$\frac{n(ad−bc)²}{(a+b)(c+d)(a+c)(b+d)}$,n=a+b+c+d.

答案:
平均数 + 独立性检验 解:(Ⅰ)由题表中数据可知,男生共有$2 + 8 + 15 + 8 + 3 + 10 + 20 + 4 = 70$(人),女生共有$3 + 4 + 2 + 1 + 10 + 6 + 4 + 0 = 30$(人). (2 分) 由此估计该校高三学习物理男生人数与女生人数的比值约为$\frac{7}{3}$. (3 分) (Ⅱ)$A$班共有$2 + 3 + 8 + 4 + 15 + 2 + 8 + 1 = 43$(人), (5 分) $A$班物理平均成绩的估计值为$55\times\frac{5}{43} + 65\times\frac{12}{43} + 75\times\frac{17}{43} + 85\times\frac{9}{43} = \frac{275 + 780 + 1275 + 765}{43}\approx 72$(提示:加权平均数的计算公式). (7 分) (Ⅲ)补全$2\times 2$列联表如表所示. | 性别 | 成绩 | | 合计 | | ---- | ---- | ---- | ---- | | | 及格 | 不及格 | | | 男生 | 65 | 5 | 70 | | 女生 | 17 | 13 | 30 | | 合计 | 82 | 18 | 100 | (9 分) 零假设为$H_{0}$:该校考生的物理成绩与性别无关,根据表格中数据计算得到$\chi^{2} = \frac{100\times(65\times13 - 5\times17)^{2}}{70\times30\times82\times18}\approx 18.635\gt 6.635 = x_{0.01}$(题眼). (12 分) 根据小概率值$\alpha = 0.01$的独立性检验,推断$H_{0}$不成立,即认为该校考生的物理成绩与性别有关,此推断犯错误的概率不大于 0.01. (13 分)
查看更多完整答案,请扫码查看


