第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
18. (17分)
在平面直角坐标系内,以原点$O$为圆心,$a$,$b(a>0,b>0,a,b$为定值$)$为半径分别作同心圆$C_{1}$,$C_{2}$,设$A$为圆$C_{1}$上任一点(不在$y$轴上),作直线$OA$,过点$A$作圆$C_{1}$的切线$AA'$与$x$轴交于点$A'$,过圆$C_{2}$与$x$轴的交点$B$作圆$C_{2}$的切线$BB'$与直线$OA$交于点$B'$,过点$A'$,$B'$分别作$x$轴,$y$轴的垂线$A'M$,$B'M$交于点$M$.
(Ⅰ)求动点$M$的轨迹$E$的方程;
(Ⅱ)设$c=\sqrt{a^{2}+b^{2}}$,点$F_{1}(-c,0)$,$F_{2}(c,0)$,过点$F_{1}$的直线与轨迹$E$交于$A$,$B$两点(两点均在$y$轴左侧).
(ⅰ)若$\angle AF_{2}B=\frac{\pi}{2}$,$\triangle AF_{2}B$的内切圆的圆心的纵坐标为$\sqrt{3}a$,求$\frac{c}{a}$的值;
(ⅱ)若点$P$是曲线$E$上($y$轴左侧)的点,过点$O$作直线与曲线$E$在$P$处的切线平行,交$PF_{2}$于点$Q$,证明:$PQ$的长为定值.
在平面直角坐标系内,以原点$O$为圆心,$a$,$b(a>0,b>0,a,b$为定值$)$为半径分别作同心圆$C_{1}$,$C_{2}$,设$A$为圆$C_{1}$上任一点(不在$y$轴上),作直线$OA$,过点$A$作圆$C_{1}$的切线$AA'$与$x$轴交于点$A'$,过圆$C_{2}$与$x$轴的交点$B$作圆$C_{2}$的切线$BB'$与直线$OA$交于点$B'$,过点$A'$,$B'$分别作$x$轴,$y$轴的垂线$A'M$,$B'M$交于点$M$.
(Ⅰ)求动点$M$的轨迹$E$的方程;
(Ⅱ)设$c=\sqrt{a^{2}+b^{2}}$,点$F_{1}(-c,0)$,$F_{2}(c,0)$,过点$F_{1}$的直线与轨迹$E$交于$A$,$B$两点(两点均在$y$轴左侧).
(ⅰ)若$\angle AF_{2}B=\frac{\pi}{2}$,$\triangle AF_{2}B$的内切圆的圆心的纵坐标为$\sqrt{3}a$,求$\frac{c}{a}$的值;
(ⅱ)若点$P$是曲线$E$上($y$轴左侧)的点,过点$O$作直线与曲线$E$在$P$处的切线平行,交$PF_{2}$于点$Q$,证明:$PQ$的长为定值.
答案:
直线与圆的位置关系+直线与圆锥曲线的综合应用 解:(Ⅰ)设$A(x_0,y_0)$,则$x_0^2 + y_0^2 = a^2$. (1 分)过点$A$的切线方程为$x_0x + y_0y = a^2$,所以$A'(\frac{a^2}{x_0},0)$,(2 分)由直线$OA:y = \frac{y_0}{x_0}x$和切线$BB':x = \pm b$,得$B'(\pm b,\pm\frac{y_0}{x_0}b)$(关键:由已知条件求出点$A'$,$B'$的坐标是解题关键). (3 分)设$M(x,y)$,则$\begin{cases}x = \frac{a^2}{x_0}\\y = \pm\frac{y_0}{x_0}b\end{cases}$,即$\begin{cases}x_0 = \frac{a^2}{x}\\y_0 = \pm\frac{a^2y}{bx}\end{cases}$. (4 分)由$x_0^2 + y_0^2 = a^2$,得$\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$即为所求$E$的方程. (5 分) (Ⅱ)设$\triangle AF_2B$内切圆圆心为$S$,点$G$,$H$,$J$分别为圆与$AF_2$,$BF_2$,$AB$的切点. (ⅰ)由(Ⅰ)可知,轨迹$E$是以$F_1$,$F_2$为焦点的双曲线,由双曲线定义可知$|AF_2| = |AF_1| + 2a$,$|BF_2| = |BF_1| + 2a$,且$|AF_1| + |BF_1| = |AB|$. (6 分)由$\angle AF_2B = \frac{\pi}{2}$,有$|AF_2| + |BF_2| - |AB| = 2r$(提示:直角三角形内切圆半径公式),$r$为内切圆$S$的半径(题眼). (7 分)从而$|AF_2| + |BF_2| - |AB| = 2r = |AF_1| + 2a + |BF_1| + 2a - |AB|$,有$2r = 4a$. (8 分)又$|AF_2| - |AF_1| = 2a = r$,所以内切圆与$AB$边的切点与$F_1$重合,设内切圆圆心$S(s,\sqrt{3}a)$,有$|SF_1| = 2a$,$|SF_2| = 2\sqrt{2}a$. (9 分)联立有$\begin{cases}s + c = a\\c - s = \sqrt{5}a\end{cases}$,所以$\frac{c}{a} = \frac{\sqrt{5} + 1}{2}$. (10 分) (ⅱ)证明:设$P(x_0,y_0)$,过点$P$作$\angle F_1PF_2$的平分线,交$x$轴于点$T$,设$T(m,0)$,$|PF_1| = -a - \frac{c}{a}x_0$,$|PF_2| = a - \frac{c}{a}x_0$(提示:双曲线的焦半径公式),由角平分线定理得$\frac{|PF_1|}{|PF_2|} = \frac{|TF_1|}{|TF_2|}$,即$\frac{-a - \frac{c}{a}x_0}{a - \frac{c}{a}x_0} = \frac{m + c}{c - m}$,解得$m = \frac{a^2}{x_0}$,(11 分)从而$k_{PT} = \frac{y_0}{x_0 - \frac{a^2}{x_0}} = \frac{x_0y_0}{x_0^2 - a^2} = \frac{x_0y_0}{\frac{a^2y_0^2}{b^2}} = \frac{b^2x_0}{a^2y_0}$. (12 分)设过点$P$的切线方程为$y - y_0 = k(x - x_0)$,与双曲线方程联立,解得$k = \frac{b^2x_0}{a^2y_0}$,所以切线即为$PT$,(13 分)延长$F_1P$至$R$,使得$|PR| = |PF_2|$,连接$RF_2$,则$RF_2\parallel PT$,设过坐标原点$O$且与$P$处切线平行的直线与$PF_1$交于点$W$,$|PW| = |PQ|$,由于$O$为$F_1F_2$中点,所以$W$为$RF_1$中点,又$|RW| = |QF_2|$,所以$|WF_1| = |QF_2|$,(15 分)从而$2a = |PF_2| - |PF_1| = |PR| - |PF_1| = |PR| - (|WF_1| - |PW|) = |PR| - |RW| + |PW| = |PW| + |PW| = 2|PQ|$,所以$|PQ| = a$,即$PQ$的长为定值. (17 分)
19. (17分)
设$(X,Y)$的所有可能取值为$(x_{i},y_{j})$,称$p_{ij}=P(X = x_{i},Y = y_{j})(i = 1,2,\cdots,n,j = 1,2,\cdots,m)$为二维离散随机变量$(X,Y)$的联合分布列,用表格表示为:
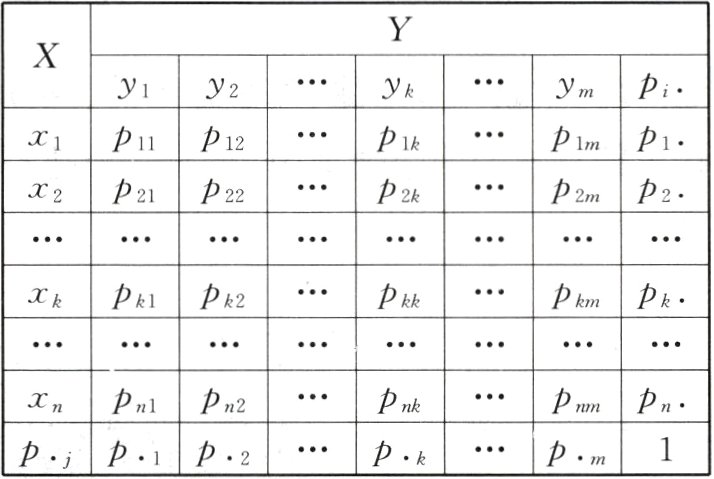
仿照条件概率的定义,有如下离散随机变量的条件分布列:定义$P(Y = y_{j})=p_{·j}=\sum_{i = 1}^{n}p_{ij}$.对于固定的$j$,若$p_{·j}>0$,则称$p_{i|j}=P(X = x_{i}|Y = y_{j})=\frac{p_{ij}}{p_{·j}}(i = 1,2,\cdots,n)$为给定$Y = y_{j}$条件下的$X$条件分布列.
离散随机变量的条件分布的数学期望(若存在)定义如下:$E(X|Y = y)=\sum_{i = 1}^{n}x_{i}P(X = x_{i}|Y = y)$.
(Ⅰ)设二维离散随机变量$(X,Y)$的联合分布列为
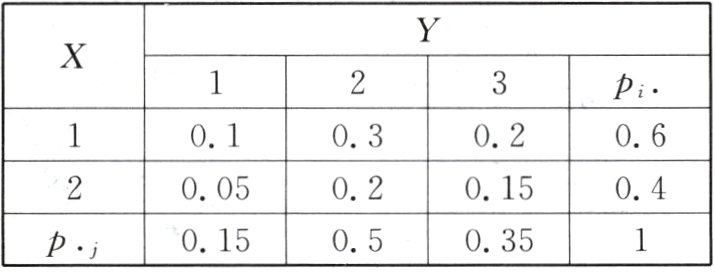
求给定$X = 1$条件下的$Y$条件分布列;
(Ⅱ)设$(X,Y)$为二维离散随机变量,且$E(X)$存在,证明:$E(X)=\sum_{j = 1}^{m}E(X|Y = y_{j})\cdot p_{·j}$;
(Ⅲ)某人被困在有三个门的迷宫里,第一个门通向离开迷宫的道,沿此道走30分钟可走出迷宫;第二个门通一条迷道,沿此迷道走50分钟又回到原处;第三个门通一条迷道,沿此迷道走70分钟也回到原处,假定此人总是等可能地在三个门中选择一个,试求他平均要用多少时间才能走出迷宫.
设$(X,Y)$的所有可能取值为$(x_{i},y_{j})$,称$p_{ij}=P(X = x_{i},Y = y_{j})(i = 1,2,\cdots,n,j = 1,2,\cdots,m)$为二维离散随机变量$(X,Y)$的联合分布列,用表格表示为:

仿照条件概率的定义,有如下离散随机变量的条件分布列:定义$P(Y = y_{j})=p_{·j}=\sum_{i = 1}^{n}p_{ij}$.对于固定的$j$,若$p_{·j}>0$,则称$p_{i|j}=P(X = x_{i}|Y = y_{j})=\frac{p_{ij}}{p_{·j}}(i = 1,2,\cdots,n)$为给定$Y = y_{j}$条件下的$X$条件分布列.
离散随机变量的条件分布的数学期望(若存在)定义如下:$E(X|Y = y)=\sum_{i = 1}^{n}x_{i}P(X = x_{i}|Y = y)$.
(Ⅰ)设二维离散随机变量$(X,Y)$的联合分布列为

求给定$X = 1$条件下的$Y$条件分布列;
(Ⅱ)设$(X,Y)$为二维离散随机变量,且$E(X)$存在,证明:$E(X)=\sum_{j = 1}^{m}E(X|Y = y_{j})\cdot p_{·j}$;
(Ⅲ)某人被困在有三个门的迷宫里,第一个门通向离开迷宫的道,沿此道走30分钟可走出迷宫;第二个门通一条迷道,沿此迷道走50分钟又回到原处;第三个门通一条迷道,沿此迷道走70分钟也回到原处,假定此人总是等可能地在三个门中选择一个,试求他平均要用多少时间才能走出迷宫.
答案:
离散型随机变量的分布列与数学期望 解:(Ⅰ)因为$P(X = 1) = p_{1\cdot} = 0.6$,所以用第一行各元素分别除以 0.6,可得给定$X = 1$条件下的$Y$条件分布列: | $Y|X = 1$ | 1 | 2 | 3 | | --- | --- | --- | --- | | $P$ | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{1}{3}$ | (5 分) (Ⅱ)证明:二维离散随机变量$(X,Y)$的概率为$P(X = x_i,Y = y_j) = p_{ij}(i = 1,2,\cdots,n,j = 1,2,\cdots,m)$,由$p_{ij} = p_{i|j}\cdot p_{\cdot j}$,得$E(X) = \sum_{i = 1}^{n}x_i\cdot p_{i\cdot} = \sum_{i = 1}^{n}x_i\cdot(\sum_{j = 1}^{m}p_{ij}) = \sum_{i = 1}^{n}\sum_{j = 1}^{m}(x_i\cdot p_{ij}) = \sum_{j = 1}^{m}\sum_{i = 1}^{n}(x_i\cdot p_{ij})$(题眼),(7 分)则$E(X) = \sum_{j = 1}^{m}(\sum_{i = 1}^{n}x_i\cdot p_{i|j}\cdot p_{\cdot j}) = \sum_{j = 1}^{m}(\sum_{i = 1}^{n}x_ip_{i|j})\cdot p_{\cdot j}$(关键:由题中所给定义得出$E(X)$的表达式是解题关键). (9 分)由$\sum_{i = 1}^{n}x_ip_{i|j} = E(X|Y = y_j)$,有$E(X) = \sum_{j = 1}^{m}E(X|Y = y_j)\cdot p_{\cdot j}$. (11 分) (Ⅲ)由(Ⅱ)知,对于二维离散随机变量$(X,Y)$,$E(X) = \sum_{j = 1}^{m}E(X|Y = y_j)\cdot P(Y = y_j)$. 设他需要$X$分钟离开迷宫,记$Y$表示第一次所选的门,事件$\{Y = i\}$表示选第$i$个门(题眼),由题设有$P(Y = 1) = P(Y = 2) = P(Y = 3) = \frac{1}{3}$. (12 分)因为选第一个门后 30 分钟可离开迷宫,所以$E(X|Y = 1) = 30$. (13 分)又因为选第二个门后 50 分钟回到原处,所以$E(X|Y = 2) = 50 + E(X)$. (14 分)又因为选第三个门后 70 分钟也回到原处,所以$E(X|Y = 3) = 70 + E(X)$,(15 分)所以$E(X) = \frac{1}{3}\times(30 + 50 + E(X) + 70 + E(X)) = 50 + \frac{2}{3}E(X)$(提示:离散型随机变量的数学期望),(16 分)解得$E(X) = 150$. 即他平均要用 150 分钟才能走出迷宫. (17 分)
查看更多完整答案,请扫码查看


