《2025年一遍过九年级数学下册冀教版》

10 若线段CD是线段AB的正投影，则AB与CD的大小关系为（ ）
A. AB ＞ CD
B. AB ＜ CD
C. AB = CD
D. AB≥CD

答案： D@@若线段AB平行于投影面，则AB = CD，若线段AB不平行于投影面，则AB ＞ CD。综上，可得AB≥CD。

11 [2024保定竞秀区期末]下列说法正确的是（ ）
A. 物体在阳光下的投影只与物体的高度有关
B. 小明的个子比小亮高，我们可以肯定，不论什么情况，小明的影子一定比小亮的影子长
C. 物体在阳光照射下，不同时刻，影长可能发生变化，方向也可能发生变化
D. 物体在阳光照射下，影子的长度和方向都是固定不变的

答案： C@@物体在阳光下的投影不只与物体的高度有关，还与阳光照射的角度有关，A项错误；小明的个子比小亮高，在不同的时间或不同的位置，小明的影子可能比小亮的影子短，B项错误；不同时刻物体在太阳光下的影子的长度可能会改变，方向可能会改变，C项正确，D项错误。

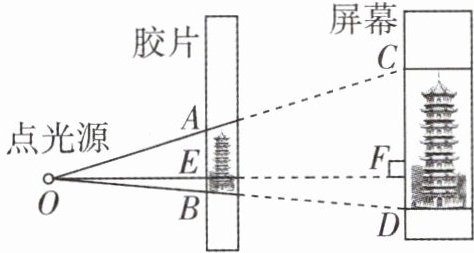
12 [跨学科·物理][2024温州模拟]如图，点光源O射出的光线沿直线传播，将胶片上的建筑物图片AB投影到与胶片平行的屏幕上，形成影像CD. 已知AB = 0.3 dm，点光源到胶片的距离OE长为6 dm，CD长为4.3 dm，则胶片与屏幕的距离EF为（ ）

A. 86 dm
B. 84 dm
C. 80 dm
D. 78 dm

答案： C@@
∵AB//CD，
∴△OAB∽△OCD（平行于三角形一边的直线与其他两边相交，截得的三角形与原三角形相似），
∵OF⊥CD，
∴OF⊥AB，
∴$\frac{AB}{CD}=\frac{OE}{OF}$，
∴$\frac{0.3}{4.3}=\frac{6}{6 + EF}$，
∴EF = 80 dm。

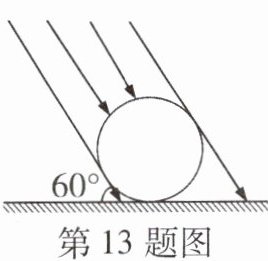
13 如图，太阳光线与水平地面成60°的角，照在地面的一个排球上，排球在地面的投影长是14√3 cm，则排球的直径是（ ）

A. 7 cm
B. 14 cm
C. 21 cm
D. 21√3 cm

答案：
C@@如图，易知AB为排球的直径，CD = AB，CE = 14$\sqrt{3}$ cm，∠CDE = 90°。在Rt△CDE中，sin∠CED =$\frac{CD}{CE}$，所以CD = 14$\sqrt{3}$sin 60° = 14$\sqrt{3}$×$\frac{\sqrt{3}}{2}$= 21（cm），所以排球的直径为21 cm。

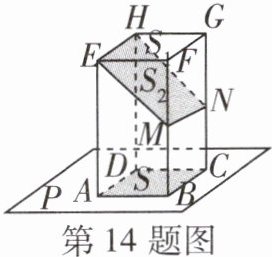
14 [教材P91“一起探究”T2变式]如图，长方体的一个底面ABCD在投影面P上，M，N分别是侧棱BF，CG的中点，矩形EFGH与矩形EMNH的正投影都是矩形ABCD，设矩形EFGH，EMNH，ABCD的面积分别是S₁，S₂，S，则S₁，S₂，S的关系是__________.（用“ = ”“ ＞ ”或“ ＜ ”连起来）

答案： $S_1 = S ＜ S_2$
∵长方体的底面ABCD//底面EFGH，且矩形EFGH的正投影是矩形ABCD，
∴$S_1 = S$。
∵EM ＞ EF，EH = EH，
∴$S_1 ＜ S_2$，
∴$S_1 = S ＜ S_2$。

15 [2023衡水月考]如图，身高1.6米的小明从距路灯的底部（点O）20米的点A处沿AO方向行走14米到点C处，小明在A处，头顶B在路灯投影下形成的影子在M处.

(1)已知灯杆垂直于路面，试标出路灯P的位置和小明在C处，头顶D在路灯投影下形成的影子N的位置.
(2)若路灯（点P）距地面8米，小明从A到C时，身影的长度是变长了还是变短了？变长或变短了多少米？

答案：
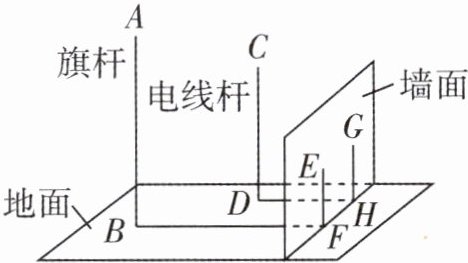
解：（1）点P和点N的位置如图所示。!（2）设在A处时影长AM为x米，在C处时影长CN为y米， 由$\frac{x}{x + 20}=\frac{1.6}{8}$，解得x = 5， 由$\frac{y}{y + 6}=\frac{1.6}{8}$，解得y = 1.5， x - y = 5 - 1.5 = 3.5。 答：变短了，变短了3.5米。

16 [几何直观][2024毕节期末]如图，在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD，它们都与地面垂直. 为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光照射下，旗杆落在围墙上的影子EF的长度为2米，落在地面上的影子BF的长度为10米，而电线杆落在围墙上的影子GH的长度为3米，落在地面上的影子DH的长度为5米. 依据这些数据，该小组的同学计算出了电线杆的高度.
(1)该小组的同学在这里利用的是__________投影的有关知识进行计算的；
(2)试计算出电线杆的高度，并写出计算的过程.

答案：
解：（1）平行 （2）如图，过点E作EM⊥AB于点M，过点G作GN⊥CD于点N，连接AE，CG。!则MB = EF = 2米，ND = GH = 3米，ME = BF = 10米，NG = DH = 5米， 所以AM = 10 - 2 = 8（米）。 由平行投影的性质，可知$\frac{AM}{ME}=\frac{CN}{NG}$，即$\frac{8}{10}=\frac{CD - 3}{5}$， 所以CD = 7米，即电线杆的高度为7米。 归纳总结 测量实物的高度、宽度时，关键是要构造和实物所在三角形相似的三角形，而且要能测量已知三角形的各边的长，运用相似三角形的性质列出比例式求解。