《2025年一遍过九年级数学下册冀教版》

1 [2024 保定安新实验中学期末]某商家通过“直播带货”使商品的网上零售额得以迅速增长. 若该商家销售一种进价为每件 10 元的日用商品，经调查发现，该商品每天的销售量$y$(件)与销售单价$x$(元)满足$y = - 10x + 400$，设销售这种商品每天的利润为$W$(元). 若每天至少销售 60 件，且销售单价不低于 30 元，则$W$的最大值是 ( )
A. 4 000
B. 2 500
C. 2 250
D. 2 000

答案： 由题意，得$\begin{cases}-10x + 400\geq60 \\ x\geq30\end{cases}$，解得$30\leq x\leq34$，$W=(x - 10)y=(x - 10)( - 10x + 400)= - 10x^{2}+500x - 4000=-10(x - 25)^{2}+2250$。$\because - 10\lt0$，$\therefore$当$x\gt25$时，$W$随$x$的增大而减小，$\therefore$当$x = 30$时，$W$有最大值，最大值为$-10\times(30 - 25)^{2}+2250 = 2000$。 #### 易错分析 求实际问题中的最值时，注意自变量的取值范围，本题中，由于题目的限制条件，$W$的最大值不能达到$2250$。

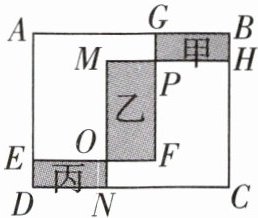
2 [2023 六安皋城中学二模]如图，学校准备在长为 16 m、宽为 12 m 的矩形草地上规划甲、乙、丙三个区域栽种花卉，正方形$AEFG$和正方形$CHMN$面积相等，且各有两边在长方形边上，矩形$MOFP$是这两个正方形的重叠部分，设$PM$为$x(2\leqslant x\leqslant4)$m，$PF$为$y$m.
(1)求$y$关于$x$的函数表达式；(不用写出自变量的取值范围)
(2)设甲、乙、丙的总面积为$S(m^{2})$，求$S$关于$x$的函数表达式及$S$的最大值.

答案： 解：
(1) 由题可知，$AG + MH = 16 + PM$，$AE + MN = 12 + PF$，$\therefore16 + PM = 12 + PF$（正方形$AEFG$和正方形$CHMN$边长相等），即$16 + x = 12 + y$，$\therefore y = x + 4$。
(2) $\because$正方形$AEFG$和正方形$CHMN$的面积相等，$\therefore AG = MH$，$\therefore2AG = 16 + x$，$\therefore S_{正方形AEFG}=S_{正方形CHMN}=(\frac{16 + x}{2})^{2}$，又$\because S_{乙}=(x + 4)x$，$\therefore S = S_{甲}+S_{乙}+S_{丙}=16\times12-(S_{正方形AEFG}+S_{正方形CHMN}-2S_{乙})=16\times12 - 2(\frac{16 + x}{2})^{2}+2(x + 4)x$，整理得$S=\frac{3}{2}x^{2}-8x + 64=\frac{3}{2}(x - \frac{8}{3})^{2}+64-\frac{32}{3}$，$\because\frac{3}{2}\gt0$，故当$x\gt\frac{8}{3}$时，$S$随$x$的增大而增大，当$x\lt\frac{8}{3}$时，$S$随$x$的增大而减小，又$\because|4-\frac{8}{3}|\gt|12-\frac{8}{3}|$，$\therefore$当$x = 4$时，$S$取最大值，$S_{最大}=\frac{3}{2}\times4^{2}-8\times4 + 64 = 56$。

3 已知关于$x$的函数$y = (m + 6)x^{2} + 2(m - 1)x + m + 1$的图像与$x$轴有交点，则实数$m$的取值范围为_______.

答案： $m\leq-\frac{5}{9}$ ①当$m + 6 = 0$，即$m = - 6$时，函数$y=(m + 6)x^{2}+2(m - 1)x + m + 1=-14x - 5$的图像与$x$轴有一个交点。 ②当$m + 6\neq0$时，一元二次方程$(m + 6)x^{2}+2(m - 1)x + m + 1 = 0$的根的判别式$b^{2}-4ac = 4(m - 1)^{2}-4(m + 6)(m + 1)= - 36m - 20\geq0$，解得$m\leq-\frac{5}{9}$，所以当$m\leq-\frac{5}{9}$且$m\neq - 6$时，抛物线与$x$轴有交点。综上所述，当$m\leq-\frac{5}{9}$时，关于$x$的函数$y=(m + 6)x^{2}+2(m - 1)x + m + 1$的图像与$x$轴有交点。 #### 易错分析 分析函数$y=(m + 6)x^{2}+2(m - 1)x + m + 1$的图像与$x$轴有交点时，应运用分类讨论思想，讨论函数分别为一次函数和二次函数的情况，当函数为一次函数时的条件是$m + 6 = 0$，当函数为二次函数时的条件是$m + 6\neq0$，且$b^{2}-4ac\geq0$。

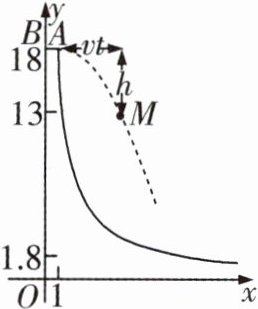
4 如图是轮滑场地的截面示意图，建立平面直角坐标系，且平台$AB$距$x$轴(水平)18 m，与$y$轴交于点$B$，与滑道$y = \frac{k}{x}(x\geqslant1)$交于点$A$，且$AB = 1$m. 运动员(看成点)在$BA$方向获得速度$v$ m/s 后，从$A$处向右下方飞向滑道，点$M$是下落路线上的某一位置. 忽略空气阻力，实验表明：$M$，$A$的竖直距离$h$(m)与飞出时间$t$(s)的平方成正比，且$t = 1$时，$h = 5$，点$M$，$A$的水平距离是$vt$ m.
(1)求$k$的值，并用$t$表示$h$；
(2)设$v = 5$，用$t$表示点$M$的横坐标$x$和纵坐标$y$，并求$y$与$x$之间的关系式(不写$x$的取值范围)，以及$y = 13$时，运动员与正下方滑道的竖直距离；
(3)若运动员甲、乙同时从$A$处飞出，速度分别是 5 m/s，$v_{乙}$ m/s，当甲距离$x$轴 1.8 m，且乙位于甲右侧超过 4.5 m 的位置时，直接写出$t$的值及$v_{乙}$的取值范围.

答案： 解：
(1) 根据题意，得点$A$的坐标为$(1,18)$，则$k = 1\times18 = 18$。设$h = mt^{2}$，当$t = 1$时，$h = 5$，解得$m = 5$，所以$h = 5t^{2}$。
(2) 根据题意，得$x = vt + 1$，当$v = 5$时，$x = 5t + 1$，① 由$y = 18 - h$，$h = 5t^{2}$，得$y = 18 - 5t^{2}$。② 由①，得$t=\frac{x - 1}{5}$，③ 将③代入②，得$y = 18 - 5t^{2}=18 - 5\times(\frac{x - 1}{5})^{2}$，化简，得$y = -\frac{1}{5}(x - 1)^{2}+18$。当$y = 13$时，即$-\frac{1}{5}(x - 1)^{2}+18 = 13$，解得$x_{1}=6$，$x_{2}=-4$（舍去），将$x = 6$代入$y=\frac{18}{x}$，得$y = 3$，$13 - 3 = 10(m)$，所以此时运动员与正下方滑道的竖直距离为$10m$。
(3)$t=\frac{9}{5}$，$v_{乙}$的取值范围为$v_{乙}\gt7.5$。根据题意，知当甲距离$x$轴$1.8m$时，$y = -\frac{1}{5}(x - 1)^{2}+18 = 1.8$，解得$x_{1}=10$，$x_{2}=-8$（舍去），当$x = 10$时，$t=\frac{10 - 1}{5}=\frac{9}{5}$。而此时$x_{乙}\gt10 + 4.5 = 14.5$，即$x_{乙}=v_{乙}t + 1\gt14.5$，整理，得$\frac{9}{5}v_{乙}+1\gt14.5$，解得$v_{乙}\gt7.5$。