《2025年一遍过九年级数学下册冀教版》

1 [教材 P40A 组 T2 变式]若一个二次函数的图像经过点$A(0,0)$,$B(-1,-11)$,$C(1,9)$,则这个二次函数的表达式是 ( )
A. $y=-10x^{2}+x$
B. $y=-10x^{2}+19x$
C. $y = 10x^{2}+x$
D. $y=-x^{2}+10x$

答案： D

2 已知抛物线$y = ax^{2}+bx + c$经过$A$,$B$,$C$三点,当$x\geqslant0$时,图像如图所示,则抛物线的顶点坐标为_______.

答案： $(\frac{3}{2},\frac{25}{8})$ 由题图可知 $A(0,2)$，$B(4,0)$，$C(5,-3)$，把 $A$，$B$，$C$ 三点的坐标分别代入抛物线的表达式 $y = ax^{2}+bx + c$，得 $\begin{cases}c = 2\\16a+4b + c = 0\\25a+5b + c=-3\end{cases}$，解得 $\begin{cases}a=-\frac{1}{2}\\b=\frac{3}{2}\\c = 2\end{cases}$，$\therefore$ 抛物线的表达式为 $y=-\frac{1}{2}x^{2}+\frac{3}{2}x + 2=-\frac{1}{2}(x-\frac{3}{2})^{2}+\frac{25}{8}$，$\therefore$ 抛物线的顶点坐标为 $(\frac{3}{2},\frac{25}{8})$。

3 [2024 邯郸旭日中学期中]已知顶点为$(2,4)$的抛物线过点$(4,0)$,此抛物线的表达式是 ( )
A. $y=-(x - 2)^{2}+4$
B. $y=(x - 2)^{2}-4$
C. $y=(x - 2)^{2}+4$
D. $y=-(x - 2)^{2}-4$

答案： A 由二次函数图像的顶点坐标是 $(2,4)$，可设这个二次函数的表达式为 $y = a(x - 2)^{2}+4(a\neq0)$，将 $(4,0)$ 代入，得 $4a+4 = 0$，解得 $a=-1$，$\therefore$ 这个二次函数的表达式为 $y=-(x - 2)^{2}+4$。

4 [2023 石家庄期末]二次函数的部分图像如图所示,图像的对称轴是直线$x=-1$,则这个二次函数的表达式为 ( )

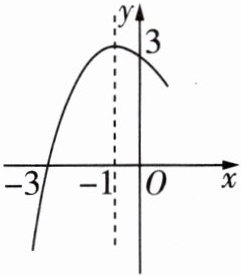
A. $y=-x^{2}+2x + 3$
B. $y=x^{2}+2x + 3$
C. $y=-x^{2}+2x - 3$
D. $y=-x^{2}-2x + 3$

答案： D 设这个二次函数的表达式为 $y = a(x + 1)^{2}+k(a\neq0)$，将 $(-3,0)$，$(0,3)$ 代入，得 $\begin{cases}4a + k = 0\\a + k = 3\end{cases}$，解得 $\begin{cases}a=-1\\k = 4\end{cases}$，则这个二次函数的表达式为 $y=-(x + 1)^{2}+4=-x^{2}-2x + 3$。

5 [2024 保定涿州实验中学月考]顶点为$(-5,-1)$,且开口方向,形状与函数$y=-\frac{1}{3}x^{2}$的图像相同的抛物线的表达式为____________.

答案： $y=-\frac{1}{3}(x + 5)^{2}-1$

6 二次函数的图像如图所示,则其表达式是 ( )

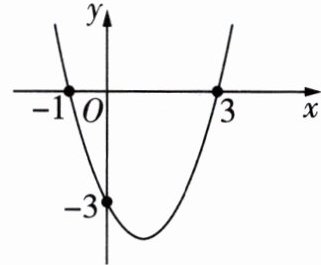
A. $y=-x^{2}+2x + 3$
B. $y=x^{2}-2x - 3$
C. $y=-x^{2}-2x + 3$
D. $y=-x^{2}-2x - 3$

答案： B 设抛物线的表达式为 $y = a(x + 1)(x - 3)$，将 $(0,-3)$ 代入，得 $a\times1\times(-3)=-3$，解得 $a = 1$，所以抛物线的表达式为 $y=(x + 1)(x - 3)$，即 $y=x^{2}-2x - 3$。

[变式 1][2024 天津外国语大学附属外国语学校月考]抛物线经过点$A(2,0)$,$B(-1,0)$,且与$y$轴交于点$C$. 若$OC = 2$,则该抛物线的表达式为________________.

答案： $y=-x^{2}+x + 2$ 或 $y=x^{2}-x - 2$ 抛物线与 $y$ 轴交于点 $C$，且 $OC = 2$，则点 $C$ 的坐标是 $(0,2)$ 或 $(0,-2)$，$\because$ 抛物线经过点 $A(2,0)$，$B(-1,0)$，可设该抛物线的表达式是 $y=a(x - 2)(x + 1)$，把 $(0,2)$ 代入表达式，得 $2=a(0 - 2)\times(0 + 1)$，解得 $a=-1$，则该抛物线的表达式是 $y=-(x - 2)(x + 1)$，即 $y=-x^{2}+x + 2$；同理可求得当点 $C$ 的坐标是 $(0,-2)$ 时，该抛物线的表达式是 $y=x^{2}-x - 2$。故该抛物线的表达式为 $y=-x^{2}+x + 2$ 或 $y=x^{2}-x - 2$。

[变式 2]已知二次函数的图像经过原点及点$(-\frac{1}{2},-\frac{1}{4})$,且图像与$x$轴的另一交点到原点的距离为 1,则该二次函数的表达式为________________.

答案： $y=-\frac{1}{3}x^{2}+\frac{1}{3}x$ 或 $y=x^{2}+x$ 当图像与 $x$ 轴的另一交点坐标为 $(1,0)$ 时，设二次函数的表达式为 $y = ax(x - 1)$，把 $(-\frac{1}{2},-\frac{1}{4})$ 代入，得 $-\frac{1}{4}=a(-\frac{1}{2})\times(-\frac{1}{2}-1)$，解得 $a=-\frac{1}{3}$，则二次函数的表达式为 $y=-\frac{1}{3}x^{2}+\frac{1}{3}x$；当图像与 $x$ 轴的另一交点坐标为 $(-1,0)$ 时，设二次函数的表达式为 $y = ax(x + 1)$，把 $(-\frac{1}{2},-\frac{1}{4})$ 代入，得 $-\frac{1}{4}=a(-\frac{1}{2})\times(-\frac{1}{2}+1)$，解得 $a = 1$，则二次函数的表达式为 $y=x^{2}+x$。故该二次函数的表达式为 $y=-\frac{1}{3}x^{2}+\frac{1}{3}x$ 或 $y=x^{2}+x$。

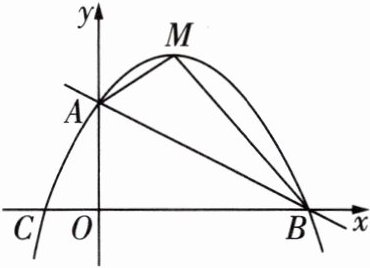
7 如图,在平面直角坐标系中,已知直线$y=-\frac{1}{2}x + 4$与$y$轴交于点$A$,与$x$轴交于点$B$,点$C$的坐标为$(-2,0)$.
(1)求经过$A$,$B$,$C$三点的抛物线的表达式；
(2)如果$M$为抛物线的顶点,连接$AM$,$BM$,求四边形$AOBM$的面积.

答案：
解：
(1) 在 $y=-\frac{1}{2}x + 4$ 中，令 $x = 0$，则 $y = 4$，令 $y = 0$，则 $x = 8$，$\therefore A(0,4)$，$B(8,0)$。设经过 $A$，$B$，$C$ 三点的抛物线的表达式为 $y = a(x + 2)(x - 8)$，将点 $A(0,4)$ 的坐标代入，得 $-16a = 4$，解得 $a=-\frac{1}{4}$，$\therefore y=-\frac{1}{4}(x + 2)(x - 8)=-\frac{1}{4}x^{2}+\frac{3}{2}x + 4$。
(2) $\because y=-\frac{1}{4}x^{2}+\frac{3}{2}x + 4=-\frac{1}{4}(x - 3)^{2}+\frac{25}{4}$，$\therefore M(3,\frac{25}{4})$。如图，过点 $M$ 作 $MD\perp x$ 轴于点 $D$，则 $MD=\frac{25}{4}$，$\therefore S_{四边形AOBM}=S_{梯形AODM}+S_{\triangle BDM}=\frac{1}{2}\times(4+\frac{25}{4})\times3+\frac{1}{2}\times5\times\frac{25}{4}=31$。 !（此处根据实际情况，若有图片编号可补充，文档中未明确给出图片编号，仅按格式示意）