第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1 [新考法 [2024 邯郸十三中模拟] 如图,将△ABC 折叠,使 AC 边落在 AB 边上,展开后得到折痕 AD,将△ABC 再次折叠,使 BC 边落在 BA 边上,展开后得到折痕 BE,BE,AD 交于点 O. 则下列结论一定成立的是 ( )

A. AO = 2OD
B. S_{△ABO}=S_{四边形 ODCE}
C. 点 O 到△ABC 三边的距离相等
D. 点 O 到△ABC 三个顶点的距离相等

A. AO = 2OD
B. S_{△ABO}=S_{四边形 ODCE}
C. 点 O 到△ABC 三边的距离相等
D. 点 O 到△ABC 三个顶点的距离相等
答案:
C@@如图,过点O作OF⊥AB于点F,OM⊥AC于点M,ON⊥BC于点N。由题意,得∠BAD = ∠CAD,∠ABE = ∠CBE,
∴ O为△ABC两内角平分线的交点,
∴ OF = OM = ON,
∴ 点O到△ABC三边的距离相等。
C@@如图,过点O作OF⊥AB于点F,OM⊥AC于点M,ON⊥BC于点N。由题意,得∠BAD = ∠CAD,∠ABE = ∠CBE,
∴ O为△ABC两内角平分线的交点,
∴ OF = OM = ON,
∴ 点O到△ABC三边的距离相等。

2 如图为 5×5 的网格图,A,B,C,D,O 均在格点上,则点 O 是 ( )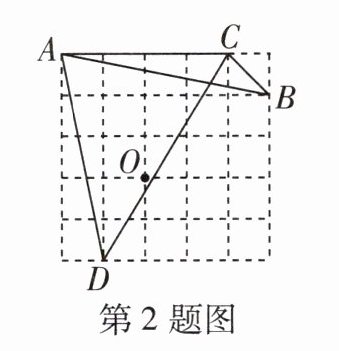
A. △ACD 的外心
B. △ABC 的外心
C. △ACD 的内心
D. △ABC 的内心

A. △ACD 的外心
B. △ABC 的外心
C. △ACD 的内心
D. △ABC 的内心
答案:
B@@连接OA,OB,OC,OD,设网格中小正方形的边长为1,则OA = OB = OC = √(3² + 2²) = √13,OD = √(2² + 1²) = √5,
∴ 点O是△ABC的外心。
∴ 点O是△ABC的外心。
3 [2023 北京四月月考] 根据尺规作图的痕迹,可用直尺成功找到三角形内心的是 ( )


答案:
C@@根据三角形内角和定理可知,第三个内角为65°,所以三角形是等腰三角形,再根据三角形的内心是内角平分线的交点,可得选项C能用直尺成功找到三角形内心。
4 如图,在△ABC 中,AB = AC,AI 平分∠BAC,O 是 AB 边上一点,以点 O 为圆心、OB 为半径的⊙O 切 AI 于点 I,交 AB 于 F,连接 BI.
(1)求证:I 是△ABC 的内心.
(2)连接 IF,若 IF = 2,求圆心 O 到 BI 的距离.
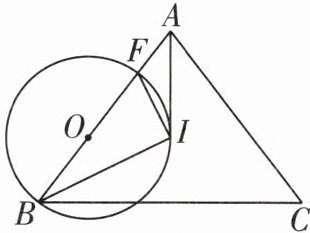
(1)求证:I 是△ABC 的内心.
(2)连接 IF,若 IF = 2,求圆心 O 到 BI 的距离.

答案:
(1)**证明**:如图,延长AI交BC于点D,连接OI,
∵ ⊙O切AI于点I,
∴ OI⊥AI。
∵ AB = AC,AI平分∠BAC,
∴ AD⊥BC,
∴ OI//BD,
∴ ∠1 = ∠2,
∵ OB = OI,
∴ ∠3 = ∠2,
∴ ∠1 = ∠3,即BI平分∠ABC。又
∵ AI平分∠BAC,
∴ I是△ABC的内心。(2)**解**:如图,过点O作OE⊥BI于点E,由垂径定理可知BE = IE。又
∵ OB = OF,
∴ OE是△FBI的中位线。
∵ IF = 2,
∴ OE = 1/2IF = 1,
∴ 圆心O到BI的距离是1。
(1)**证明**:如图,延长AI交BC于点D,连接OI,
∵ ⊙O切AI于点I,
∴ OI⊥AI。
∵ AB = AC,AI平分∠BAC,
∴ AD⊥BC,
∴ OI//BD,
∴ ∠1 = ∠2,
∵ OB = OI,
∴ ∠3 = ∠2,
∴ ∠1 = ∠3,即BI平分∠ABC。又
∵ AI平分∠BAC,
∴ I是△ABC的内心。(2)**解**:如图,过点O作OE⊥BI于点E,由垂径定理可知BE = IE。又
∵ OB = OF,
∴ OE是△FBI的中位线。
∵ IF = 2,
∴ OE = 1/2IF = 1,
∴ 圆心O到BI的距离是1。

5 [2024 北京大兴区期末] 如图,四边形 ABCD 内接于⊙O,点 I 是△ABC 的内心,∠AIC = 124°,点 E 在 AD 的延长线上,则∠CDE 的度数为 ( )

A. 56°
B. 62°
C. 68°
D. 78°

A. 56°
B. 62°
C. 68°
D. 78°
答案:
C@@因为点I是△ABC的内心,所以∠B = 2∠AIC - 180° = 68°,所以∠ADC = 112°,所以∠CDE的度数为68°。
6 [一题多解 [2023 衡水二模] 如图,在△ABC 中,∠ACB = 80°,AC = BC,M 是 AB 上一点(不与点 A 重合),点 P 是△ACM 的内心,则∠MPC 的度数 ( )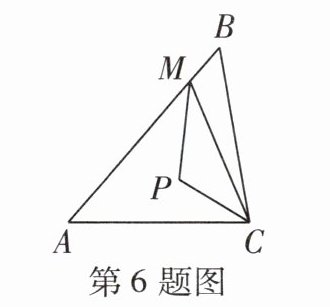
A. 等于 115°
B. 可以等于 80°
C. 等于 120°
D. 无法确定

A. 等于 115°
B. 可以等于 80°
C. 等于 120°
D. 无法确定
答案:
A@@- **通解**:
∵ ∠ACB = 80°,AC = BC,
∴ ∠B = ∠A = 50°。设∠BCM = x°,则∠MCA = 80° - x,∠AMC = 50° + x。
∵ 点P是△ACM的内心,
∴ CP平分∠MCA,MP平分∠AMC,
∴ ∠MCP = ∠ACP = 1/2∠MCA = 1/2(80° - x),∠CMP = ∠AMP = 1/2∠AMC = 1/2(50° + x),
∴ ∠MPC = 180° - ∠MCP - ∠CMP = 180° - 1/2(80° - x) - 1/2(50° + x°) = 115°。- **优解**:
∵ ∠ACB = 80°,AC = BC,
∴ ∠B = ∠A = 50°。
∵ 点P是△ACM的内心,
∴ ∠MPC = 90° + 1/2∠A = 115°。
∵ ∠ACB = 80°,AC = BC,
∴ ∠B = ∠A = 50°。设∠BCM = x°,则∠MCA = 80° - x,∠AMC = 50° + x。
∵ 点P是△ACM的内心,
∴ CP平分∠MCA,MP平分∠AMC,
∴ ∠MCP = ∠ACP = 1/2∠MCA = 1/2(80° - x),∠CMP = ∠AMP = 1/2∠AMC = 1/2(50° + x),
∴ ∠MPC = 180° - ∠MCP - ∠CMP = 180° - 1/2(80° - x) - 1/2(50° + x°) = 115°。- **优解**:
∵ ∠ACB = 80°,AC = BC,
∴ ∠B = ∠A = 50°。
∵ 点P是△ACM的内心,
∴ ∠MPC = 90° + 1/2∠A = 115°。
查看更多完整答案,请扫码查看


