第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
8 [2021河北中考]如图,⊙O的半径为6,将该圆周12等分后得到表盘模型,其中整钟点为An(n为1 ~ 12的整数),过点A7作⊙O的切线交A1A11的延长线于点P.
(1)通过计算比较直径和劣弧A7A11的长度哪个更长.
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系?请简要说明理由.
(3)求PA7的长度.

(1)通过计算比较直径和劣弧A7A11的长度哪个更长.
(2)连接A7A11,则A7A11和PA1有什么特殊位置关系?请简要说明理由.
(3)求PA7的长度.

答案:
(1)如图,连接$OA_{7}$,$OA_{11}$。 由圆周被$12$等分,得每份对应的圆心角是$30^{\circ}$, 所以劣弧$A_{7}A_{11}$所对圆心角$\angle A_{7}OA_{11}=120^{\circ}$, 所以劣弧$A_{7}A_{11}$的长$l=\frac{120\pi\times6}{180}=4\pi$。 因为$4\pi\gt12$,所以劣弧$A_{7}A_{11}$更长。@@
(2)$A_{7}A_{11}\perp PA_{1}$。 理由:如图,连接$OA_{1}$,则由$\overset{\frown}{A_{1}A_{7}}$等于圆周长的一半,可知$A_{1}$,$O$,$A_{7}$三点共线,则$A_{1}A_{7}$是$\odot O$的直径, 所以$\angle A_{7}A_{11}A_{1}=90^{\circ}$,所以$A_{7}A_{11}\perp PA_{1}$。@@
(3)因为$PA_{7}$是$\odot O$的切线,所以$\angle PA_{7}O = 90^{\circ}$, 由
(1)知$\angle A_{7}OA_{11}=120^{\circ}$, 又因为$OA_{11}=OA_{1}$, 所以$\angle A_{7}A_{1}A_{11}=60^{\circ}$,所以$\angle P = 30^{\circ}$, 所以$PA_{7}=\sqrt{3}A_{1}A_{7}=12\sqrt{3}$。
(1)如图,连接$OA_{7}$,$OA_{11}$。 由圆周被$12$等分,得每份对应的圆心角是$30^{\circ}$, 所以劣弧$A_{7}A_{11}$所对圆心角$\angle A_{7}OA_{11}=120^{\circ}$, 所以劣弧$A_{7}A_{11}$的长$l=\frac{120\pi\times6}{180}=4\pi$。 因为$4\pi\gt12$,所以劣弧$A_{7}A_{11}$更长。@@
(2)$A_{7}A_{11}\perp PA_{1}$。 理由:如图,连接$OA_{1}$,则由$\overset{\frown}{A_{1}A_{7}}$等于圆周长的一半,可知$A_{1}$,$O$,$A_{7}$三点共线,则$A_{1}A_{7}$是$\odot O$的直径, 所以$\angle A_{7}A_{11}A_{1}=90^{\circ}$,所以$A_{7}A_{11}\perp PA_{1}$。@@
(3)因为$PA_{7}$是$\odot O$的切线,所以$\angle PA_{7}O = 90^{\circ}$, 由
(1)知$\angle A_{7}OA_{11}=120^{\circ}$, 又因为$OA_{11}=OA_{1}$, 所以$\angle A_{7}A_{1}A_{11}=60^{\circ}$,所以$\angle P = 30^{\circ}$, 所以$PA_{7}=\sqrt{3}A_{1}A_{7}=12\sqrt{3}$。

9 [2024河北中考节选]已知⊙O的半径为3,弦MN = 2$\sqrt{5}$,△ABC中,∠ABC = 90°,AB = 3,BC = 3$\sqrt{2}$. 在平面上,先将△ABC和⊙O按图1位置摆放(点B与点N重合,点A在⊙O上,点C在⊙O内),随后移动△ABC,使点B在弦MN上移动,点A始终在⊙O上随之移动,设BN = x.
(1)当点B与点N重合时,求劣弧AN的长.
(2)当OA//MN时,如图2,求点B到OA的距离,并求此时x的值.
(3)设点O到BC的距离为d. 当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.
(1)当点B与点N重合时,求劣弧AN的长.
(2)当OA//MN时,如图2,求点B到OA的距离,并求此时x的值.
(3)设点O到BC的距离为d. 当点A在劣弧MN上,且过点A的切线与AC垂直时,求d的值.

答案:
(1)如图1,连接$OA$,$OB$。 由题意知$OA = OB = AB = 3$, 所以$\triangle AOB$为等边三角形,所以$\angle AOB = 60^{\circ}$, 所以劣弧$AN$的长为$\frac{60\pi\times3}{180}=\pi$。@@
(2)如图2,过点$B$作$BI\perp OA$于点$I$,过点$O$作$OH\perp MN$于点$H$,连接$ON$。 因为$OA// MN$,所以$\angle IBH=\angle AIB = 90^{\circ}$。 又因为$\angle BHO=\angle BIO = 90^{\circ}$, 所以四边形$BIOH$是矩形,所以$BH = OI$,$BI = OH$。 因为$MN = 2\sqrt{5}$,$OH\perp MN$,所以$MH = NH=\sqrt{5}$(垂径定理), 所以$OH=\sqrt{ON^{2}-NH^{2}} = 2$, 所以$BI = 2$,即点$B$到$OA$的距离为$2$。 在$Rt\triangle ABI$中,根据勾股定理,得$AI=\sqrt{AB^{2}-BI^{2}}=\sqrt{5}$, 所以$BH = OI = OA - AI = 3-\sqrt{5}$, 所以$x = BN = BH + NH = 3-\sqrt{5}+\sqrt{5}=3$。@@
(3)因为过点$A$的切线与$AC$垂直, 所以$AC$过圆心(此为关键点,可据此画出图形)。 如图3,过点$O$分别作$OJ\perp BC$于点$J$,$OK\perp AB$于点$K$(通过作辅助线,将求$OJ$的长转化为求$BK$的长)。 又因为$\angle ABC = 90^{\circ}$, 所以四边形$KOJB$是矩形, 所以$OJ = KB$。 因为$AB = 3$,$BC = 3\sqrt{2}$, 所以$AC=\sqrt{AB^{2}+BC^{2}} = 3\sqrt{3}$, 所以$\cos\angle BAC=\frac{AB}{AC}=\frac{3}{3\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{AK}{AO}$, 所以$AK=\sqrt{3}$, 所以$OJ = BK = 3-\sqrt{3}$,即$d = 3-\sqrt{3}$。

(1)如图1,连接$OA$,$OB$。 由题意知$OA = OB = AB = 3$, 所以$\triangle AOB$为等边三角形,所以$\angle AOB = 60^{\circ}$, 所以劣弧$AN$的长为$\frac{60\pi\times3}{180}=\pi$。@@
(2)如图2,过点$B$作$BI\perp OA$于点$I$,过点$O$作$OH\perp MN$于点$H$,连接$ON$。 因为$OA// MN$,所以$\angle IBH=\angle AIB = 90^{\circ}$。 又因为$\angle BHO=\angle BIO = 90^{\circ}$, 所以四边形$BIOH$是矩形,所以$BH = OI$,$BI = OH$。 因为$MN = 2\sqrt{5}$,$OH\perp MN$,所以$MH = NH=\sqrt{5}$(垂径定理), 所以$OH=\sqrt{ON^{2}-NH^{2}} = 2$, 所以$BI = 2$,即点$B$到$OA$的距离为$2$。 在$Rt\triangle ABI$中,根据勾股定理,得$AI=\sqrt{AB^{2}-BI^{2}}=\sqrt{5}$, 所以$BH = OI = OA - AI = 3-\sqrt{5}$, 所以$x = BN = BH + NH = 3-\sqrt{5}+\sqrt{5}=3$。@@
(3)因为过点$A$的切线与$AC$垂直, 所以$AC$过圆心(此为关键点,可据此画出图形)。 如图3,过点$O$分别作$OJ\perp BC$于点$J$,$OK\perp AB$于点$K$(通过作辅助线,将求$OJ$的长转化为求$BK$的长)。 又因为$\angle ABC = 90^{\circ}$, 所以四边形$KOJB$是矩形, 所以$OJ = KB$。 因为$AB = 3$,$BC = 3\sqrt{2}$, 所以$AC=\sqrt{AB^{2}+BC^{2}} = 3\sqrt{3}$, 所以$\cos\angle BAC=\frac{AB}{AC}=\frac{3}{3\sqrt{3}}=\frac{1}{\sqrt{3}}=\frac{AK}{AO}$, 所以$AK=\sqrt{3}$, 所以$OJ = BK = 3-\sqrt{3}$,即$d = 3-\sqrt{3}$。


根据以下素材,探索完成任务.
|背景素材|数学项目化课堂上,同学们用若干个大小不一的透明圆形(或半圆形)纸片,及一张宽2 cm且足够长的矩形纸带(如图1)设计了一系列任务,请帮助解决问题.
||
|----|----|----|
|任务一|若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过点A,B,G. 现测得AG = 1 cm,则可知该圆的半径为______cm.||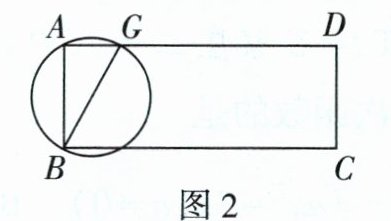
|任务二|同学乙将一张半圆形纸片与矩形纸带摆放成如图3所示,点A,E,F在半圆上. 若AE = 4 cm,BF = 5 cm,求圆的半径.||
|任务三|按图4摆放纸片,点A,P在圆上. 在AD边上取点M使AM = 2AB,作MN⊥BC于点N,连接AN恰好过圆心O,交圆于点Q,连接PN. 当直线PN与⊙O相切时,求⊙O的半径.||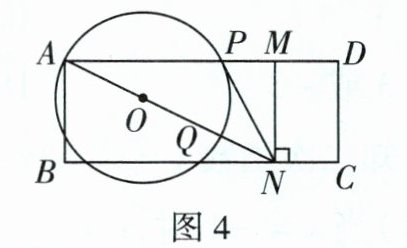
|背景素材|数学项目化课堂上,同学们用若干个大小不一的透明圆形(或半圆形)纸片,及一张宽2 cm且足够长的矩形纸带(如图1)设计了一系列任务,请帮助解决问题.

||
|----|----|----|
|任务一|若同学甲将一圆形纸片与矩形纸带摆放成如图2位置,使圆经过点A,B,G. 现测得AG = 1 cm,则可知该圆的半径为______cm.||

|任务二|同学乙将一张半圆形纸片与矩形纸带摆放成如图3所示,点A,E,F在半圆上. 若AE = 4 cm,BF = 5 cm,求圆的半径.||

|任务三|按图4摆放纸片,点A,P在圆上. 在AD边上取点M使AM = 2AB,作MN⊥BC于点N,连接AN恰好过圆心O,交圆于点Q,连接PN. 当直线PN与⊙O相切时,求⊙O的半径.||

答案:
本题可通过设圆的半径,利用垂径定理和勾股定理来求解。 设圆心为$O$,过点$O$作$OH\perp AB$于点$H$,连接$OA$。 因为$OH\perp AB$,根据垂径定理可知$H$为$AB$中点,又因为矩形纸带宽$2cm$,即$AB = 2cm$,所以$AH = \dfrac{1}{2}AB = 1cm$。 设圆的半径为$r cm$,已知$AG = 1cm$,则$OH = r - 1$。 在$Rt\triangle AOH$中,根据勾股定理$OA^{2}=AH^{2}+OH^{2}$,可得$r^{2}=1^{2}+(r - 1)^{2}$, 展开$(r - 1)^{2}$得$r^{2}=1 + r^{2}-2r + 1$, 移项可得$2r = 2$, 解得$r = 1$。 所以该圆的半径为$1cm$。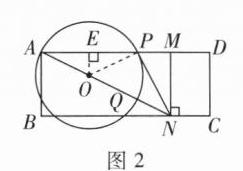
@@本题可通过作辅助线,构造直角三角形,利用勾股定理来求解圆的半径。 设半圆的圆心为$O$,半径为$r cm$,过点$O$作$OM\perp AE$于点$M$,作$ON\perp BF$于点$N$,连接$OA$,$OB$。 因为$OM\perp AE$,$ON\perp BF$,根据垂径定理可知$M$为$AE$中点,$N$为$BF$中点。 已知$AE = 4cm$,$BF = 5cm$,所以$AM = \dfrac{1}{2}AE = 2cm$,$BN = \dfrac{1}{2}BF = \dfrac{5}{2}cm$。 因为矩形纸带宽$2cm$,所以$OM = 2cm$,$ON = 2cm$。 在$Rt\triangle AOM$中,根据勾股定理$OA^{2}=AM^{2}+OM^{2}$,可得$r^{2}=2^{2}+2^{2}=8$。 在$Rt\triangle BON$中,根据勾股定理$OB^{2}=BN^{2}+ON^{2}$,可得$r^{2}=(\dfrac{5}{2})^{2}+2^{2}=\dfrac{25}{4}+4=\dfrac{41}{4}$。 由于$OA = OB = r$,所以$8=\dfrac{41}{4}$不成立,说明我们的思路存在问题。 重新考虑,设圆心为$O$,半径为$r$,过$O$作$OC\perp AB$于$C$,延长$CO$交$EF$于$D$。 因为$AB// EF$,所以$OD\perp EF$。 设$OC = x$,则$OD = r - x$。 在$Rt\triangle AOC$中,$AC^{2}=r^{2}-x^{2}$;在$Rt\triangle BOF$中,$BD^{2}=r^{2}-(r - x)^{2}$。 因为$AB = 2$,$AE = 4$,$BF = 5$,且$AC + BD = AB = 2$,$AE = 2\sqrt{r^{2}-x^{2}}$,$BF = 2\sqrt{r^{2}-(r - x)^{2}}$。 由$AE = 4$可得$\sqrt{r^{2}-x^{2}} = 2$,即$r^{2}-x^{2}=4$ ①; 由$BF = 5$可得$\sqrt{r^{2}-(r - x)^{2}}=\dfrac{5}{2}$,即$r^{2}-(r - x)^{2}=\dfrac{25}{4}$ ②。 由①得$x^{2}=r^{2}-4$,代入②可得: \[ \begin{aligned} r^{2}-(r^{2}-2rx + x^{2})&=\dfrac{25}{4}\\ r^{2}-r^{2}+2rx - x^{2}&=\dfrac{25}{4}\\ 2rx - (r^{2}-4)&=\dfrac{25}{4}\\ 2rx - r^{2}+4&=\dfrac{25}{4}\\ 2rx&=r^{2}+\dfrac{25}{4}-4\\ 2rx&=r^{2}+\dfrac{9}{4}\\ x&=\dfrac{r^{2}+\dfrac{9}{4}}{2r} \end{aligned} \] 将$x=\dfrac{r^{2}+\dfrac{9}{4}}{2r}$代入$x^{2}=r^{2}-4$可得: \[ \begin{aligned} (\dfrac{r^{2}+\dfrac{9}{4}}{2r})^{2}&=r^{2}-4\\ \dfrac{r^{4}+\dfrac{9}{2}r^{2}+\dfrac{81}{16}}{4r^{2}}&=r^{2}-4\\ r^{4}+\dfrac{9}{2}r^{2}+\dfrac{81}{16}&=4r^{4}-16r^{2}\\ 3r^{4}-\dfrac{41}{2}r^{2}-\dfrac{81}{16}&=0\\ 48r^{4}-328r^{2}-81&=0 \end{aligned} \] 设$r^{2}=t$,则$48t^{2}-328t - 81 = 0$, 对于一元二次方程$at^{2}+bt + c = 0(a\neq0)$,其求根公式为$t=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}$, 在$48t^{2}-328t - 81 = 0$中,$a = 48$,$b = -328$,$c = -81$, 则$t=\dfrac{328\pm\sqrt{(-328)^{2}-4\times48\times(-81)}}{2\times48}=\dfrac{328\pm\sqrt{107584 + 15552}}{96}=\dfrac{328\pm\sqrt{123136}}{96}=\dfrac{328\pm350.9}{96}$。 解得$t_{1}=\dfrac{328 + 350.9}{96}\approx7$,$t_{2}=\dfrac{328 - 350.9}{96}\lt0$(舍去)。 因为$r^{2}=t = 7$,所以$r=\sqrt{7}cm$。 所以圆的半径为$\sqrt{7}cm$。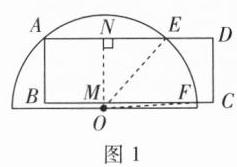
@@本题可通过设圆的半径,利用切线的性质和勾股定理来求解。 设圆的半径为$r$,$AB = a$,则$AM = 2a$。 因为$MN\perp BC$,四边形$ABCD$是矩形,所以四边形$ABNM$是矩形,则$BN = AM = 2a$,$MN = AB = a$。 连接$OP$,因为$PN$是$\odot O$的切线,所以$OP\perp PN$。 在$Rt\triangle ABN$中,根据勾股定理$AN^{2}=AB^{2}+BN^{2}=a^{2}+(2a)^{2}=5a^{2}$,则$AN=\sqrt{5}a$。 因为$AN$过圆心$O$,所以$AO = r$,$ON = AN - AO=\sqrt{5}a - r$。 在$Rt\triangle OPN$中,$OP = r$,$PN^{2}=BN^{2}+MN^{2}-BP^{2}=4a^{2}+a^{2}-(2r)^{2}=5a^{2}-4r^{2}$(设$BP = 2r$,因为$AN$过圆心,$P$在圆上)。 根据勾股定理$OP^{2}+PN^{2}=ON^{2}$,可得$r^{2}+5a^{2}-4r^{2}=(\sqrt{5}a - r)^{2}$, 展开$(\sqrt{5}a - r)^{2}$得$r^{2}+5a^{2}-4r^{2}=5a^{2}-2\sqrt{5}ar + r^{2}$, 移项可得$2r^{2}-2\sqrt{5}ar = 0$, 提取公因式$2r$得$2r(r - \sqrt{5}a)=0$, 则$r = 0$(舍去)或$r = \sqrt{5}a$。 所以$\odot O$的半径为$\sqrt{5}AB$。
本题可通过设圆的半径,利用垂径定理和勾股定理来求解。 设圆心为$O$,过点$O$作$OH\perp AB$于点$H$,连接$OA$。 因为$OH\perp AB$,根据垂径定理可知$H$为$AB$中点,又因为矩形纸带宽$2cm$,即$AB = 2cm$,所以$AH = \dfrac{1}{2}AB = 1cm$。 设圆的半径为$r cm$,已知$AG = 1cm$,则$OH = r - 1$。 在$Rt\triangle AOH$中,根据勾股定理$OA^{2}=AH^{2}+OH^{2}$,可得$r^{2}=1^{2}+(r - 1)^{2}$, 展开$(r - 1)^{2}$得$r^{2}=1 + r^{2}-2r + 1$, 移项可得$2r = 2$, 解得$r = 1$。 所以该圆的半径为$1cm$。

@@本题可通过作辅助线,构造直角三角形,利用勾股定理来求解圆的半径。 设半圆的圆心为$O$,半径为$r cm$,过点$O$作$OM\perp AE$于点$M$,作$ON\perp BF$于点$N$,连接$OA$,$OB$。 因为$OM\perp AE$,$ON\perp BF$,根据垂径定理可知$M$为$AE$中点,$N$为$BF$中点。 已知$AE = 4cm$,$BF = 5cm$,所以$AM = \dfrac{1}{2}AE = 2cm$,$BN = \dfrac{1}{2}BF = \dfrac{5}{2}cm$。 因为矩形纸带宽$2cm$,所以$OM = 2cm$,$ON = 2cm$。 在$Rt\triangle AOM$中,根据勾股定理$OA^{2}=AM^{2}+OM^{2}$,可得$r^{2}=2^{2}+2^{2}=8$。 在$Rt\triangle BON$中,根据勾股定理$OB^{2}=BN^{2}+ON^{2}$,可得$r^{2}=(\dfrac{5}{2})^{2}+2^{2}=\dfrac{25}{4}+4=\dfrac{41}{4}$。 由于$OA = OB = r$,所以$8=\dfrac{41}{4}$不成立,说明我们的思路存在问题。 重新考虑,设圆心为$O$,半径为$r$,过$O$作$OC\perp AB$于$C$,延长$CO$交$EF$于$D$。 因为$AB// EF$,所以$OD\perp EF$。 设$OC = x$,则$OD = r - x$。 在$Rt\triangle AOC$中,$AC^{2}=r^{2}-x^{2}$;在$Rt\triangle BOF$中,$BD^{2}=r^{2}-(r - x)^{2}$。 因为$AB = 2$,$AE = 4$,$BF = 5$,且$AC + BD = AB = 2$,$AE = 2\sqrt{r^{2}-x^{2}}$,$BF = 2\sqrt{r^{2}-(r - x)^{2}}$。 由$AE = 4$可得$\sqrt{r^{2}-x^{2}} = 2$,即$r^{2}-x^{2}=4$ ①; 由$BF = 5$可得$\sqrt{r^{2}-(r - x)^{2}}=\dfrac{5}{2}$,即$r^{2}-(r - x)^{2}=\dfrac{25}{4}$ ②。 由①得$x^{2}=r^{2}-4$,代入②可得: \[ \begin{aligned} r^{2}-(r^{2}-2rx + x^{2})&=\dfrac{25}{4}\\ r^{2}-r^{2}+2rx - x^{2}&=\dfrac{25}{4}\\ 2rx - (r^{2}-4)&=\dfrac{25}{4}\\ 2rx - r^{2}+4&=\dfrac{25}{4}\\ 2rx&=r^{2}+\dfrac{25}{4}-4\\ 2rx&=r^{2}+\dfrac{9}{4}\\ x&=\dfrac{r^{2}+\dfrac{9}{4}}{2r} \end{aligned} \] 将$x=\dfrac{r^{2}+\dfrac{9}{4}}{2r}$代入$x^{2}=r^{2}-4$可得: \[ \begin{aligned} (\dfrac{r^{2}+\dfrac{9}{4}}{2r})^{2}&=r^{2}-4\\ \dfrac{r^{4}+\dfrac{9}{2}r^{2}+\dfrac{81}{16}}{4r^{2}}&=r^{2}-4\\ r^{4}+\dfrac{9}{2}r^{2}+\dfrac{81}{16}&=4r^{4}-16r^{2}\\ 3r^{4}-\dfrac{41}{2}r^{2}-\dfrac{81}{16}&=0\\ 48r^{4}-328r^{2}-81&=0 \end{aligned} \] 设$r^{2}=t$,则$48t^{2}-328t - 81 = 0$, 对于一元二次方程$at^{2}+bt + c = 0(a\neq0)$,其求根公式为$t=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}$, 在$48t^{2}-328t - 81 = 0$中,$a = 48$,$b = -328$,$c = -81$, 则$t=\dfrac{328\pm\sqrt{(-328)^{2}-4\times48\times(-81)}}{2\times48}=\dfrac{328\pm\sqrt{107584 + 15552}}{96}=\dfrac{328\pm\sqrt{123136}}{96}=\dfrac{328\pm350.9}{96}$。 解得$t_{1}=\dfrac{328 + 350.9}{96}\approx7$,$t_{2}=\dfrac{328 - 350.9}{96}\lt0$(舍去)。 因为$r^{2}=t = 7$,所以$r=\sqrt{7}cm$。 所以圆的半径为$\sqrt{7}cm$。

@@本题可通过设圆的半径,利用切线的性质和勾股定理来求解。 设圆的半径为$r$,$AB = a$,则$AM = 2a$。 因为$MN\perp BC$,四边形$ABCD$是矩形,所以四边形$ABNM$是矩形,则$BN = AM = 2a$,$MN = AB = a$。 连接$OP$,因为$PN$是$\odot O$的切线,所以$OP\perp PN$。 在$Rt\triangle ABN$中,根据勾股定理$AN^{2}=AB^{2}+BN^{2}=a^{2}+(2a)^{2}=5a^{2}$,则$AN=\sqrt{5}a$。 因为$AN$过圆心$O$,所以$AO = r$,$ON = AN - AO=\sqrt{5}a - r$。 在$Rt\triangle OPN$中,$OP = r$,$PN^{2}=BN^{2}+MN^{2}-BP^{2}=4a^{2}+a^{2}-(2r)^{2}=5a^{2}-4r^{2}$(设$BP = 2r$,因为$AN$过圆心,$P$在圆上)。 根据勾股定理$OP^{2}+PN^{2}=ON^{2}$,可得$r^{2}+5a^{2}-4r^{2}=(\sqrt{5}a - r)^{2}$, 展开$(\sqrt{5}a - r)^{2}$得$r^{2}+5a^{2}-4r^{2}=5a^{2}-2\sqrt{5}ar + r^{2}$, 移项可得$2r^{2}-2\sqrt{5}ar = 0$, 提取公因式$2r$得$2r(r - \sqrt{5}a)=0$, 则$r = 0$(舍去)或$r = \sqrt{5}a$。 所以$\odot O$的半径为$\sqrt{5}AB$。
查看更多完整答案,请扫码查看


