第66页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
在4个完全相同的乒乓球上分别标上数字-1,0,1,3,然后装入一个不透明的口袋中摇匀.
(1)从口袋中随机摸出一个乒乓球,球上的数字是0是________事件.(填“必然”“随机”或“不可能”)
(2)从口袋中随机摸出一个乒乓球,球上的数字是正数的概率是________.
(3)一题多解 从口袋中随机摸出一个乒乓球,记下数字后放回摇匀,再从中随机摸出一个乒乓球,则两次摸球得到的数字之积为负数的概率是多少?
(4)从口袋中随机摸出一个乒乓球,记下数字后,不放回,再从中随机摸出一个乒乓球,则两次摸球得到的数字之积为非负数的概率是多少?
(5)嘉嘉和琪琪同时从口袋中各随机摸出一个乒乓球,若摸出的这两个乒乓球上的数字之和为偶数,则嘉嘉获胜,反之,琪琪获胜,这个游戏公平吗?为什么?
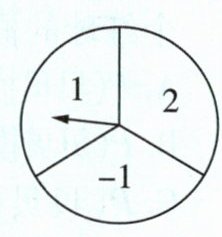
(6)如图,另有一个可以自由转动的转盘,被分成了面积相等的三个扇形,并在每个扇形内分别标上数字-1,1,2.转动转盘,将转盘指针指向的数字记作m(若指针指在分割线上,则重新转动转盘),再从口袋中随机摸出一个乒乓球,记下乒乓球上的数字n.
①求m,n相等的概率;
②求抛物线y = mx² + nx的对称轴在y轴左侧的概率.
(1)从口袋中随机摸出一个乒乓球,球上的数字是0是________事件.(填“必然”“随机”或“不可能”)
(2)从口袋中随机摸出一个乒乓球,球上的数字是正数的概率是________.
(3)一题多解 从口袋中随机摸出一个乒乓球,记下数字后放回摇匀,再从中随机摸出一个乒乓球,则两次摸球得到的数字之积为负数的概率是多少?
(4)从口袋中随机摸出一个乒乓球,记下数字后,不放回,再从中随机摸出一个乒乓球,则两次摸球得到的数字之积为非负数的概率是多少?
(5)嘉嘉和琪琪同时从口袋中各随机摸出一个乒乓球,若摸出的这两个乒乓球上的数字之和为偶数,则嘉嘉获胜,反之,琪琪获胜,这个游戏公平吗?为什么?
(6)如图,另有一个可以自由转动的转盘,被分成了面积相等的三个扇形,并在每个扇形内分别标上数字-1,1,2.转动转盘,将转盘指针指向的数字记作m(若指针指在分割线上,则重新转动转盘),再从口袋中随机摸出一个乒乓球,记下乒乓球上的数字n.
①求m,n相等的概率;
②求抛物线y = mx² + nx的对称轴在y轴左侧的概率.

答案:
(1)随机@@(2)$\frac{1}{2}$@@
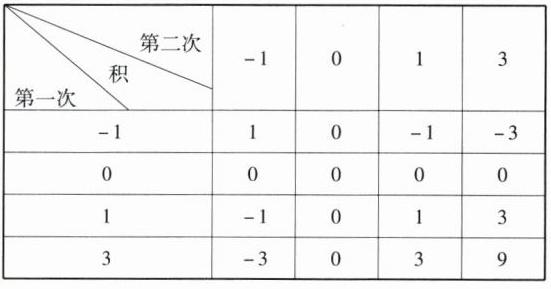
(3)
@@
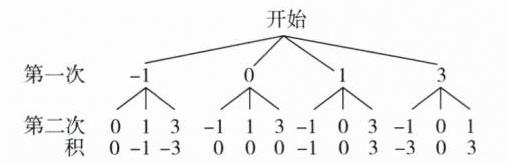
(4)
@@
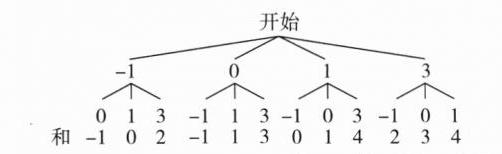
(5)


(1)随机@@(2)$\frac{1}{2}$@@
(3)

由表可知,共有16种等可能的结果,两次摸球得到的数字之
积为负数的结果有4种,所以两次摸球得到的数字之积为负
数的概率为
$\frac{4}{16}$=$\frac{1}{4}$@@
(4)

由树形图可知,共有12种等可能的结果,其中两次摸球得到
的数字之积为非负数的结果有8种,所以两次摸球得到的数
字之积为非负数的概率为
$\frac{8}{12}$=$\frac{2}{3}$@@
(5)

由树形图可知,共有12种等可能的结果,其中摸出的这两个
乒乓球上的数字之和为偶数的结果有6种(注意:0是偶数),
所以摸出的这两个乒乓球上的数字之和为偶数的概率为
$\frac{6}{12}$=$\frac{1}{2}$.故P(嘉嘉获胜)=
$\frac{1}{2}$.P(珙期获胜)=
$\frac{1}{2}$.所以这个游戏是公平的.
@@
(6)
(6)

由表可知,共有12种等可能的结果,其中 m,n相等的结果有
2种,
.m.n相等的概率为
$\frac{2}{12}$=$\frac{1}{6}$
由树形图可知
12种等可能的结果,其中抛物线y=
mux'+nx的对称轴在y轴左侧(即-
$\frac{n}{2m}$<0)的结果有5种,
所以抛物线y=mx+nx的对称轴在y轴左侧的概率为
$\frac{5}{12}$ 查看更多完整答案,请扫码查看


