第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
9 [新趋势·数学文化][2023长沙模拟]如图,八卦图是中国古老的科学文化遗产,是我国古代劳动人民智慧的结晶. 古人认为,世间万物皆可分类归至八卦之中. 八卦图中的每一卦由3根线组成. 如果从图中任选一卦,那么这一卦中恰有2根“——”和1根“--”的概率是 ( )

A. $\frac{1}{8}$
B. $\frac{1}{2}$
C. $\frac{3}{8}$
D. $\frac{5}{8}$

A. $\frac{1}{8}$
B. $\frac{1}{2}$
C. $\frac{3}{8}$
D. $\frac{5}{8}$
答案:
C
10 [教材P65T5变式][2024廊坊期末]一副不含大、小王的扑克牌共有52张,从中随机抽取1张,下列事件发生的概率最大的是 ( )
A. 抽到的牌是“K”
B. 抽到的牌是“红桃K”
C. 抽到的牌是“黑桃Q”
D. 抽到的牌是黑桃
A. 抽到的牌是“K”
B. 抽到的牌是“红桃K”
C. 抽到的牌是“黑桃Q”
D. 抽到的牌是黑桃
答案:
D
11 [跨学科·物理][2024深圳福田区模拟]李老师将6种生活现象制成如图所示看上去无差别的卡片,从中随机抽取一张卡片,卡片上的生活现象是物理变化的概率是 ( )

A. $\frac{1}{6}$
B. $\frac{2}{3}$
C. $\frac{1}{3}$
D. $\frac{1}{2}$

A. $\frac{1}{6}$
B. $\frac{2}{3}$
C. $\frac{1}{3}$
D. $\frac{1}{2}$
答案:
C
12 [2023重庆十一中期中]从 -2,-1,0,2,5中任取一个数记为a,则a的值使一元二次方程$2x^{2}-3x + a = 0$有实数根的概率为_______.
答案:
$\frac{3}{5}$
13 [教材P86T6变式][2023衡水检测]如图,将一个棱长为9 cm的大正方体分割成棱长为3 cm的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为_______.


答案:
$\frac{2}{9}$
14 一个不透明的布袋中有8个红球和16个白球,它们除颜色外都相同.
(1)求从袋中随机摸出一个球是红球的概率;
(2)现从袋中取走若干个白球,并放入相同数量的红球,搅拌均匀后,要使从袋中随机摸出一个球是红球的概率是$\frac{5}{8}$,求取走了多少个白球.
(1)求从袋中随机摸出一个球是红球的概率;
(2)现从袋中取走若干个白球,并放入相同数量的红球,搅拌均匀后,要使从袋中随机摸出一个球是红球的概率是$\frac{5}{8}$,求取走了多少个白球.
答案:
解:
(1) 布袋中有8个红球和16个白球,共24个球,故从袋中随机摸出一个球是红球的概率是$\frac{8}{24}=\frac{1}{3}$。
(2) 由题意,知球的总数不变,若随机摸出一个球是红球的概率是$\frac{5}{8}$,则红球的个数为$24\times\frac{5}{8}=15$,所以红球增加的个数为$15 - 8 = 7$,所以取走了7个白球。
(1) 布袋中有8个红球和16个白球,共24个球,故从袋中随机摸出一个球是红球的概率是$\frac{8}{24}=\frac{1}{3}$。
(2) 由题意,知球的总数不变,若随机摸出一个球是红球的概率是$\frac{5}{8}$,则红球的个数为$24\times\frac{5}{8}=15$,所以红球增加的个数为$15 - 8 = 7$,所以取走了7个白球。
15 [能力能力][2024宝鸡凤翔区期末]如图,一个转盘被平均分成12份,每份上面写上不同的数字,用这个转盘做游戏,规则规则:先猜数再转盘转盘,若指针指向的数字与所猜的数一致,则猜数者获胜,若指针在线在线上,则重转. 现提供三种猜数方法:
(1)猜“是奇数”或“是偶数”;
(2)猜“是大于10的数”或“大于大于10的数”;
(3)猜“是3的倍数”或“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?猜什么数?请说明理由.
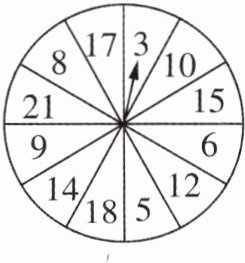
(1)猜“是奇数”或“是偶数”;
(2)猜“是大于10的数”或“大于大于10的数”;
(3)猜“是3的倍数”或“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?猜什么数?请说明理由.

答案:
解:选择第
(3)种猜数方法,猜“是3的倍数”。理由如下:因为转盘中,奇数与偶数的个数相同,大于10与不大于10的数的个数也相同,是3的倍数的数有7个,不是3的倍数的数有5个,所以选择第
(3)种猜数方法,猜“是3的倍数”获胜的机会大。
(3)种猜数方法,猜“是3的倍数”。理由如下:因为转盘中,奇数与偶数的个数相同,大于10与不大于10的数的个数也相同,是3的倍数的数有7个,不是3的倍数的数有5个,所以选择第
(3)种猜数方法,猜“是3的倍数”获胜的机会大。
查看更多完整答案,请扫码查看


