《2025年一遍过九年级数学下册冀教版》

13 [2023南充中考]若点$P(m,n)$在抛物线$y = ax^{2}(a\neq0)$上,则下列各点在抛物线$y = a(x + 1)^{2}$上的是 （ ）
A. $(m,n + 1)$
B. $(m + 1,n)$
C. $(m,n - 1)$
D. $(m - 1,n)$

答案： D

14 [2023廊坊广阳区期末]若二次函数$y = 2(x - 1)^{2}-1$的图像如图所示,则坐标原点可能是 （ ）

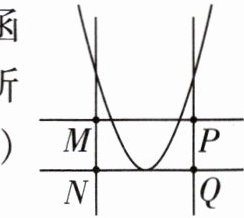
A. 点$M$
B. 点$N$
C. 点$P$
D. 点$Q$

答案： A

15 已知二次函数$y = -\frac{1}{2}(x - h)^{2}$,当自变量$x$的值满足当$1\leqslant x\leqslant 3$时,与其对应的函数值$y$的最大值为 -2,则常数$h$的值为 （ ）
A. 1或3
B. -1或1
C. 3或5
D. -1或5

答案： D

16 [新考法][2024石家庄裕华区外国语学校二模]已知$a ＞ 0$,设函数$y_{1} = a(x - 1)^{2},y_{2} = a(x - 2)^{2},y_{3} = a(x - 3)^{2}$. 直线$x = m$的图像与函数$y_{1},y_{2},y_{3}$的图像分别交于点$A(m,c_{1}),B(m,c_{2}),C(m,c_{3})$,下列说法正确的是 （ ）
A. 若$m ＜ 1$,则$c_{2} ＜ c_{3} ＜ c_{1}$
B. 若$1 ＜ m ＜ 2$,则$c_{1} ＜ c_{2} ＜ c_{3}$
C. 若$2 ＜ m ＜ 3$,则$c_{3} ＜ c_{2} ＜ c_{1}$
D. 若$m ＞ 3$,则$c_{3} ＜ c_{2} ＜ c_{1}$

答案：
D

17 [新趋势·结论开放][2023厦门五中期中]已知抛物线$y = a(x - 2)^{2}+1$与$x$轴有两个交点,把该抛物线向下平移$m$个单位长度得到新抛物线,新抛物线与$x$轴没有交点,则$m$的值可以是_______. (只填一个符合题意的值即可)

答案： 2

18 [2023南通十校月考]若二次函数$y = (x - m)^{2}-1$,当$x\leqslant 1$时,$y$随$x$的增大而减小,则$m$的取值范围是_______.

答案： m⩾1

19 [2023长春期末]如图,在平面直角坐标系中,抛物线$y = -\frac{2}{3}(x - 3)^{2}+k$经过坐标原点$O$,与$x$轴的另一个交点为$A$,过抛物线的顶点$B$分别作$BC\perp x$轴于点$C$,$BD\perp y$轴于点$D$,则图中阴影部分的面积和为_______.

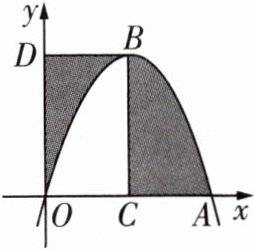
答案： 18

20 [2023石家庄四十七中质检]如图,在平面直角坐标系中,$O$为坐标原点,二次函数的图像$L:y = (x - h)^{2}-1(h$为常数)与$y$轴的公共点为$C$. 已知点$A( -4,1),B(0,1),P( -2, -1)$.
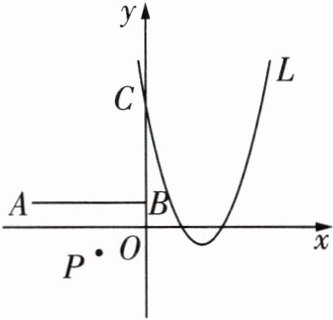
(1)当$L$经过点$P$时,该二次函数的表达式为_______,此时图像$L$的顶点坐标为_______;
(2)设点$C$的纵坐标为$y_{c}$,求$y_{c}$的最小值,当$y_{c}$取最小值时,图像$L$上有两点$(x_{1},y_{1}),(x_{2},y_{2})$,若$x_{1} ＜ x_{2}\leqslant0$,比较$y_{1}$与$y_{2}$的大小;
(3)当线段$AB$被$L$只分为两部分,且这两部分的比是1:3时,求$h$的值.

答案：

 解:
(1)y=(x+2)²-1 （-2,-1)

把点P（-2,-1)的坐标代人y=（x-h)²-1中，得-1=

（-2-h)²-1,解得h＝-2,.二次函数的表达式为y=

(x+2)²-1,此时图像L的顶点坐标为（ -2,-1).

@@
(2)令x=0,则y=(0-h)²-1=²-1,

= y. = h²-1,..当h =0时，y.。最小，最小值为- 1，

此时二次函数的表达式为y＝x²—1，

二次函数的图像开口向上，对称轴为y轴，

.当x<0时，y随×的增大而减小.

" 点(x,x)，(x,x)在二次函数的图像上，且x|<x;<0，

こy>Y・

@@（3): A(-4,1),B(0,1),

二L把AB分为1:3的两部分的点为（-3,1）或（-1,1)，

把(-3,1)代人y=（x-h)²-1中,得（ -3-h)²-1 =1,

解得h=-3-、/2或h=-3+、/2（舍去)（此时/与线段AB有

两个公共点，即线段AB被L分为三部分，下同）；

把（-1,1)代人y=（x-h)² -1中,得（-1 -h)² -1 =1,

解得h= -1+/2或h= -1-/2（舍去).

综上所述，h 的值为-3-2或-1 +、/2.

21 [抽象能力][2024石家庄外国语教育集团模拟]如图,点$A,B$的坐标分别为(1,4)和(4,4),抛物线$y = a(x - m)^{2}+n$的顶点在线段$AB$上运动,与$x$轴交于$C,D$两点(点$C$在点$D$的左侧).
(1)$n = $_______;
(2)若点$C$的横坐标的最小值为 -3,则点$D$的横坐标的最大值为_______.

答案：
(1)4@@
(2)8