第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1 [2024石家庄长安区一模]如图,已知P是⊙O外一点,用直尺和圆规过点P作一条直线,使它与⊙O相切于点M. 下面是琪琪给出的两种作法.
作法Ⅰ:如图1,作线段OP的垂直平分线交OP于点G;以点G为圆心,GP的长为半径画弧交⊙O于点M,作直线PM. 直线PM即为所求.
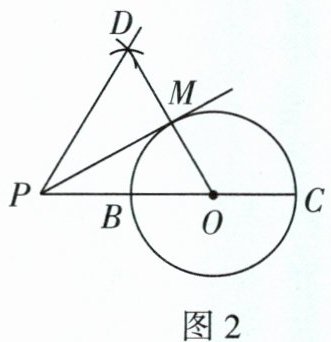
作法Ⅱ:如图2,连接OP,交⊙O于点B,作直径BC,以O为圆心,BC的长为半径作弧;以P为圆心,OP的长为半径作弧,两弧相交于点D,连接OD,交⊙O于点M,作直线PM. 直线PM即为所求.
对于琪琪的两种作法,下列说法正确的是( )

A. 两种作法都正确
B. 两种作法都错误
C. 作法Ⅰ正确,作法Ⅱ错误
D. 作法Ⅱ正确,作法Ⅰ错误
作法Ⅰ:如图1,作线段OP的垂直平分线交OP于点G;以点G为圆心,GP的长为半径画弧交⊙O于点M,作直线PM. 直线PM即为所求.
作法Ⅱ:如图2,连接OP,交⊙O于点B,作直径BC,以O为圆心,BC的长为半径作弧;以P为圆心,OP的长为半径作弧,两弧相交于点D,连接OD,交⊙O于点M,作直线PM. 直线PM即为所求.
对于琪琪的两种作法,下列说法正确的是( )


A. 两种作法都正确
B. 两种作法都错误
C. 作法Ⅰ正确,作法Ⅱ错误
D. 作法Ⅱ正确,作法Ⅰ错误
答案:
A
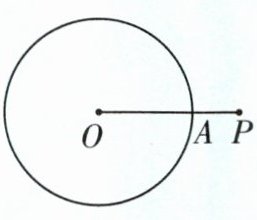
2 [2024廊坊十六中月考]如图,P是⊙O外一点,OP交⊙O于点A,OA = 2AP. 甲、乙两人想作一条过点P与⊙O相切的直线,其作法如下.
甲:以点A为圆心,AP的长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:取线段OP的中点M,以点M为圆心,OM的长为半径画弧,交⊙O于点B,则直线PB即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A. 甲正确,乙错误
B. 甲错误,乙正确
C. 两人都正确
D. 两人都错误
甲:以点A为圆心,AP的长为半径画弧,交⊙O于点B,则直线BP即为所求.
乙:取线段OP的中点M,以点M为圆心,OM的长为半径画弧,交⊙O于点B,则直线PB即为所求.
对于甲、乙两人的作法,下列判断正确的是( )

A. 甲正确,乙错误
B. 甲错误,乙正确
C. 两人都正确
D. 两人都错误
答案:
B
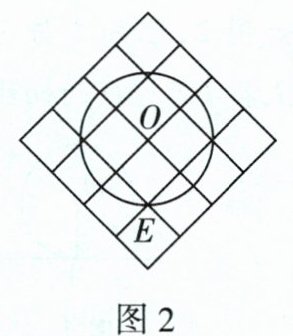
3 [2024吉林中考]图1、图2均是4×4的正方形网格,每个小正方形的顶点称为格点. 点A,B,C,D,E,O均在格点上. 图1中已画出四边形ABCD,图2中已画出以OE的长为半径的⊙O. 只用无刻度的直尺,在给定的网格中按要求画图.
(1)在图1中,画出四边形ABCD的一条对称轴;
(2)在图2中,画出经过点E的⊙O的切线.

(1)在图1中,画出四边形ABCD的一条对称轴;
(2)在图2中,画出经过点E的⊙O的切线.


答案:
- (1)(画法不唯一)如图1,取格点E,F,作直线EF,则直线EF即为所求。易证明四边形ABCD是矩形,且E,F分别为AB,CD的中点。 - (2)如图2,取格点G,H,作直线GH,则直线GH即为所求。易证明四边形OGTH是正方形,点E为正方形OGTH的中心,则OE⊥GH。
- (1)(画法不唯一)如图1,取格点E,F,作直线EF,则直线EF即为所求。易证明四边形ABCD是矩形,且E,F分别为AB,CD的中点。 - (2)如图2,取格点G,H,作直线GH,则直线GH即为所求。易证明四边形OGTH是正方形,点E为正方形OGTH的中心,则OE⊥GH。

4 用直尺和圆规作图,保留作图痕迹,不写作法:
(1)在图1中,已知⊙O₁,点P在⊙O₁上,过点P作⊙O₁的切线l₁;
(2)在图2中,已知⊙O₂,点Q在⊙O₂外,过点Q作⊙O₂的切线l₂.
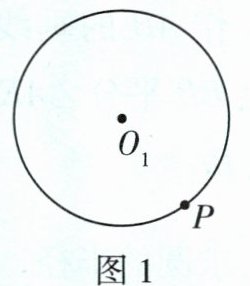
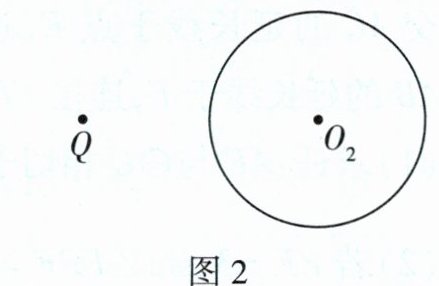
(1)在图1中,已知⊙O₁,点P在⊙O₁上,过点P作⊙O₁的切线l₁;
(2)在图2中,已知⊙O₂,点Q在⊙O₂外,过点Q作⊙O₂的切线l₂.


答案:
- (1)如图1,切线l₁为所作。 - (2)如图2,切线l₂(l₂')为所作。!
- (1)如图1,切线l₁为所作。 - (2)如图2,切线l₂(l₂')为所作。!

5 如图是由小正方形组成的9×7网格,每个小正方形的顶点叫做格点,A,B,C三个格点都在圆上,仅用无刻度的直尺在给定网格中完成画图.
(1)画出该圆的圆心O;
(2)画出格点E,连接EA,使EA为⊙O的一条切线,并画出过点E的另一条切线EF,切点为F.
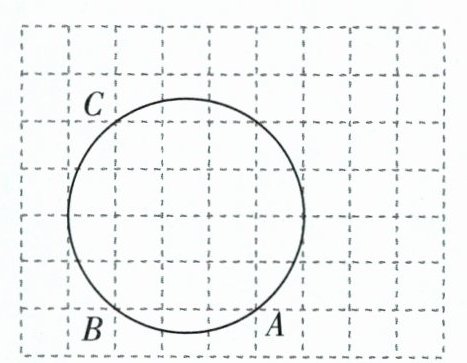
(1)画出该圆的圆心O;
(2)画出格点E,连接EA,使EA为⊙O的一条切线,并画出过点E的另一条切线EF,切点为F.

答案:
- (1)如图1,点O即为所求。 - (2)如图2,直线AE,EF即为所求。解法提示:由图2易知△CBA≌△AHE(SAS),所以∠CAB = ∠AEH。因为∠EAH + ∠AEH = 90°,所以∠EAH + ∠CAB = 90°,所以∠CAE = 90°,即OA⊥AE,所以EA为⊙O的一条切线。取格点P,Q,连接PQ,交网格线于点J,连接AJ交⊙O于点F,易得OE⊥AJ,进而可知点F与点A关于OE对称,则EF为⊙O的另一条切线。!
- (1)如图1,点O即为所求。 - (2)如图2,直线AE,EF即为所求。解法提示:由图2易知△CBA≌△AHE(SAS),所以∠CAB = ∠AEH。因为∠EAH + ∠AEH = 90°,所以∠EAH + ∠CAB = 90°,所以∠CAE = 90°,即OA⊥AE,所以EA为⊙O的一条切线。取格点P,Q,连接PQ,交网格线于点J,连接AJ交⊙O于点F,易得OE⊥AJ,进而可知点F与点A关于OE对称,则EF为⊙O的另一条切线。!

查看更多完整答案,请扫码查看


