第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1 [2023 石家庄二十八中期末]如图,已知 AB 为⊙O 的直径,CB 切⊙O 于点 B,CD 切⊙O 于点 D,交 BA 的延长线于点 E. 若 DE = 4,EB = 8,则△EBC 的面积为 ( )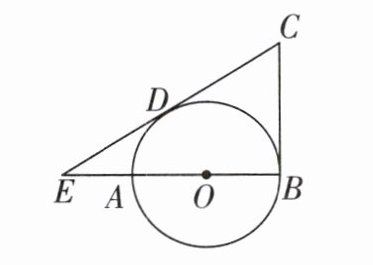
A. 24
B. 32
C. 36
D. 40

A. 24
B. 32
C. 36
D. 40
答案:
A
2 [2024 宁波七中期中]数轴上有 A,B 两点,点 B 表示实数 16,点 A 从原点出发,以每秒 2 个单位长度的速度向右运动,运动时间为 t,⊙B 的半径为 4. 若点 A 在⊙B 外,则 ( )
A. t < 6 或 t > 10
B. 6 < t < 10
C. t < 12 或 t > 20
D. 1 < t < 20
A. t < 6 或 t > 10
B. 6 < t < 10
C. t < 12 或 t > 20
D. 1 < t < 20
答案:
A
3 [2023 石家庄模拟]已知 PA,PB 是⊙O 的切线,A,B 是切点,点 C 是⊙O 上不同于点 A、点 B 的一个动点. 若∠P = 54°,则∠ACB 的度数是 ( )
A. 63°
B. 117°
C. 53°或 127°
D. 117°或 63°
A. 63°
B. 117°
C. 53°或 127°
D. 117°或 63°
答案:
D
4 [2023 承德期末]如图,在 Rt△ABC 中,∠C = 90°,AC = 5,BC = 12,⊙O 的半径为 3,当圆心 O 与点 C 重合时,⊙O 与直线 AB 的位置关系为________;若⊙O从点 C 开始沿直线 CA 移动,则当 OC = ________时,⊙O 与直线 AB 相切.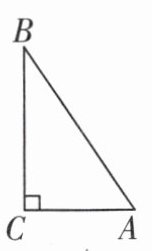

答案:
相离@@$\frac{7}{4}$或$\frac{33}{4}$
相离@@$\frac{7}{4}$或$\frac{33}{4}$

5 在平面直角坐标系中,以点(3,- 4)为圆心、r 为半径的圆与坐标轴有且只有 3 个公共点,则 r 的值是 ( )
A. 3
B. 4
C. 3 或 4
D. 4 或 5
A. 3
B. 4
C. 3 或 4
D. 4 或 5
答案:
D
D

6 [2024 重庆中考 B 卷]如图,AB 是⊙O 的直径,BC 是⊙O 的切线,点 B 为切点. 连接 AC 交⊙O 于点 D,点 E 是⊙O 上一点,连接 BE,DE,过点 A 作 AF//BE 交 BD 的延长线于点 F. 若 BC = 5,CD = 3,∠F = ∠ADE,则 AB 的长度是________;DF 的长度是________.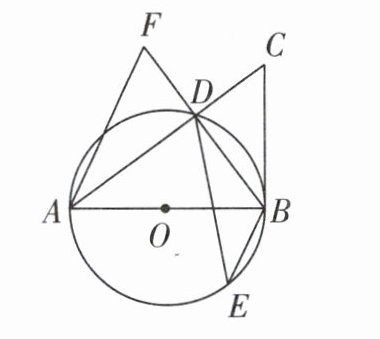

答案:
$\frac{20}{3}$@@$\frac{8}{3}$
$\frac{20}{3}$@@$\frac{8}{3}$

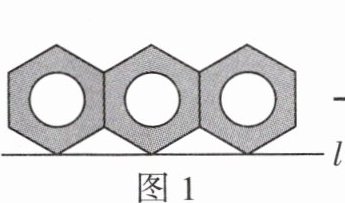
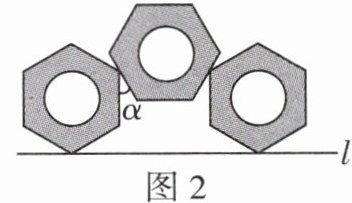
7 [新考法][2023 河北中考改编]将三个相同的六角形螺母并排摆放在桌面上,从上面看得到的平面图形如图 1,正六边形边长为 2 且各有一个顶点在直线 l 上,两侧螺母不动,把中间螺母抽出并重新摆放后,从上面看得到的平面图形如图 2,其中,中间的正六边形的一边与直线 l 平行,有两边分别经过两侧正六边形的一个顶点,则图 2 中:
(1)∠α = ________°;
(2)中间正六边形的中心到直线 l 的距离为________. (结果保留根号)
(1)∠α = ________°;
(2)中间正六边形的中心到直线 l 的距离为________. (结果保留根号)


答案:
30@@$2\sqrt{3}$
30@@$2\sqrt{3}$

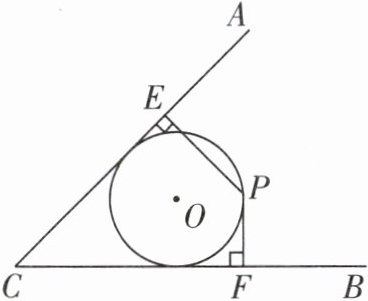
8 [2023 广元中考]如图,∠ACB = 45°,半径为 2 的⊙O 与角的两边相切,点 P 是⊙O 上任意一点,过点 P 向角的两边作垂线,垂足分别为 E,F,设t = PE + √2PF,则 t 的取值范围是________.

答案:
$2\sqrt{2}\leq t\leq4 + 2\sqrt{2}$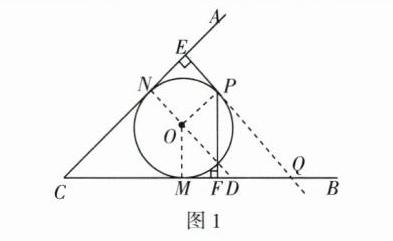

$2\sqrt{2}\leq t\leq4 + 2\sqrt{2}$


查看更多完整答案,请扫码查看


