第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
6 [教材P42T1变式][2023衡水模拟]某水利工程公司开挖的沟渠蓄水之后截面呈抛物线形,在图中建立平面直角坐标系,并标出相关数据(单位:m). 某学习小组探究之后得出下列结论,其中正确的为 ( )
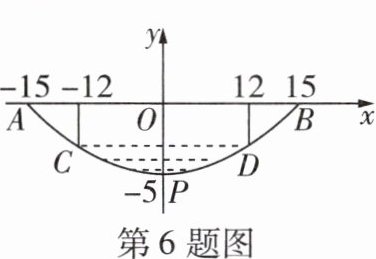
A. $AB = 24\ m$
B. 池底所在抛物线的表达式为$y = \frac{1}{25}x^{2} - 5$
C. 池塘水深最深处到水面$CD$的距离为3.2 m
D. 若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的$\frac{1}{3}$

A. $AB = 24\ m$
B. 池底所在抛物线的表达式为$y = \frac{1}{25}x^{2} - 5$
C. 池塘水深最深处到水面$CD$的距离为3.2 m
D. 若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的$\frac{1}{3}$
答案:
由题图可知$AB = 15 - (-15)=30(m)$,故选项A错误;设池底所在抛物线的表达式为$y = ax^{2}+bx + c$,将点$A(-15,0)$,$B(15,0)$,$P(0,-5)$的坐标分别代入抛物线的表达式中,得$\begin{cases}0 = (-15)^{2}a+(-15)b + c\\0 = 15^{2}a + 15b + c\\-5 = c\end{cases}$,解得$\begin{cases}a=\frac{1}{45}\\b = 0\\c = -5\end{cases}$,所以池底所在抛物线的表达式为$y = \frac{1}{45}x^{2}-5$,故选项B错误;池塘水深最深处为点$P(0,-5)$,$y_{C}=\frac{1}{45}\times(-12)^{2}-5 = -1.8$,所以池塘水深最深处到水面$CD$的距离为$-1.8 - (-5)=3.2(m)$,故选项C正确;若池塘中水面的宽度减少为原来的一半,将$x = 6$代入表达式,得$y = \frac{1}{45}\times6^{2}-5=\frac{4}{5}-5 = -\frac{21}{5}$,所以池塘水深最深处到水面的距离为$-\frac{21}{5}-(-5)=0.8(m)$,而原池塘水深最深处到水面的距离为$3.2m$,所以若池塘中水面的宽度减少为原来的一半,则最深处到水面的距离减少为原来的$\frac{1}{4}$,故选项D错误。
7 [新情境][2024长春三模]图1是一种神奇的鱼——射水鱼,当猎物进入视野后,它便会将头露出水面,合上鱼鳃,从嘴里射出抛物线形水柱,将猎物击落,已知水柱在离发射点水平距离为2 dm处达到最大高度9 dm. 现有一条射水鱼在水面的点$A$处,如图2,昆虫与点$A$的水平距离为2 dm,距离水面的高度为5 dm,射水鱼需要向右游动________dm才能击中昆虫.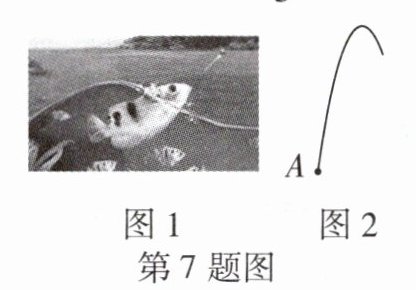

答案:
以点$A$为坐标原点,水面为$x$轴,竖直方向为$y$轴建立平面直角坐标系,设抛物线的函数表达式为$y = a(x - 2)^{2}+9$,将$(0,0)$代入,得$4a + 9 = 0$,解得$a = -\frac{9}{4}$。所以抛物线的函数表达式为$y = -\frac{9}{4}(x - 2)^{2}+9$,令$y = 5$,则$-\frac{9}{4}(x - 2)^{2}+9 = 5$,解得$x_{1}=\frac{10}{3}$(舍去),$x_{2}=\frac{2}{3}$,$2-\frac{2}{3}=\frac{4}{3}$。所以射水鱼需要向右游动$\frac{4}{3}dm$才能击中昆虫。
8 [新考法][2024石家庄外国语教育集团期末]小明和小强做弹球游戏,如图1,小明向斜坡抛一乒乓球,乒乓球弹起的运行路线是一条抛物线,乒乓球落地后又弹起,第二次弹起的运行路线和第一次运行路线的抛物线形状相同. 小强在地面立一块高度为0.4 m的木板$CD$,以斜坡底端$O$为坐标原点,地面水平线为$x$轴,取单位长度为1 m,建立如图2所示的平面直角坐标系,乒乓球的大小忽略不计,经测量发现,抛球点$A$的坐标为( - 1,3.36),第一次弹起的运行路线最高点坐标为( - 0.5,3.61),第二次弹起的最大高度为1.21 m.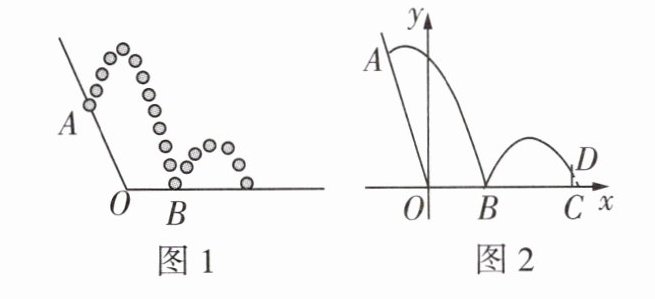
(1)乒乓球第一次落地点$B$距斜坡底端$O$的距离是______m;
(2)为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端$O$的最小距离是__________m.

(1)乒乓球第一次落地点$B$距斜坡底端$O$的距离是______m;
(2)为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端$O$的最小距离是__________m.
答案:
(1) 乒乓球第一次弹起运行路线的抛物线顶点为$(-0.5,3.61)$,过点$A(-1,3.36)$,所以设第一次运行路线所在的抛物线表达式为$y_{1}=a(x + 0.5)^{2}+3.61$。将点$A(-1,3.36)$的坐标代入,得$3.36 = a(-1 + 0.5)^{2}+3.61$,解得$a = -1$,所以$y_{1}=-(x + 0.5)^{2}+3.61$,令$y_{1}=0$,则$-(x + 0.5)^{2}+3.61 = 0$,解得$x_{1}=1.4$,$x_{2}=-2.4$(舍去),所以$OB = 1.4m$,即乒乓球第一次落地点$B$距斜坡底端$O$的距离为$1.4m$。
(2) 因为乒乓球第二次弹起运行路线的抛物线与第一次形状相同,且最大高度为$1.21m$,所以设$y_{2}=-(x - h)^{2}+1.21$。将点$B(1.4,0)$的坐标代入,得$0 = -(1.4 - h)^{2}+1.21$。解得$h_{1}=2.5$,$h_{2}=0.3$(舍去),所以$y_{2}=-(x - 2.5)^{2}+1.21$。当$y_{2}=0.4$时,$-(x - 2.5)^{2}+1.21 = 0.4$,解得$x_{1}=3.4$,$x_{2}=1.6$(舍去),所以为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端$O$的最小距离是$3.4m$。
(1) 乒乓球第一次弹起运行路线的抛物线顶点为$(-0.5,3.61)$,过点$A(-1,3.36)$,所以设第一次运行路线所在的抛物线表达式为$y_{1}=a(x + 0.5)^{2}+3.61$。将点$A(-1,3.36)$的坐标代入,得$3.36 = a(-1 + 0.5)^{2}+3.61$,解得$a = -1$,所以$y_{1}=-(x + 0.5)^{2}+3.61$,令$y_{1}=0$,则$-(x + 0.5)^{2}+3.61 = 0$,解得$x_{1}=1.4$,$x_{2}=-2.4$(舍去),所以$OB = 1.4m$,即乒乓球第一次落地点$B$距斜坡底端$O$的距离为$1.4m$。
(2) 因为乒乓球第二次弹起运行路线的抛物线与第一次形状相同,且最大高度为$1.21m$,所以设$y_{2}=-(x - h)^{2}+1.21$。将点$B(1.4,0)$的坐标代入,得$0 = -(1.4 - h)^{2}+1.21$。解得$h_{1}=2.5$,$h_{2}=0.3$(舍去),所以$y_{2}=-(x - 2.5)^{2}+1.21$。当$y_{2}=0.4$时,$-(x - 2.5)^{2}+1.21 = 0.4$,解得$x_{1}=3.4$,$x_{2}=1.6$(舍去),所以为了确保乒乓球在第二次下落时能落在木板上,小强将木板立在到斜坡底端$O$的最小距离是$3.4m$。
9 [新考法 模型观念][2023贵州中考]如图1是一座抛物线形拱桥,小星学习二次函数后,受到该图启示设计了一建筑物造型,它的截面图是抛物线的一部分(如图2所示),抛物线的顶点在$C$处,对称轴$OC$与水平线$OA$垂直,$OC = 9$,点$A$在抛物线上,且点$A$到对称轴的距离$OA = 3$,点$B$在抛物线上,点$B$到对称轴的距离是1.
(1)求抛物线的表达式;
(2)如图2,为更加稳固,小星想在$OC$上找一点$P$,加装拉杆$PA$,$PB$,同时使拉杆的长度之和最短,请你帮小星找到点$P$的位置并求出坐标;
(3)为了使造型更加美观,小星重新设计抛物线,其表达式为$y = - x^{2} + 2bx + b - 1(b \gt 0)$,当$4\leqslant x\leqslant 6$时,函数$y$的值总大于等于9,求$b$的取值范围.
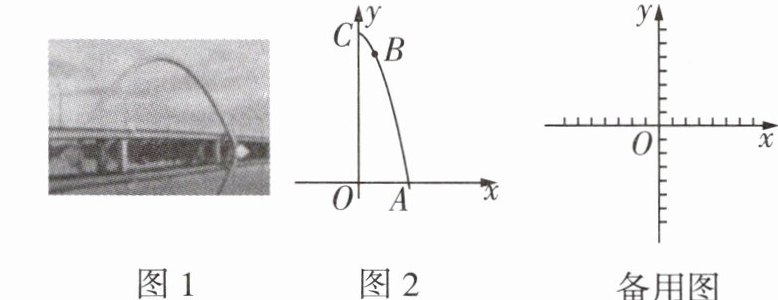
(1)求抛物线的表达式;
(2)如图2,为更加稳固,小星想在$OC$上找一点$P$,加装拉杆$PA$,$PB$,同时使拉杆的长度之和最短,请你帮小星找到点$P$的位置并求出坐标;
(3)为了使造型更加美观,小星重新设计抛物线,其表达式为$y = - x^{2} + 2bx + b - 1(b \gt 0)$,当$4\leqslant x\leqslant 6$时,函数$y$的值总大于等于9,求$b$的取值范围.

答案:
解题思路:
(1) 根据题意,设抛物线的表达式为$y = ax^{2}+9$,用待定系数法求解即可;
(2) 作点$A$关于$y$轴的对称点$A'$,连接$A'B$交$OC$于点$P$,则点$P$即为所求;
(3) 分$0\lt b\leqslant4$,$4\lt b\lt6$,$b\geqslant6$三种情况进行分类讨论,结合二次函数的图像和性质,建立不等式求得$b$的取值范围。 解:
(1) 设抛物线的表达式为$y = ax^{2}+9$,把点$A(3,0)$的坐标代入,得$9a + 9 = 0$,解得$a = -1$。所以抛物线的表达式为$y = -x^{2}+9$。
(2) 如图,作点$A$关于$y$轴的对称点$A'$,连接$A'B$交$OC$于点$P$,则点$P$即为所求,$A'(-3,0)$。把$x = 1$代入$y = -x^{2}+9$,得$y = 8$,所以$B(1,8)$。设直线$A'B$的表达式为$y = kx + m$,所以$\begin{cases}-3k + m = 0\\k + m = 8\end{cases}$,解得$\begin{cases}k = 2\\m = 6\end{cases}$,所以$y = 2x + 6$。令$x = 0$,得$y = 6$,所以点$P$的坐标为$(0,6)$。
(3)$y = -x^{2}+2bx + b - 1=-(x - b)^{2}+b^{2}+b - 1$,所以抛物线的对称轴为直线$x = b$,顶点坐标为$(b,b^{2}+b - 1)$。当$0\lt b\leqslant4$时,由$-6^{2}+12b + b - 1\geqslant9$,解得$b\geqslant\frac{46}{13}$,所以$\frac{46}{13}\leqslant b\leqslant4$。当$4\lt b\lt6$时,由$b - 4\gt6 - b$,得$b\gt5$,所以$-4^{2}+8b + b - 1\geqslant9$(抛物线开口向下,点离对称轴的距离越远,对应的函数值越小),解得$b\geqslant\frac{26}{9}$,所以$5\lt b\lt6$。由$b - 4\leqslant6 - b$,得$b\leqslant5$,所以$-6^{2}+12b + b - 1\geqslant9$,解得$b\geqslant\frac{46}{13}$,所以$4\lt b\leqslant5$。所以当$4\lt b\lt6$时,都成立。当$b\geqslant6$时,由$-4^{2}+8b + b - 1\geqslant9$,解得$b\geqslant\frac{26}{9}$,所以$b\geqslant6$都成立。综上所述,$b$的取值范围为$b\geqslant\frac{46}{13}$。
解题思路:
(1) 根据题意,设抛物线的表达式为$y = ax^{2}+9$,用待定系数法求解即可;
(2) 作点$A$关于$y$轴的对称点$A'$,连接$A'B$交$OC$于点$P$,则点$P$即为所求;
(3) 分$0\lt b\leqslant4$,$4\lt b\lt6$,$b\geqslant6$三种情况进行分类讨论,结合二次函数的图像和性质,建立不等式求得$b$的取值范围。 解:
(1) 设抛物线的表达式为$y = ax^{2}+9$,把点$A(3,0)$的坐标代入,得$9a + 9 = 0$,解得$a = -1$。所以抛物线的表达式为$y = -x^{2}+9$。
(2) 如图,作点$A$关于$y$轴的对称点$A'$,连接$A'B$交$OC$于点$P$,则点$P$即为所求,$A'(-3,0)$。把$x = 1$代入$y = -x^{2}+9$,得$y = 8$,所以$B(1,8)$。设直线$A'B$的表达式为$y = kx + m$,所以$\begin{cases}-3k + m = 0\\k + m = 8\end{cases}$,解得$\begin{cases}k = 2\\m = 6\end{cases}$,所以$y = 2x + 6$。令$x = 0$,得$y = 6$,所以点$P$的坐标为$(0,6)$。
(3)$y = -x^{2}+2bx + b - 1=-(x - b)^{2}+b^{2}+b - 1$,所以抛物线的对称轴为直线$x = b$,顶点坐标为$(b,b^{2}+b - 1)$。当$0\lt b\leqslant4$时,由$-6^{2}+12b + b - 1\geqslant9$,解得$b\geqslant\frac{46}{13}$,所以$\frac{46}{13}\leqslant b\leqslant4$。当$4\lt b\lt6$时,由$b - 4\gt6 - b$,得$b\gt5$,所以$-4^{2}+8b + b - 1\geqslant9$(抛物线开口向下,点离对称轴的距离越远,对应的函数值越小),解得$b\geqslant\frac{26}{9}$,所以$5\lt b\lt6$。由$b - 4\leqslant6 - b$,得$b\leqslant5$,所以$-6^{2}+12b + b - 1\geqslant9$,解得$b\geqslant\frac{46}{13}$,所以$4\lt b\leqslant5$。所以当$4\lt b\lt6$时,都成立。当$b\geqslant6$时,由$-4^{2}+8b + b - 1\geqslant9$,解得$b\geqslant\frac{26}{9}$,所以$b\geqslant6$都成立。综上所述,$b$的取值范围为$b\geqslant\frac{46}{13}$。

查看更多完整答案,请扫码查看


