《2025年一遍过九年级数学下册冀教版》

1 [2024邯郸育英学校检测]如图，PA，PB是⊙O的切线，切点为A，B，且∠APB = 40°，下列说法不正确的是 （ ）

A. PA = PB
B. ∠APO = 20°
C. ∠OBP = 70°
D. ∠AOP = 70°

答案： C@@因为 $PA$，$PB$ 是 $\odot O$ 的切线，且 $\angle APB = 40^{\circ}$，所以 $PA = PB$，$\angle APO=\angle BPO = 20^{\circ}$，$\angle PAO=\angle PBO = 90^{\circ}$，所以 $\angle BOP=\angle AOP = 70^{\circ}$。 **归纳总结**
(1) 经过圆外一点作圆的两条切线，切线长相等；
(2) 圆外一点与圆心的连线平分由该点所作圆的两切线的夹角。

2 [2023福州十六中期末]如图，已知PA，PB分别切⊙O于点A，B，∠P = 60°，PA = 8，那么弦AB的长是 （ ）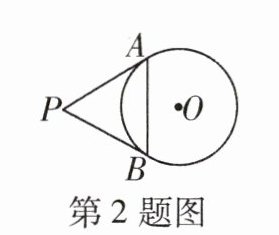
A. 4
B. 8
C. 4√3
D. 8√3

答案： B
@@因为 $PA$，$PB$ 分别切 $\odot O$ 于点 $A$，$B$，所以 $PA = PB$，又因为 $\angle P = 60^{\circ}$，所以 $\triangle APB$ 是等边三角形，所以 $AB = PA = 8$。
@@

[变式][2023廊坊期末]如图，在□APBC中，∠C = 40°. 若⊙O与PA，PB分别相切于点A，B，则∠CAB = （ ）

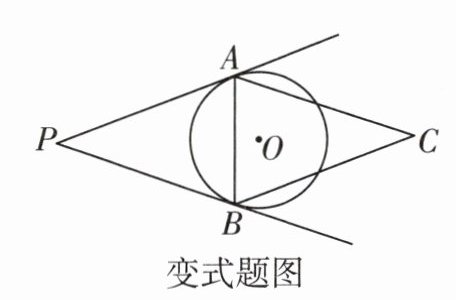
A. 40°
B. 50°
C. 60°
D. 70°

答案： D
@@因为 $\odot O$ 与 $PA$，$PB$ 分别相切于点 $A$，$B$，所以 $PA = PB$，又因为四边形 $APBC$ 是平行四边形，所以四边形 $APBC$ 是菱形，所以 $\angle P=\angle C = 40^{\circ}$，$\angle PAC = 140^{\circ}$，所以 $\angle CAB=\frac{1}{2}\angle PAC = 70^{\circ}$。

3 [教材P12例1变式][2023河北工程大学附属学校期末]如图，PA，PB，DE分别切⊙O于点A，B，C. 若⊙O的半径为6，OP = 10，则△PDE的周长为________.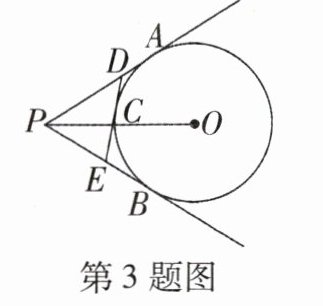

答案： 16@@连接 $OA$。因为 $PA$，$PB$，$DE$ 分别切 $\odot O$ 于点 $A$，$B$，$C$，所以 $AD = CD$，$CE = BE$，$PA = PB$，$OA\perp AP$。在 $Rt\triangle OAP$ 中，$AP=\sqrt{OP^{2}-OA^{2}}=\sqrt{10^{2}-6^{2}} = 8$，所以 $\triangle PDE$ 的周长为 $PD + DE+PE = PD + DC + CE + PE = PD + AD + BE + PE = AP + BP = 2AP = 16$。

4 如图，在△ABC中，AG平分∠CAB，使用尺规作射线CD，与AG，AB分别交于点E，D，下列判断正确的是 （ ）

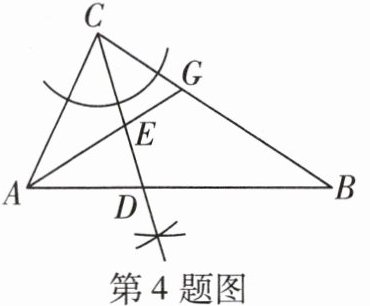
A. AG平分CD
B. ∠AED = ∠ADE
C. 点E是△ABC的内心
D. 点E到点A，B，C的距离相等

答案： C@@由题图作法得 $CD$ 平分 $\angle ACB$，又因为 $AG$ 平分 $\angle CAB$，所以点 $E$ 为 $\triangle ABC$ 的内心。

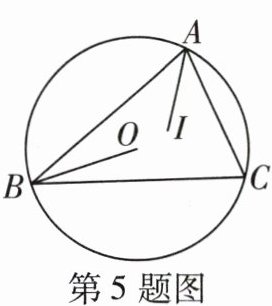
5 [2023聊城中考]如图，点O是△ABC外接圆的圆心，点I是△ABC的内心，连接OB，IA. 若∠CAI = 35°，则∠OBC的度数为 （ ）

A. 15°
B. 17.5°
C. 20°
D. 25°

答案： C@@如图，连接 $OC$，因为点 $I$ 是 $\triangle ABC$ 的内心，所以 $AI$ 平分 $\angle BAC$。因为 $\angle CAI = 35^{\circ}$，所以 $\angle BAC = 2\angle CAI = 70^{\circ}$。因为点 $O$ 是 $\triangle ABC$ 外接圆的圆心，所以 $\angle BOC = 2\angle BAC = 140^{\circ}$（圆上一条弧所对的圆周角等于它所对的圆心角的一半）。因为 $OB = OC$，所以 $\angle OBC=\angle OCB=\frac{1}{2}\times(180^{\circ}-\angle BOC)=\frac{1}{2}\times(180^{\circ}-140^{\circ}) = 20^{\circ}$。

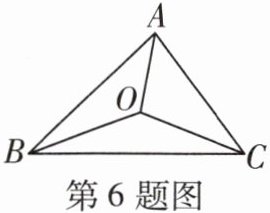
6 [2024石家庄十七中二模]如图，在△ABC中，AB = 8，AC = 6，O为△ABC的内心. 若△ABO的面积为20，则△ACO的面积为 （ ）

A. 20
B. 15
C. 18
D. 12

答案： B@@因为 $O$ 为 $\triangle ABC$ 的内心，所以点 $O$ 到 $AB$，$AC$ 的距离相等，所以 $S_{\triangle AOB}:S_{\triangle AOC}=AB:AC = 8:6 = 4:3$（两三角形的高相等，则两三角形的面积比等于两底边长的比）。因为 $\triangle ABO$ 的面积为 $20$，所以 $\triangle ACO$ 的面积为 $15$。

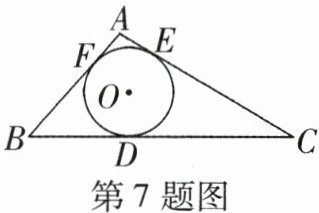
7 [2024张家口博文实验中学期末]如图，⊙O是△ABC的内切圆，分别切BC，AC，AB于点D，E，F，△ABC的周长为24 cm，BC = 10 cm，则AE = ________cm.

答案： 2@@因为 $\odot O$ 是 $\triangle ABC$ 的内切圆，分别切 $BC$，$AC$，$AB$ 于点 $D$，$E$，$F$，所以 $AF = AE$，$BD = BF$，$CE = CD$，根据题意得 $\begin{cases}2AE + 2BD+2DC = 24\mathrm{cm},\\BD + DC = 10\mathrm{cm},\end{cases}$ 所以 $AE = 2\mathrm{cm}$。

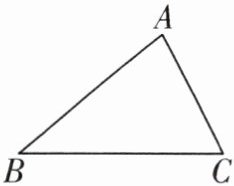
8 如图，已知△ABC，∠B = 40°.
（1）在图中用尺规作出△ABC的内切圆⊙O，并标出⊙O与边AB，BC，AC的切点D，E，F（保留作图痕迹，不必写作法）；
（2）连接EF，DF，求∠EFD的度数.

答案： 解：
(1) 如图，$\odot O$ 即所求。
(2) 如图，连接 $OD$，$OE$，由题意知 $OD\perp AB$，$OE\perp BC$，所以 $\angle ODB=\angle OEB = 90^{\circ}$。因为 $\angle B = 40^{\circ}$，所以 $\angle DOE = 140^{\circ}$，所以 $\angle EFD=\frac{1}{2}\angle DOE = 70^{\circ}$。