《2025年一遍过九年级数学下册冀教版》

6 [2024天津红桥区二模]如图,有一块矩形空地ABCD,学校规划在其中间的一块四边形空地EFGH上种花,其余的四块三角形空地上铺设草坪,其中点E,F,G,H分别在边AD,AB,BC,CD上,且AE = AF = CG = CH. 已知AD = 20 m,AB = 40 m,则种花的最大面积为( )

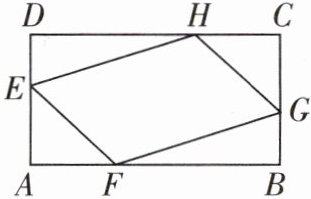
A. 400 m²
B. 450 m²
C. 500 m²
D. 900 m²

答案： B 设AE = x m，则ED = (20 - x)m，DH = (40 - x)m，设种花的面积为y m²，则$y = 20×40 - 2×\frac{1}{2}(40 - x)(20 - x)-2×\frac{1}{2}x^2 = 800 - 800 + 60x - 2x^2=-2x^2 + 60x=-2(x - 15)^2 + 450$，因为-2 ＜ 0，所以当x = 15时，y有最大值，最大值为450，则种花的最大面积为450 m²。

7 [2024遂宁中考改编]某酒店有A种客房24间,每间A种客房定价为200元. 酒店对A种客房调研发现:如果不调价,房间可全部住满;如果每个房间定价每增加10元,就会有一个房间空闲;当A种客房每间定价为________元时,A种客房一天的营业额W(元)最大,最大营业额为________元.

答案： 220 4840 设A种客房每间定价为a元，则$W=(24-\frac{a - 200}{10})a=-\frac{1}{10}a^2 + 44a=-\frac{1}{10}(a - 220)^2 + 4840$，因为$-\frac{1}{10}＜0$，所以当a = 220时，W取最大值，$W_{最大值}=4840$。

8 [2023唐山模拟]如图,在矩形纸片ABCD中,AB = 3,BC = 2,沿对角线AC剪开(如图1);固定△ADC,把△ABC沿AD方向平移(如图2),当两个三角形重叠部分的面积最大时,移动的距离AA'等于________.

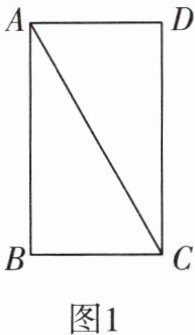
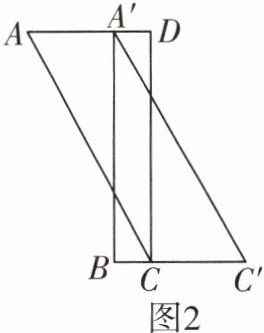
答案：
1 设A'B'交AC于点E，AA' = x，A'D = 2 - x，根据$tan∠DAC=\frac{DC}{AD}=\frac{A'E}{AA'}$，AD = 2，DC = 3，可得$\frac{3}{2}=\frac{A'E}{x}$，$A'E=\frac{3}{2}x$。 当x = 1时，重叠部分的面积最大，两个三角形重叠部分的面积$S = A'E·A'D=\frac{3}{2}x(2 - x)=-\frac{3}{2}(x - 1)^2+\frac{3}{2}$。

9 [2023南充中考]某工厂计划从A,B两种产品中选择一种生产并销售,每日产销x件. 已知A产品成本价为m元/件(m为常数,且4≤m≤6),售价为8元/件,每日最多产销500件,同时每日共支付专利费30元;B产品成本价为12元/件,售价为20元/件,每日最多产销300件,同时每日支付专利费y元,y(元)与每日产销x(件)满足关系式y = 80 + 0.01x².
(1)若产销A,B两种产品的日利润分别为w₁元、w₂元,请分别写出w₁,w₂与x的函数关系式,并写出x的取值范围.
(2)分别求出产销A,B两种产品的最大日利润. (A产品的最大日利润用含m的代数式表示)
(3)为获得最大日利润,该工厂应该选择产销哪种产品? 并说明理由.
【利润 = (售价 - 成本)×产销数量 - 专利费】

答案： 解：
(1)根据题意，得$w_1=(8 - m)x - 30(0≤x≤500)$，$w_2=(20 - 12)x-(80 + 0.01x^2)=-0.01x^2 + 8x - 80(0≤x≤300)$。
(2)因为8 - m ＞ 0，所以$w_1$随x的增大而增大， 又因为0 ≤ x ≤ 500， 所以当x = 500时，$w_1$有最大值，$w_{1最大}=-500m + 3970$。 $w_2=-0.01x^2 + 8x - 80=-0.01(x - 400)^2 + 1520$， 因为-0.01 ＜ 0，函数图像的对称轴为直线x = 400， 所以当0 ≤ x ≤ 300时，$w_2$随x的增大而增大， 所以当x = 300时，$w_2$有最大值，$w_{2最大}=-0.01×(300 - 400)^2 + 1520 = 1420$。
(3)①若$w_{1最大}=w_{2最大}$，即-500m + 3970 = 1420，解得m = 5.1； ②若$w_{1最大}＞w_{2最大}$，即-500m + 3970 ＞ 1420，解得m ＜ 5.1； ③若$w_{1最大}＜w_{2最大}$，即-500m + 3970 ＜ 1420，解得m ＞ 5.1。 因为4 ≤ m ≤ 6，所以为获得最大日利润， 当m = 5.1时，该工厂选择A，B产品产销均可； 当4 ≤ m ＜ 5.1时，该工厂选择A产品产销； 当5.1 ＜ m ≤ 6时，该工厂选择B产品产销。

10 [应用意识][2024自贡中考]九(1)班劳动实践基地内有一块面积足够大的平整空地. 地上两段围墙AB⊥CD于点O(如图),其中AB上的EO段围墙空缺. 同学们测得AE = 6.6 m,OE = 1.4 m,OB = 6 m,OC = 5 m,OD = 3 m. 班长买来可切断的围栏16 m,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是________m².

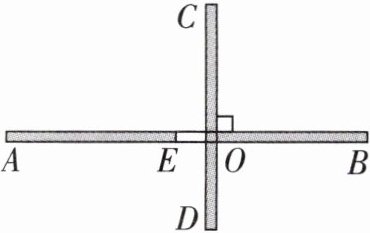
答案：
46.4 要使该矩形菜地面积最大，则要利用AO和OC构成矩形。设矩形在射线OA上的一段长为x m，矩形菜地面积为S。当x ≤ 8时，如图1，则在射线OC上的长为$\frac{16 - x - 1.4 + 5}{2}=\frac{19.6 - x}{2}$，所以$S = x·\frac{19.6 - x}{2}=-\frac{1}{2}x^2 + 9.8x=-\frac{1}{2}(x - 9.8)^2 + 48.02$，因为$-\frac{1}{2}＜0$，所以当x ≤ 9.8时，S随x的增大而增大，所以当x = 8时，S取最大值，最大值为46.4；当x ＞ 8时，如图2，则矩形菜园的总长为(16 + 6.6 + 5)=27.6 m，则在射线OC上的长为$\frac{27.6 - 2x}{2}$，所以$S = x(13.8 - x)=-x^2 + 13.8x=-(x - 6.9)^2 + 47.61$，因为-1 ＜ 0，所以当x ＞ 6.9时，S随x的增大而减少，可得当x ＞ 8时，S的值均小于46.4。综上，矩形菜地的最大面积是46.4 m²。