《2025年一遍过九年级数学下册冀教版》

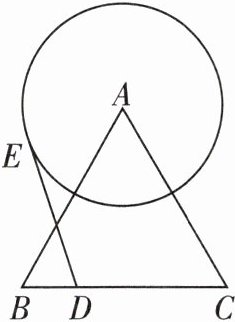
1 [2023徐州期末]如图，等边三角形ABC的边长为4，⊙A的半径为2，D是BC上的动点，DE与⊙A相切于点E，则DE的最小值是（ ）

A. 2
B. $\sqrt{11}$
C. $2\sqrt{2}$
D. 3

答案：
C@@：如图，连接$AE$，$AD$，过点$A$作$AH\perp BC$于$H$。因为$DE$与$\odot A$相切于$E$，所以$AE\perp DE$。又因为$\odot A$的半径为$2$，所以$DE = \sqrt{AD^{2}-AE^{2}}=\sqrt{AD^{2}-2^{2}}$。当$D$与$H$重合时，$AD$最小。由于等边三角形$ABC$的边长为$4$，所以$BH = CH = 2$，$AH=\sqrt{AB^{2}-BH^{2}}=\sqrt{4^{2}-2^{2}} = 2\sqrt{3}$，则$DE$的最小值为$\sqrt{(2\sqrt{3})^{2}-2^{2}}=2\sqrt{2}$。

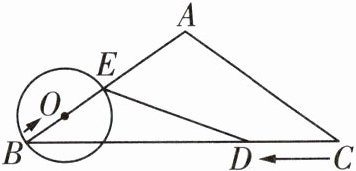
2 如图，在等腰三角形ABC中，AB = AC = 5 cm，BC = 8 cm. 动点D从点C出发，沿线段CB以2 cm/s的速度向点B运动，同时动点O从点B出发，沿线段BA以1 cm/s的速度向点A运动，当其中一个动点停止运动时另一个动点也随之停止运动. 设运动时间为t s，以点O为圆心、OB的长为半径的⊙O与BA交于另一点E，连接ED. 当DE与⊙O相切时，t的值是（ ）

A. $\frac{16}{9}$
B. $\frac{3}{2}$
C. $\frac{1}{2}$
D. $\sqrt{3}$

答案： A@@：过点$A$作$AH\perp BC$于$H$，由题意可知$BE = 2t\ cm$，$BD=(8 - 2t)\ cm$。因为$AB = AC = 5\ cm$，$BC = 8\ cm$，所以$BH = CH=\frac{1}{2}BC = 4\ cm$。当$BE\perp DE$时，$DE$与$\odot O$相切，则$\angle BED = 90^{\circ}$。因为$\angle EBD=\angle ABH$，$\angle BED=\angle BHA = 90^{\circ}$，所以$\triangle BED\sim\triangle BHA$，所以$\frac{BE}{BH}=\frac{BD}{BA}$，即$\frac{2t}{4}=\frac{8 - 2t}{5}$，解得$t=\frac{16}{9}$。

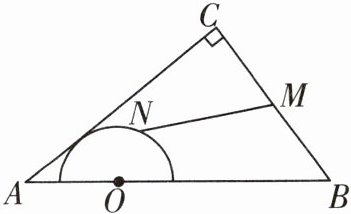
3 如图，在Rt△ABC中，∠C = 90°，AC = 4，BC = 3，O是AB的三等分点，半圆O与AC相切，M，N分别是BC与半圆弧上的动点，则MN的最小值和最大值之和是（ ）

A. 5
B. 6
C. 7
D. 8

答案：
B@@：如图，设半圆$O$与$AC$相切于点$D$，连接$OD$，过点$O$作$OP\perp BC$，垂足为点$P$，交半圆$O$于点$F$，此时垂线段$OP$最短，$PF$的长为$MN$的最小值。因为$AC = 4$，$BC = 3$，$\angle C = 90^{\circ}$，所以$AB = 5$。因为$\angle OPB = 90^{\circ}$，$\angle C = 90^{\circ}$，所以$OP// AC$，所以$\frac{OP}{AC}=\frac{OB}{AB}$。因为$O$是$AB$的三等分点，所以$\frac{OP}{AC}=\frac{OB}{AB}=\frac{2}{3}$，所以$OP=\frac{8}{3}$。因为半圆$O$与$AC$相切于点$D$，所以$OD\perp AC$，所以$OD// BC$，所以$\frac{OD}{BC}=\frac{OA}{AB}=\frac{1}{3}$，所以$OD = 1$，所以$MN$的最小值为$OP - OF=\frac{8}{3}-1=\frac{5}{3}$。当$N$与$E$重合，$M$与$B$重合时，$OM$最长，且$OM$，$ON$共线，此时$MN$最长，则$MN$的最大值为$\frac{10}{3}+1=\frac{13}{3}$，所以$MN$的最大值与最小值之和是$6$。!

4 [新情境][2023泰州模拟]燃油机由汽缸、活塞A、连杆AP、曲轴OP、飞轮⊙O组成（如图所示），活塞A在汽缸内往复运动，通过连杆AP带动曲轴OP作圆周运动，其中AP = 70 cm，OP = 30 cm，当A在初始位置A＜sub＞0＜/sub＞时，点O，P，A共线. 设点A从A＜sub＞0＜/sub＞向左移动的距离为d，曲轴OP绕点O逆时针旋转α，0° ＜ α≤180°.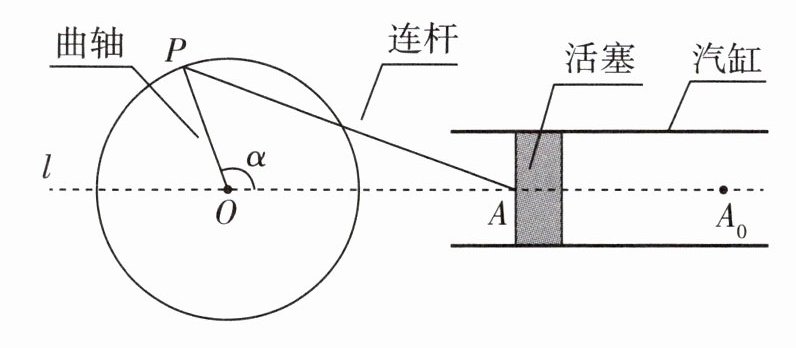
(1)d为多少时，AP与点P所在的⊙O相切?
(2)若d = 50 cm，求点P经过的路线长.

答案：
解： - （1）如图1，因为$AP$与点$P$所在的$\odot O$相切，所以$\angle OPA = 90^{\circ}$。因为$AP = 70\ cm$，$OP = 30\ cm$，所以$OA=\sqrt{OP^{2}+PA^{2}} = 10\sqrt{58}\ cm$，所以$d = AA_{0}=OA_{0}-OA=(100 - 10\sqrt{58})(cm)$。! - （2）当$d = 50\ cm$时，如图2，过点$P$作$PH\perp l$于点$H$，设$OH = x\ cm$，所以$d = OA_{0}-OA = 50\ cm$，此时$OA = 100 - 50 = 50(cm)$。由勾股定理，得$OP^{2}-OH^{2}=AP^{2}-AH^{2}$，即$30^{2}-x^{2}=70^{2}-(50 + x)^{2}$，解得$x = 15$。在$Rt\triangle PHO$中，$\cos\angle POH=\frac{OH}{PO}=\frac{15}{30}=\frac{1}{2}$，所以$\angle POH = 60^{\circ}$，所以$\angle POA = 120^{\circ}$，所以点$P$经过的路线长为$\frac{120\pi\times30}{180}=20\pi(cm)$。!