第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
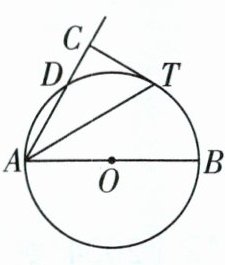
1 [母题·教材P23T4节选]如图,AB是⊙O的直径,CT与⊙O相切,且AC与CT垂直,AC交⊙O于点D. 求证:AT平分∠BAD.

答案:
证明:连接OT,如图,因为CT与⊙O相切,所以∠OTC = 90°,因为OA = OT,所以∠OAT = ∠OTA = 90° - ∠ATC,因为AC⊥CT,所以∠CAT = 90° - ∠ATC,所以∠OAT = ∠CAT,所以AT平分∠BAD。
证明:连接OT,如图,因为CT与⊙O相切,所以∠OTC = 90°,因为OA = OT,所以∠OAT = ∠OTA = 90° - ∠ATC,因为AC⊥CT,所以∠CAT = 90° - ∠ATC,所以∠OAT = ∠CAT,所以AT平分∠BAD。

2 [条件与结论互换证垂直]如图,AB是⊙O的直径,F为⊙O上一点,AC平分∠FAB且交⊙O于点C,过点C作⊙O的切线交AF的延长线于点D. 求证:AD⊥CD.


答案:
证明:如图,连接OC。因为OA = OC,所以∠CAO = ∠OCA,因为AC平分∠FAB,所以∠DAC = ∠CAO,所以∠DAC = ∠OCA,所以AD//OC,因为CD是⊙O的切线,所以OC⊥CD,所以AD⊥CD。
证明:如图,连接OC。因为OA = OC,所以∠CAO = ∠OCA,因为AC平分∠FAB,所以∠DAC = ∠CAO,所以∠DAC = ∠OCA,所以AD//OC,因为CD是⊙O的切线,所以OC⊥CD,所以AD⊥CD。

3 [条件与结论互换证切线][2023阳江期末]如图,在Rt△ABC中,∠C = 90°,点E在边AB上,以AE为直径的⊙O与BC有公共点D,且AD平分∠BAC.
(1)求证:BC与⊙O相切.
(2)若AC = 4,AD = 2√6,求⊙O的半径.

(1)求证:BC与⊙O相切.
(2)若AC = 4,AD = 2√6,求⊙O的半径.

答案:
- 解题思路: - (1)连接OD,可证明∠ODA = ∠DAB = ∠DAC,所以OD//AC,所以∠ODB = ∠C = 90°,即可证明BC与⊙O相切; - (2)过点O作OF⊥AC于点F,根据矩形的性质和勾股定理求解,设OD = OA = r,则CF = OD = r,可列方程(4 - r)² + (2√2)² = r²,解方程求出r的值即可。 - (1)证明:如图,连接OD,则OD = OA,所以∠ODA = ∠DAB,因为AD平分∠BAC,所以∠DAC = ∠DAB,所以∠ODA = ∠DAC,所以OD//AC,所以∠ODB = ∠C = 90°,因为BC经过⊙O的半径OD的外端,且BC⊥OD,所以BC与⊙O相切。! - (2)解:如图,过点O作OF⊥AC于点F,因为∠OFC = ∠C = ∠ODC = 90°,所以四边形ODCF是矩形,所以OD = CF,OF = CD。因为AC = 4,AD = 2√6,所以OF = CD = √(AD² - AC²) = 2√2,设OD = OA = r,则CF = r,AF = 4 - r。在Rt△AOF中,由勾股定理,得AF² + OF² = OA²,所以(4 - r)² + (2√2)² = r²,解得r = 3,所以⊙O的半径为3。
- (2)解:如图,过点O作OF⊥AC于点F,因为∠OFC = ∠C = ∠ODC = 90°,所以四边形ODCF是矩形,所以OD = CF,OF = CD。因为AC = 4,AD = 2√6,所以OF = CD = √(AD² - AC²) = 2√2,设OD = OA = r,则CF = r,AF = 4 - r。在Rt△AOF中,由勾股定理,得AF² + OF² = OA²,所以(4 - r)² + (2√2)² = r²,解得r = 3,所以⊙O的半径为3。
- 解题思路: - (1)连接OD,可证明∠ODA = ∠DAB = ∠DAC,所以OD//AC,所以∠ODB = ∠C = 90°,即可证明BC与⊙O相切; - (2)过点O作OF⊥AC于点F,根据矩形的性质和勾股定理求解,设OD = OA = r,则CF = OD = r,可列方程(4 - r)² + (2√2)² = r²,解方程求出r的值即可。 - (1)证明:如图,连接OD,则OD = OA,所以∠ODA = ∠DAB,因为AD平分∠BAC,所以∠DAC = ∠DAB,所以∠ODA = ∠DAC,所以OD//AC,所以∠ODB = ∠C = 90°,因为BC经过⊙O的半径OD的外端,且BC⊥OD,所以BC与⊙O相切。!
 - (2)解:如图,过点O作OF⊥AC于点F,因为∠OFC = ∠C = ∠ODC = 90°,所以四边形ODCF是矩形,所以OD = CF,OF = CD。因为AC = 4,AD = 2√6,所以OF = CD = √(AD² - AC²) = 2√2,设OD = OA = r,则CF = r,AF = 4 - r。在Rt△AOF中,由勾股定理,得AF² + OF² = OA²,所以(4 - r)² + (2√2)² = r²,解得r = 3,所以⊙O的半径为3。
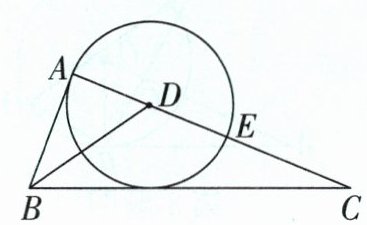
- (2)解:如图,过点O作OF⊥AC于点F,因为∠OFC = ∠C = ∠ODC = 90°,所以四边形ODCF是矩形,所以OD = CF,OF = CD。因为AC = 4,AD = 2√6,所以OF = CD = √(AD² - AC²) = 2√2,设OD = OA = r,则CF = r,AF = 4 - r。在Rt△AOF中,由勾股定理,得AF² + OF² = OA²,所以(4 - r)² + (2√2)² = r²,解得r = 3,所以⊙O的半径为3。 4 [变为直角三角形的直角边过圆心]如图,在Rt△ABC中,∠BAC = 90°,BD是角平分线,以D为圆心、DA的长为半径的⊙D与AC交于点E.
(1)求证:BC与⊙D相切.
(2)若sin C = 5/13,设BC切⊙D于点F,求tan∠CFE的值.
(1)求证:BC与⊙D相切.
(2)若sin C = 5/13,设BC切⊙D于点F,求tan∠CFE的值.

答案:
- (1)证明:过点D作DM⊥BC于点M,如图1。因为∠BAD = 90°,所以AD⊥AB,因为BD平分∠ABC,DA⊥AB,DM⊥BC,所以AD = DM。又因为DM⊥BC,所以BC与⊙D相切。! - (2)解:连接DF,EF,过点E作EG⊥FC于点G,如图2。设DF = 5k,由题意知DF⊥BC,因为sin C = 5/13 = DF/DC,所以CD = 13k,所以FC = √(CD² - DF²) = 12k,CE = CD - DE = 8k。
- 解法一:因为DF⊥BC,EG⊥FC,所以EG//FD,所以△CEG∽△CDF,所以CE/CD = EG/DF = CG/CF,即8k/13k = EG/5k = CG/12k,所以EG = 40/13k,CG = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- 解法二:在Rt△CEG中,sin C = EG/CE = 5/13,所以EG = 40/13k,所以CG = √(CE² - EG²) = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- (2)解:连接DF,EF,过点E作EG⊥FC于点G,如图2。设DF = 5k,由题意知DF⊥BC,因为sin C = 5/13 = DF/DC,所以CD = 13k,所以FC = √(CD² - DF²) = 12k,CE = CD - DE = 8k。
- 解法一:因为DF⊥BC,EG⊥FC,所以EG//FD,所以△CEG∽△CDF,所以CE/CD = EG/DF = CG/CF,即8k/13k = EG/5k = CG/12k,所以EG = 40/13k,CG = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- 解法二:在Rt△CEG中,sin C = EG/CE = 5/13,所以EG = 40/13k,所以CG = √(CE² - EG²) = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- (1)证明:过点D作DM⊥BC于点M,如图1。因为∠BAD = 90°,所以AD⊥AB,因为BD平分∠ABC,DA⊥AB,DM⊥BC,所以AD = DM。又因为DM⊥BC,所以BC与⊙D相切。!
 - (2)解:连接DF,EF,过点E作EG⊥FC于点G,如图2。设DF = 5k,由题意知DF⊥BC,因为sin C = 5/13 = DF/DC,所以CD = 13k,所以FC = √(CD² - DF²) = 12k,CE = CD - DE = 8k。
- 解法一:因为DF⊥BC,EG⊥FC,所以EG//FD,所以△CEG∽△CDF,所以CE/CD = EG/DF = CG/CF,即8k/13k = EG/5k = CG/12k,所以EG = 40/13k,CG = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- 解法二:在Rt△CEG中,sin C = EG/CE = 5/13,所以EG = 40/13k,所以CG = √(CE² - EG²) = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- (2)解:连接DF,EF,过点E作EG⊥FC于点G,如图2。设DF = 5k,由题意知DF⊥BC,因为sin C = 5/13 = DF/DC,所以CD = 13k,所以FC = √(CD² - DF²) = 12k,CE = CD - DE = 8k。
- 解法一:因为DF⊥BC,EG⊥FC,所以EG//FD,所以△CEG∽△CDF,所以CE/CD = EG/DF = CG/CF,即8k/13k = EG/5k = CG/12k,所以EG = 40/13k,CG = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
- 解法二:在Rt△CEG中,sin C = EG/CE = 5/13,所以EG = 40/13k,所以CG = √(CE² - EG²) = 96/13k,所以FG = FC - GC = 60/13k,所以tan∠EFC = EG/FG = (40/13k)/(60/13k) = 2/3。
5 [变为直角三角形的斜边不过圆心][2023秦皇岛十月考]如图,半径为3的⊙O与Rt△ABC相交于点A,C,D,连接OD,AD,DA平分∠BDO,∠B = 90°.
(1)求证:AB与⊙O相切.
(2)若∠CAB = 65°,求⌢CD的长(结果保留π).
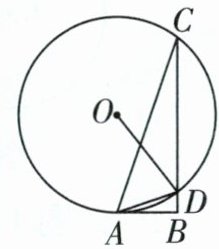
(1)求证:AB与⊙O相切.
(2)若∠CAB = 65°,求⌢CD的长(结果保留π).
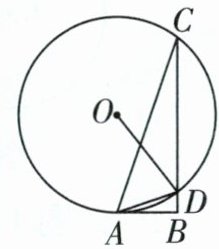
答案:
- (1)证明:连接OA,如图。因为OA = OD,所以∠OAD = ∠ODA。因为DA平分∠BDO,所以∠ADB = ∠ODA,所以∠OAD = ∠ADB,所以OA//BC,所以∠OAB + ∠B = 180°。因为∠B = 90°,所以∠OAB = 90°,又因为OA是⊙O的半径,所以AB与⊙O相切。! - (2)解:连接OC,如图,因为∠B = 90°,∠CAB = 65°,所以∠ACB = 25°,所以∠AOD = 50°。因为OA//BC,所以∠ODC = ∠AOD = 50°。因为OC = OD,所以∠OCD = ∠ODC = 50°,所以∠COD = 80°,所以弧CD的长为80π×3 / 180 = 4/3π。
- (2)解:连接OC,如图,因为∠B = 90°,∠CAB = 65°,所以∠ACB = 25°,所以∠AOD = 50°。因为OA//BC,所以∠ODC = ∠AOD = 50°。因为OC = OD,所以∠OCD = ∠ODC = 50°,所以∠COD = 80°,所以弧CD的长为80π×3 / 180 = 4/3π。
- (1)证明:连接OA,如图。因为OA = OD,所以∠OAD = ∠ODA。因为DA平分∠BDO,所以∠ADB = ∠ODA,所以∠OAD = ∠ADB,所以OA//BC,所以∠OAB + ∠B = 180°。因为∠B = 90°,所以∠OAB = 90°,又因为OA是⊙O的半径,所以AB与⊙O相切。!
 - (2)解:连接OC,如图,因为∠B = 90°,∠CAB = 65°,所以∠ACB = 25°,所以∠AOD = 50°。因为OA//BC,所以∠ODC = ∠AOD = 50°。因为OC = OD,所以∠OCD = ∠ODC = 50°,所以∠COD = 80°,所以弧CD的长为80π×3 / 180 = 4/3π。
- (2)解:连接OC,如图,因为∠B = 90°,∠CAB = 65°,所以∠ACB = 25°,所以∠AOD = 50°。因为OA//BC,所以∠ODC = ∠AOD = 50°。因为OC = OD,所以∠OCD = ∠ODC = 50°,所以∠COD = 80°,所以弧CD的长为80π×3 / 180 = 4/3π。 查看更多完整答案,请扫码查看


