《2025年一遍过九年级数学下册冀教版》

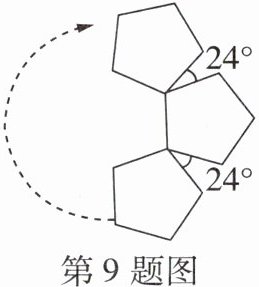
9 [2024 邯郸二模]如图，用一些全等的正五边形按如图方式可以拼成一个环状，使相邻的两个正五边形有公共顶点，所夹的锐角为 24°，图中所示的是前 3 个正五边形拼接的情况，拼接一圈后，中间会形成一个正多边形，则该正多边形的边数是 （ ）

A. 4
B. 5
C. 6
D. 7

答案： C
∵正五边形的每个内角为180°×(5 - 2)÷5 = 108°，
∴组成的正多边形的每个内角为360° - 2×108° - 24° = 120°。设n个全等的正五边形拼接可以拼成一个环状，则中间形成的正多边形为正n边形，则$\frac{(n - 2)×180°}{n}$ = 120°，解得n = 6。

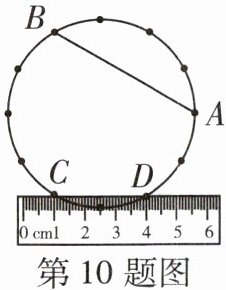
10 [新考法][2024 邢台一模]如图，A，B，C，D 为圆周上十二等分点中的四个点，若用直尺测量弦 CD 的长时，发现 C 点、D 点分别与刻度 1 和 4 对齐，则 A，B 两点的距离是 （ ）

A. 2$\sqrt{2}$
B. 2$\sqrt{3}$
C. 3$\sqrt{3}$
D. 6

答案：
C 如图，连接BD，BC，OC，由正十二边形及其外接圆的对称性可知，BD是⊙O的直径，
∴∠BCD = 90°，∠CBD = $\frac{1}{2}$∠COD = $\frac{360°}{12}$ = 30°。在Rt△BCD中，∠CBD = 30°，CD = 4 - 1 = 3，
∴BC = $\sqrt{3}$CD = 3$\sqrt{3}$，
∴AB = BC = 3$\sqrt{3}$。

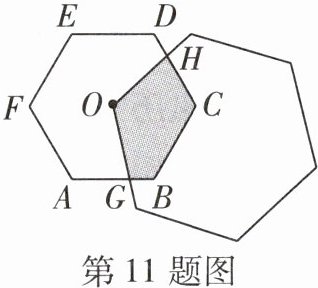
11 [2024 张家口宣化区一模]如图，一个适当大的正六边形，它的一个顶点与一个边长为定值的小正六边形 ABCDEF 的中心 O 重合，且与边 AB，CD 相交于点 G，H. 图中阴影部分的面积记为 S，三条线段 GB，BC，CH 的长度之和记为 l，在大正六边形绕点 O 旋转的过程中，下列说法正确的是 （ ）

A. S 变化，l 不变
B. S 不变，l 变化
C. S 变化，l 变化
D. S 与 l 均不变

答案：
D 如图，连接OA，OC，则∠OCH = ∠OAG = 60°，
∵∠HOG = ∠AOC = 120°，
∴∠HOC = ∠GOA。在△OHC和△OGA中，$\begin{cases}∠HOC = ∠GOA \\ OC = OA \\ ∠OCH = ∠OAG\end{cases}$，
∴△HOC ≌ △GOA（ASA），
∴CH = AG，
∴S阴影 = S四边形OABC，即阴影部分的面积S为定值。
∵l = GB + BC + CH = AG + GB + BC = 2BC，
∴l为定值。

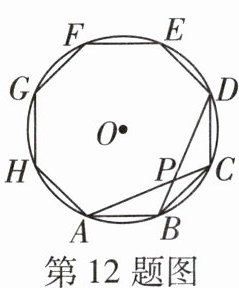
12 [2023 石家庄期末]如图所示，已知正八边形 ABCDEFGH 内接于⊙O，连接 AC，BD 相交于点 P. 若⊙O 的半径为 1，则 AC = ________，∠APD = ______°，△ABC 的面积为 ______.

答案：
$\sqrt{2}$ 135 $\frac{\sqrt{2}-1}{2}$ 解题思路：连接OA，OB，OB与AC交于点Q，先根据正八边形的性质求出∠AOB，再根据特殊角的三角函数值求出QB，AC的长，再根据圆周角定理和三角形的外角性质即可求出∠APD，最后根据三角形的面积公式求出△ABC的面积。 如图，连接OA，OB，OB与AC交于点Q，由题意可知，QA = QC，OB⊥AC，
∵八边形ABCDEFGH是正八边形，
∴∠AOB = $\frac{360°}{8}$ = 45°，
∴QA = OQ = OA·sin∠AOB = sin 45° = $\frac{\sqrt{2}}{2}$，
∴QB = OB - OQ = 1 - $\frac{\sqrt{2}}{2}$，AC = 2QA = $\sqrt{2}$。
∵$\overset{\frown}{AFD}$所对的圆心角为5∠AOB = 225°，
∴$\overset{\frown}{AFD}$所对的圆周角为∠ABD = $\frac{1}{2}$×225° = 112.5°，
∵∠BAC = $\frac{1}{2}$×45° = 22.5°，
∴∠APD = ∠ABD + ∠BAC = 135°，S△ABC = $\frac{1}{2}$AC·QB = $\frac{1}{2}$×$\sqrt{2}$×(1 - $\frac{\sqrt{2}}{2}$) = $\frac{\sqrt{2}-1}{2}$。

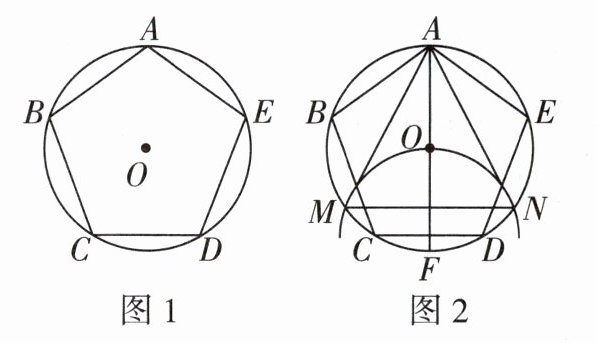
13 [2022 金华中考]如图 1，正五边形 ABCDE 内接于⊙O，阅读以下作图过程，并回答下列问题.
作法：如图 2.
1. 作直径 AF.
2. 以 F 为圆心，FO 的长为半径作圆弧，与⊙O 交于点 M，N.
3. 连接 AM，MN，NA.
（1）求∠ABC 的度数.
（2）△AMN 是正三角形吗？请说明理由.
（3）从点 A 开始，以 DN 长为半径，在⊙O 上依次截取点，再依次连接这些分点，得到正 n 边形，求 n 的值.

答案：
解：
(1)
∵五边形ABCDE是正五边形，
∴∠ABC = $\frac{(5 - 2)×180°}{5}$ = 108°。
(2)△AMN是正三角形。理由如下： 连接ON，NF，如图， 由题意可得，FN = ON = OF，
∴△FON是等边三角形，
∴∠NFA = 60°，
∴∠NMA = 60°， 同理可得，∠ANM = 60°，
∴∠MAN = 60°。
∴△AMN是正三角形。
(3)如图，连接OD。
∵∠AMN = 60°，
∴∠AON = 120°。
∵∠AOD = $\frac{360°}{5}$×2 = 144°，
∴∠NOD = ∠AOD - ∠AON = 144° - 120° = 24°。
∵360°÷24° = 15，
∴n的值是15。

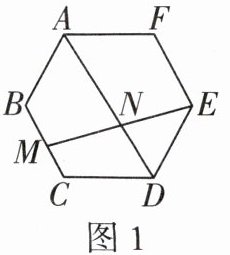
14 [几何直观][2024 衡水桃城中学二模]如图 1，在边长为 2 的正六边形 ABCDEF 中，M 是 BC 的中点，连接 EM 交 AD 于 N 点. 若 MN = a，则表示实数 a 的点落在数轴上（如图 2）标有序号四段中的 （ ）


A. 段①
B. 段②
C. 段③
D. 段④

答案：
C 如图，连接BE，CE，CF，BE，CF交于点O，则O为正六边形的中心。
∵正六边形的每个中心角都是60°，边长为2，
∴EB = 4。
∵正六边形的每个内角都是120°，
∴∠CDE = 120°，
∴∠DCE = ∠DEC = 30°，
∴∠BCE = 120° - 30° = 90°。在Rt△BCE中，BC = 2，则CE = $\sqrt{BE^{2}-BC^{2}}$ = 2$\sqrt{3}$。
∵∠OFE = ∠AOF = 60°，
∴AD//EF。
∵∠OFE = ∠OCB = 60°，
∴BC//EF，
∴EF//AD//BC。又
∵BE = 2OB，
∴ME = 2MN。
∵CE ＜ ME ＜ BE，即2$\sqrt{3}$ ＜ ME ＜ 4，
∴$\sqrt{3}$ ＜ MN ＜ 2。