第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
如图1,在⊙O中,AC是⊙O的直径,PA与⊙O相切于点A,点B在⊙O上,且PB = PA.

【基础设问】
(1)求证:PB是⊙O的切线.
(2)连接AB,若AC = 10,∠BAC = 30°.
①求∠ABP的度数和△PAB的周长;
②若AB为一个正多边形的一条边,P为正多边形的中心,求该正多边形的面积.
【能力设问】
(3)如图2,AC,PB的延长线相交于点D,若CD = 1,cos∠APD = $\frac{2}{5}$,求⊙O的半径.

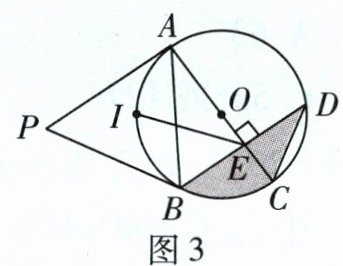
(4)如图3,过点B作BD⊥AC于点E,交⊙O于点D. 若BD = PA = 2$\sqrt{3}$.
①求图中阴影部分的面积(结果保留π);
②若△PAB的内切圆圆心为点I,连接IE,求线段IE的长.

【基础设问】
(1)求证:PB是⊙O的切线.
(2)连接AB,若AC = 10,∠BAC = 30°.
①求∠ABP的度数和△PAB的周长;
②若AB为一个正多边形的一条边,P为正多边形的中心,求该正多边形的面积.
【能力设问】
(3)如图2,AC,PB的延长线相交于点D,若CD = 1,cos∠APD = $\frac{2}{5}$,求⊙O的半径.

(4)如图3,过点B作BD⊥AC于点E,交⊙O于点D. 若BD = PA = 2$\sqrt{3}$.
①求图中阴影部分的面积(结果保留π);
②若△PAB的内切圆圆心为点I,连接IE,求线段IE的长.

答案:
**证明**:连接$PO$,$OB$。 因为$PA$与$\odot O$相切于点$A$,所以$PA\perp CA$,则$\angle PAO = 90^{\circ}$。 又因为$PA = PB$,$OA = OB$,$OP = OP$, 所以$\triangle PAO\cong\triangle PBO(SSS)$,所以$\angle PBO = \angle PAO = 90^{\circ}$,即$PB\perp OB$。 由于$OB$为半径,所以$PB$为$\odot O$的切线。@@①连接$BC$。 因为$AC$是$\odot O$的直径,所以$\angle ABC = 90^{\circ}$。 因为$\angle BAC = 30^{\circ}$,所以$BC=\frac{1}{2}AC = 5$, 所以$AB = \sqrt{AC^{2}-BC^{2}} = 5\sqrt{3}$。 因为$PA$是$\odot O$的切线,所以$\angle OAP = 90^{\circ}$, 所以$\angle PAB = \angle OAP-\angle BAC = 60^{\circ}$。 又因为$PA = PB$,所以$\triangle PAB$是等边三角形, 所以$PA = PB = AB = 5\sqrt{3}$, 所以$\triangle PAB$的周长为$PA + PB + AB = 15\sqrt{3}$。@@②由①知$\angle APB = 60^{\circ}$,所以该正多边形的边数为$\frac{360^{\circ}}{60^{\circ}} = 6$,该正多边形为正六边形。 过点$P$作$PM\perp AB$,由①知$PA = 5\sqrt{3}$, 所以$PM = PA\cdot\cos30^{\circ}=PA\cdot\frac{\sqrt{3}}{2}=\frac{15}{2}$, 所以$S_{\triangle PAB}=\frac{1}{2}\times\frac{15}{2}\times5\sqrt{3}=\frac{75\sqrt{3}}{4}$, 所以该正六边形的面积为$6\times\frac{75\sqrt{3}}{4}=\frac{225\sqrt{3}}{2}$。@@
(3) **解**:连接$OB$。因为$PB$为$\odot O$的切线,所以$\angle OBD = 90^{\circ}$。 因为$\angle PAD = \angle OBD = 90^{\circ}$,$\angle D = \angle D$, 所以$\triangle APD\sim\triangle BOD$,所以$\angle APD = \angle BOD$, 所以$\cos\angle BOD = \cos\angle APD=\frac{2}{5}$。 设$\odot O$的半径为$r$,在$Rt\triangle BOD$中,$OB = OC = r$,$OD = r + 1$, 因为$\cos\angle BOD=\frac{OB}{OD}=\frac{2}{5}$,所以$\frac{r}{r + 1}=\frac{2}{5}$,解得$r=\frac{2}{3}$。 经检验,当$r=\frac{2}{3}$时,$r + 1\neq0$, 所以$r=\frac{2}{3}$是原方程的解,所以$\odot O$的半径是$\frac{2}{3}$。@@①如图,作$BF\perp AP$于点$F$,连接$OB$。 因为$BD\perp AC$,所以$BE = DE=\sqrt{3}$,$\angle AEB = 90^{\circ}$。 又因为$AC\perp PA$, 所以四边形$AEBF$是矩形,所以$AF = BE=\sqrt{3}$。 因为$PA = 2\sqrt{3}$,所以$AF = PF$,所以$AB = PB$。 因为$PB = PA$,所以$\triangle PAB$是等边三角形, 所以$\angle PAB = 60^{\circ}$,所以$\angle BAC = 30^{\circ}$,所以$\angle BOC = 60^{\circ}$。 在$Rt\triangle OBE$中,$OB=\frac{BE}{\sin60^{\circ}} = 2$,$OE = OB\cdot\cos60^{\circ}=1$。 所以$EC = OC - OE = 1 = OE$。 在$\triangle OBE$和$\triangle CDE$中,$BE = DE$,$\angle OEB = \angle CED = 90^{\circ}$,$OE = EC$, 所以$\triangle OBE\cong\triangle CDE(SAS)$,所以$S_{\triangle CDE}=S_{\triangle OBE}$, 所以$S_{阴影}=S_{扇形OBC}=\frac{60\cdot\pi\cdot2^{2}}{360}=\frac{2}{3}\pi$。@@②如图,连接$OP$,$EP$, 因为$\triangle PAB$是等边三角形, 所以$\angle ABF = 30^{\circ}$,所以$BF=\frac{AF}{\tan30^{\circ}} = 3$。 又因为点$I$为$\triangle PAB$的内心,所以点$I$为$BF$,$OP$的交点, 则$\angle API = \angle BPI = \angle PBI = 30^{\circ}$,所以$PI = BI$, 所以$IF=\frac{1}{2}PI=\frac{1}{2}BI$,所以$BI=\frac{2}{3}BF = 2$。 所以在$Rt\triangle BIE$中,$IE=\sqrt{BE^{2}+BI^{2}}=\sqrt{3 + 4}=\sqrt{7}$。
**证明**:连接$PO$,$OB$。 因为$PA$与$\odot O$相切于点$A$,所以$PA\perp CA$,则$\angle PAO = 90^{\circ}$。 又因为$PA = PB$,$OA = OB$,$OP = OP$, 所以$\triangle PAO\cong\triangle PBO(SSS)$,所以$\angle PBO = \angle PAO = 90^{\circ}$,即$PB\perp OB$。 由于$OB$为半径,所以$PB$为$\odot O$的切线。@@①连接$BC$。 因为$AC$是$\odot O$的直径,所以$\angle ABC = 90^{\circ}$。 因为$\angle BAC = 30^{\circ}$,所以$BC=\frac{1}{2}AC = 5$, 所以$AB = \sqrt{AC^{2}-BC^{2}} = 5\sqrt{3}$。 因为$PA$是$\odot O$的切线,所以$\angle OAP = 90^{\circ}$, 所以$\angle PAB = \angle OAP-\angle BAC = 60^{\circ}$。 又因为$PA = PB$,所以$\triangle PAB$是等边三角形, 所以$PA = PB = AB = 5\sqrt{3}$, 所以$\triangle PAB$的周长为$PA + PB + AB = 15\sqrt{3}$。@@②由①知$\angle APB = 60^{\circ}$,所以该正多边形的边数为$\frac{360^{\circ}}{60^{\circ}} = 6$,该正多边形为正六边形。 过点$P$作$PM\perp AB$,由①知$PA = 5\sqrt{3}$, 所以$PM = PA\cdot\cos30^{\circ}=PA\cdot\frac{\sqrt{3}}{2}=\frac{15}{2}$, 所以$S_{\triangle PAB}=\frac{1}{2}\times\frac{15}{2}\times5\sqrt{3}=\frac{75\sqrt{3}}{4}$, 所以该正六边形的面积为$6\times\frac{75\sqrt{3}}{4}=\frac{225\sqrt{3}}{2}$。@@
(3) **解**:连接$OB$。因为$PB$为$\odot O$的切线,所以$\angle OBD = 90^{\circ}$。 因为$\angle PAD = \angle OBD = 90^{\circ}$,$\angle D = \angle D$, 所以$\triangle APD\sim\triangle BOD$,所以$\angle APD = \angle BOD$, 所以$\cos\angle BOD = \cos\angle APD=\frac{2}{5}$。 设$\odot O$的半径为$r$,在$Rt\triangle BOD$中,$OB = OC = r$,$OD = r + 1$, 因为$\cos\angle BOD=\frac{OB}{OD}=\frac{2}{5}$,所以$\frac{r}{r + 1}=\frac{2}{5}$,解得$r=\frac{2}{3}$。 经检验,当$r=\frac{2}{3}$时,$r + 1\neq0$, 所以$r=\frac{2}{3}$是原方程的解,所以$\odot O$的半径是$\frac{2}{3}$。@@①如图,作$BF\perp AP$于点$F$,连接$OB$。 因为$BD\perp AC$,所以$BE = DE=\sqrt{3}$,$\angle AEB = 90^{\circ}$。 又因为$AC\perp PA$, 所以四边形$AEBF$是矩形,所以$AF = BE=\sqrt{3}$。 因为$PA = 2\sqrt{3}$,所以$AF = PF$,所以$AB = PB$。 因为$PB = PA$,所以$\triangle PAB$是等边三角形, 所以$\angle PAB = 60^{\circ}$,所以$\angle BAC = 30^{\circ}$,所以$\angle BOC = 60^{\circ}$。 在$Rt\triangle OBE$中,$OB=\frac{BE}{\sin60^{\circ}} = 2$,$OE = OB\cdot\cos60^{\circ}=1$。 所以$EC = OC - OE = 1 = OE$。 在$\triangle OBE$和$\triangle CDE$中,$BE = DE$,$\angle OEB = \angle CED = 90^{\circ}$,$OE = EC$, 所以$\triangle OBE\cong\triangle CDE(SAS)$,所以$S_{\triangle CDE}=S_{\triangle OBE}$, 所以$S_{阴影}=S_{扇形OBC}=\frac{60\cdot\pi\cdot2^{2}}{360}=\frac{2}{3}\pi$。@@②如图,连接$OP$,$EP$, 因为$\triangle PAB$是等边三角形, 所以$\angle ABF = 30^{\circ}$,所以$BF=\frac{AF}{\tan30^{\circ}} = 3$。 又因为点$I$为$\triangle PAB$的内心,所以点$I$为$BF$,$OP$的交点, 则$\angle API = \angle BPI = \angle PBI = 30^{\circ}$,所以$PI = BI$, 所以$IF=\frac{1}{2}PI=\frac{1}{2}BI$,所以$BI=\frac{2}{3}BF = 2$。 所以在$Rt\triangle BIE$中,$IE=\sqrt{BE^{2}+BI^{2}}=\sqrt{3 + 4}=\sqrt{7}$。

查看更多完整答案,请扫码查看


