《2025年一遍过九年级数学下册冀教版》

9 [2024石家庄二十八中月考]如图,$\odot O$的半径为2,$C_{1}$是函数$y = x^{2}$的图像,$C_{2}$是函数$y = -x^{2}$的图像,则阴影部分的面积是 （ ）

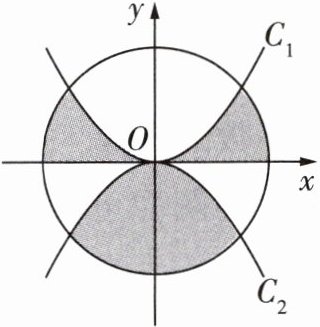
A. $\pi$
B. $2\pi$
C. $4\pi$
D. 都不对

答案： B@@$\because$函数$y = x^{2}$的图像和函数$y = -x^{2}$的图像关于$x$轴对称，（$|a|$相等，抛物线的开口大小相同，$-1$与$1$的绝对值相等，符号相反，故抛物线的开口大小相同，方向相反）$\therefore$题图中阴影部分的面积是圆面积的一半。又$\because$圆的半径为$2$，$\therefore$阴影部分的面积为$\frac{1}{2}\pi\times2^{2}=2\pi$。

10 [2023廊坊广阳区期末]已知点$A( -1,m),B(1,m),C(2,m - 3)$在同一个函数的图像上,则这个函数可能是 （ ）
A. $y = 2x - 3$
B. $y = -\frac{2}{x}$
C. $y = -2x^{2}$
D. $y = -x^{2}$

答案： D@@$\because A(-1,m)$，$B(1,m)$，$\therefore$点$A$与点$B$关于$y$轴对称，故 A，B 项不符合题意；把$B(1,m)$的坐标代入$y = -2x^{2}$，得$m = -2$，$\therefore C(2,-5)$，将$x = 2$代入$y = -2x^{2}$，得$y = -8$，故 C 项不符合题意，同理可知 D 项符合题意。

11 [2024廊坊安次区月考]当$ab ＞ 0$时,$y = ax^{2}$与$y = ax + b$的图像大致是 （ ）

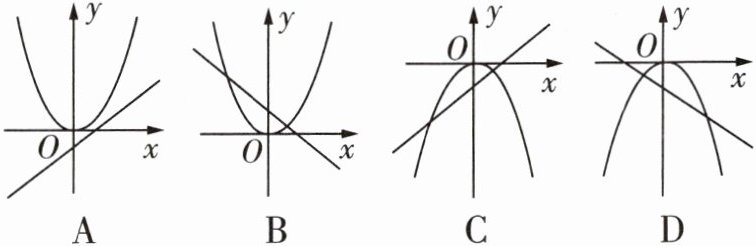
答案： D@@$\because ab＞0$，$\therefore a$，$b$同号，当$a＞0$时，$b＞0$，$y = ax^{2}$的图像开口向上，过原点，$y = ax + b$的图像过第一、二、三象限，此时没有选项符合；当$a＜0$时，$b＜0$，$y = ax^{2}$的图像开口向下，过原点，$y = ax + b$的图像过第二、三、四象限，此时选项 D 中图像符合。

12 [2023秦皇岛一模]如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3). 若抛物线$y = ax^{2}$与正方形有公共点,则实数$a$的取值范围是 （ ）

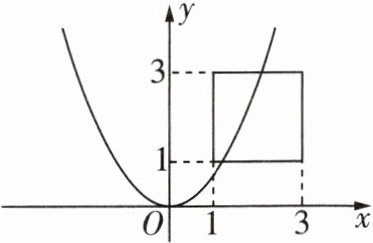
A. $\frac{1}{9}\leqslant a\leqslant 3$
B. $\frac{1}{9}\leqslant a\leqslant 1$
C. $\frac{1}{3}\leqslant a\leqslant 3$
D. $\frac{1}{3}\leqslant a\leqslant 1$

答案： A@@当抛物线经过点$(1,3)$时，$3 = a\cdot1^{2}$，解得$a = 3$。当抛物线经过点$(3,1)$时，$1 = a\cdot3^{2}$，解得$a = \frac{1}{9}$。$\because$抛物线开口向上，$\therefore a$的值越大，开口越小，$\therefore$当抛物线与正方形有公共点时，$\frac{1}{9}\leq a\leq3$。

13 [一题多解][2024邢台英华教育集团检测]如图所示的四个二次函数图像分别对应①$y = ax^{2}$,②$y = bx^{2}$,③$y = cx^{2}$,④$y = dx^{2}$,则$a,b,c,d$的大小关系为_______. (用“＞”连接)

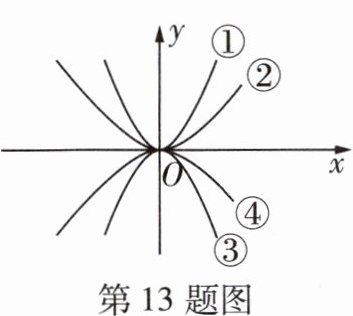
答案： $a＞b＞d＞c$@@解法一 由题中图像，知$a$，$b$均为正数，$c$，$d$均为负数，因为二次项系数的绝对值越大，图像的开口越小，所以$a＞b＞d＞c$。 解法二 因为直线$x = 1$与四条抛物线的交点从上到下依次为$(1,a)$，$(1,b)$，$(1,d)$，$(1,c)$，所以$a＞b＞d＞c$。

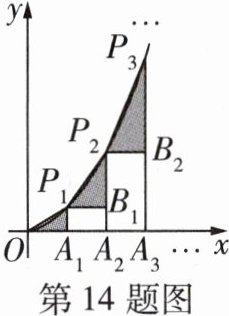
14 如图,已知$A_{1},A_{2},A_{3},\cdots,A_{n}$是$x$轴上的点,且$OA_{1} = A_{1}A_{2} = A_{2}A_{3} = A_{3}A_{4} = \cdots = A_{n - 1}A_{n} = 1$,分别过点$A_{1},A_{2},A_{3},\cdots,A_{n}$作$x$轴的垂线交二次函数$y = \frac{1}{2}x^{2}(x ＞ 0)$的图像于点$P_{1},P_{2},P_{3},\cdots,P_{n}$. 若记$\triangle OA_{1}P_{1}$的面积为$S_{1}$,过点$P_{1}$作$P_{1}B_{1}\perp A_{2}P_{2}$于点$B_{1}$,记$\triangle P_{1}B_{1}P_{2}$的面积为$S_{2}$,过点$P_{2}$作$P_{2}B_{2}\perp A_{3}P_{3}$于点$B_{2}$,记$\triangle P_{2}B_{2}P_{3}$的面积为$S_{3}\cdots\cdots$依次进行下去,则$S_{3} = $_______,记$\triangle P_{n - 1}B_{n - 1}P_{n}(n ＞ 1)$的面积为$S_{n}$,则$S_{n} = $_______.

答案： $\frac{5}{4}$@@$\frac{2n - 1}{4}$@@当$x = 1$时，$y = \frac{1}{2}x^{2}=\frac{1}{2}$，则$P_{1}(1,\frac{1}{2})$，所以$S_{1}=\frac{1}{2}\times1\times\frac{1}{2}=\frac{1}{4}$；当$x = 2$时，$y = \frac{1}{2}x^{2}=2$，则$P_{2}(2,2)$，所以$S_{2}=\frac{1}{2}\times1\times(2 - \frac{1}{2})=\frac{3}{4}$；当$x = 3$时，$y = \frac{1}{2}x^{2}=\frac{9}{2}$，则$P_{3}(3,\frac{9}{2})$，所以$S_{3}=\frac{1}{2}\times1\times(\frac{9}{2}-2)=\frac{5}{4}$，同理可得$S_{n}=\frac{2n - 1}{4}$。

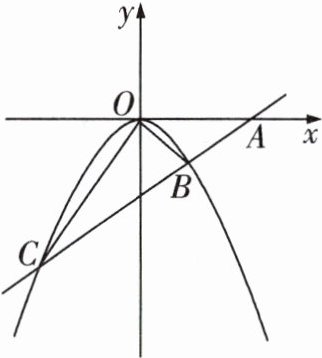
15 如图,已知直线$AB$过$x$轴上一点$A(2,0)$,且与抛物线$y = ax^{2}$相交于$B(1, -1),C$两点.
(1)求抛物线对应的函数表达式.
(2)抛物线上是否存在一点$D$,使$S_{\triangle OAD} = S_{\triangle OBC}$? 若存在,请求出点$D$的坐标;若不存在,请说明理由.

答案： 解：
(1)将$B(1,-1)$的坐标代入$y = ax^{2}$， 得$-1 = a\cdot1^{2}$，解得$a = -1$， $\therefore$抛物线对应的函数表达式为$y = -x^{2}$。
(2)存在。 设直线$AB$的函数表达式为$y = kx + b$， $\because$直线过点$A(2,0)$，$B(1,-1)$， $\therefore\begin{cases}2k + b = 0\\k + b = -1\end{cases}$，解得$\begin{cases}k = 1\\b = -2\end{cases}$， $\therefore$直线$AB$的函数表达式为$y = x - 2$。 由$\begin{cases}y = x - 2\\y = -x^{2}\end{cases}$，解得$\begin{cases}x_{1}=1\\y_{1}=-1\end{cases}$，$\begin{cases}x_{2}=-2\\y_{2}=-4\end{cases}$， $\because B(1,-1)$，$\therefore C(-2,-4)$。 由题图可知，$S_{\triangle OBC}=S_{\triangle OAC}-S_{\triangle OAB}=\frac{1}{2}\times4\times2-\frac{1}{2}\times1\times2 = 3$。 假设抛物线上存在一点$D$，使$S_{\triangle OAD}=S_{\triangle OBC}$。 可设$D(t,-t^{2})$，则$S_{\triangle OAD}=\frac{1}{2}\times2\cdot t^{2}=3$， 解得$t_{1}=\sqrt{3}$，$t_{2}=-\sqrt{3}$， $\therefore$存在符合题意的点$D$，其坐标为$(\sqrt{3},-3)$或$(-\sqrt{3},-3)$。