《2025年一遍过九年级数学下册冀教版》

8 小明与小刚一起玩抛掷两枚硬币的游戏，游戏规则如下：抛出两个正面，小明赢1分；抛出其他结果，小刚赢1分；谁先到10分，谁就获胜. 这是个不公平的游戏，要把它修改成公平的游戏，下列做法错误的是 （ ）
A. 把“抛出两个正面”改为“抛出两个同面”
B. 把“抛出其他结果”改为“抛出两个反面”
C. 把“小明赢1分”改为“小明赢3分”
D. 把“小刚赢1分”改为“小刚赢3分”

答案： D@@抛掷两枚硬币，有4种等可能的结果，分别为（正，正），（正，反），（反，正），（反，反）。A选项，抛出两个同面的概率为$\frac{1}{2}$，抛出其他结果的概率为$\frac{1}{2}$，此时游戏公平；B选项，把“抛出其他结果”改为“抛出两个反面”时，两人获胜的概率都为$\frac{1}{4}$，此时游戏公平；C选项，小明获胜的概率为$\frac{1}{4}$，小刚获胜的概率为$\frac{3}{4}$，故把“小明赢1分”改为“小明赢3分”，此时游戏公平；D选项，把“小刚赢1分”改为“小刚赢3分”，此时游戏不公平。

9 [2023连云港中考] 如图是由16个相同的小正方形和4个相同的大正方形组成的图形，在这个图形内任取一点$P$，则点$P$落在阴影部分的概率为 （ ）
A. $\frac{5}{8}$
B. $\frac{13}{50}$
C. $\frac{13}{32}$
D. $\frac{5}{16}$

答案： B@@解题思路：找出大正方形和小正方形边长的关系，用未知数表示阴影部分的面积和这个图形的面积，求它们的比值并约去未知数即可得到所求概率。 设16个相同的小正方形的边长为a，则4个相同的大正方形的边长为1.5a，故点P落在阴影部分的概率为$\frac{2a^{2}+2\times(1.5a)^{2}}{16a^{2}+4\times(1.5a)^{2}}=\frac{13}{50}$。

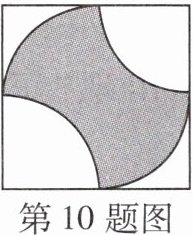
10 一题多解 [2023烟台中考] 如图，在正方形中，阴影部分是分别以正方形的两个顶点及其对称中心为圆心，以正方形边长的一半为半径作弧形成的封闭图形. 将一个小球在该正方形内自由滚动，小球随机地停在正方形内的某一点上. 若小球停在阴影部分的概率为$P_{1}$，停在空白部分的概率为$P_{2}$，则$P_{1}$与$P_{2}$的大小关系为 （ ）

A. $P_{1}＜P_{2}$
B. $P_{1}=P_{2}$
C. $P_{1}＞P_{2}$
D. 无法判断

答案：
B@@通解：如图，连接正方形对边的中点，将正方形分为四个全等的小正方形，设正方形的边长为2a，则空白部分的面积为$2\times\frac{1}{4}\times\pi a^{2}+2(a^{2}-\frac{1}{4}\times\pi a^{2})=\frac{1}{2}\pi a^{2}+2a^{2}-\frac{1}{2}\pi a^{2}=2a^{2}$，则阴影部分的面积为$(2a)^{2}-2a^{2}=4a^{2}-2a^{2}=2a^{2}$，所以小球停在阴影部分的概率等于停在空白部分的概率，即$P_{1}=P_{2}$。 秒解：如图，连接正方形对边的中点，将正方形分为四个全等的小正方形，将左上角小正方形内的阴影部分分割补到右上角的小正方形内的空白处，则上方阴影部分可以构成一个完整的小正方形，同理下方阴影部分也可以构成一个完整的小正方形，所以阴影部分面积占总面积的$\frac{1}{2}$，空白部分面积也占总面积的$\frac{1}{2}$，所以小球停在阴影部分的概率等于停在空白部分的概率，即$P_{1}=P_{2}$。 归纳总结：求不规则图形的面积时，应通过辅助线来将不规则的图形分割成规则的图形，再根据已知或者所设的数据求解。

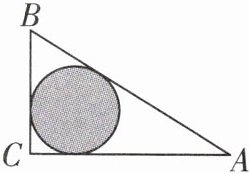
11 [2023石家庄期末] 一块绿化带的形状是如图所示的直角三角形$ABC$，$\angle C = 90^{\circ}$，阴影部分是$\triangle ABC$的内切圆，将阴影部分修建成花圃，已知$AB = 10$，$AC = 8$，一只自由飞翔的小鸟随机飞到这块绿化带上，则小鸟正好落在花圃上的概率为 （ ）

A. $\frac{\pi}{6}$
B. $\frac{\pi}{10}$
C. $\frac{\pi}{12}$
D. $\frac{2\pi}{15}$

答案：
A@@如图，设⊙O的半径为r，在Rt△ABC中，AB = 10，AC = 8，∠C = 90°，由勾股定理得BC = 6，设AC，BC，AB与⊙O的切点分别为点E，D，F，连接OD，OE，则OD⊥BC，OE⊥AC，所以∠ODC = ∠OEC = ∠C = 90°，所以四边形ODCE是矩形。因为⊙O是△ABC的内切圆，所以CD = CE，BD = BF，AF = AE，所以四边形ODCE是正方形，所以CD = OD = r，BD = BF = 6 - r，AF = AE = 8 - r，所以6 - r + 8 - r = 10，解得r = 2，所以圆的面积为$2^{2}\times\pi=4\pi$。因为$S_{\triangle ABC}=\frac{1}{2}AC\times BC=\frac{1}{2}\times8\times6 = 24$，所以小鸟正好落在花圃上的概率为$\frac{4\pi}{24}=\frac{\pi}{6}$。

12 [2024西安长安区期末] 一个不透明的口袋中有20个球（每个球除颜色外其他均相同），其中白球有$x$个，绿球有$2x$个，其余为黑球. 从袋中任意摸出一个球，若为绿球，则甲胜；若为黑球，则乙胜；若为白球，则需重摸. 当$x =$_______时，游戏对甲、乙双方公平.

答案： 4 设A = “摸到绿球”，B = “摸到黑球”，由题意知，黑球的个数为20 - 3x，则$P(A)=\frac{2x}{20}$，$P(B)=\frac{20 - 3x}{20}$，要使游戏对甲、乙双方公平，则$P(A)=P(B)$，即$\frac{2x}{20}=\frac{20 - 3x}{20}$，解得x = 4。

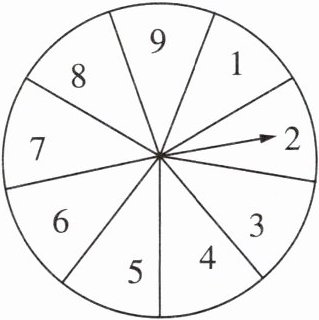
13 运算能力 教材P65练习T2变式 [2024武威模拟] 小亮和小芳都想参加学校社团组织的暑假实践活动，但只有一个名额，小亮提议通过玩转盘的游戏决定谁去参加活动，规则如下：将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，若转到4的倍数，小亮去参加活动；若转到3的倍数，小芳去参加活动；若转到其他号码，则重新转动转盘.
(1) 转盘转到4的倍数的概率是多少？
(2) 你认为这个游戏公平吗？若公平，请说明理由；若不公平，请修改规则，使游戏公平.

答案： 解：（1）转动转盘共有1，2，3，4，5，6，7，8，9这9种可能结果，每种结果的可能性相等，其中转到4的倍数的结果有2种，分别是4，8，
∴$P(转到4的倍数)=\frac{2}{9}$。 （2）这个游戏不公平。理由如下： 由（1）知，$P(转到4的倍数)=\frac{2}{9}$，
∴小亮去参加活动的概率为$\frac{2}{9}$。
∵转到3的倍数的结果有3种，分别是3，6，9，
∴$P(转到3的倍数)=\frac{3}{9}=\frac{1}{3}$，
∴小芳去参加活动的概率为$\frac{1}{3}$。
∵$\frac{2}{9}\neq\frac{1}{3}$，
∴这个游戏不公平。 若使游戏公平，则可将规则改为“将一个转盘9等分，分别标上1至9九个号码，随意转动转盘，若转到的数小于5，小亮去参加活动；若转到的数大于5，小芳去参加活动；若转到5，则重新转动转盘（答案不唯一）”。