第51页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
1 如图,二次函数$y = x^{2}+bx + c$的图像与$x$轴交于点$A,B(3,0)$,与$y$轴交于点$C(0, - 3)$,顶点为$M$.
【基础设问】
(1)求该二次函数的表达式,并写出该函数图像的对称轴和顶点坐标.
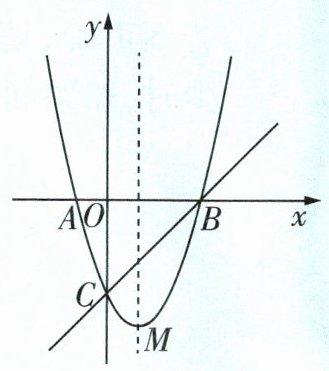
(2)当$x$______时,$y$随$x$的增大而增大.
(3)不等式$x^{2}+bx + c>0$的解集是______.
(4)当$0\leqslant x\leqslant4$时,函数值$y$的取值范围是______.
【能力设问】
(5)若点$E$是对称轴上的一动点,当$\triangle EAC$的周长最小时,求点$E$的坐标.
(6)将直线$BC$向下平移$m$个单位长度,平移后的直线与抛物线有且仅有一个公共点,求$m$的值.
(7)在第四象限的抛物线上有一点$F$,连接$BF,CF$,求四边形$ABFC$的面积的最大值及此时点$F$的坐标.
(8)连接$AC$,若点$P$为直线$BC$下方抛物线上一动点,过点$P$作$AC$的平行线$l$,交线段$BC$于点$N$. 在直线$l$上是否存在点$Q$,使得以点$A,C,N,Q$为顶点的四边形为菱形?若存在,求出点$Q$的坐标;若不存在,请说明理由.
【基础设问】
(1)求该二次函数的表达式,并写出该函数图像的对称轴和顶点坐标.

(2)当$x$______时,$y$随$x$的增大而增大.
(3)不等式$x^{2}+bx + c>0$的解集是______.
(4)当$0\leqslant x\leqslant4$时,函数值$y$的取值范围是______.
【能力设问】
(5)若点$E$是对称轴上的一动点,当$\triangle EAC$的周长最小时,求点$E$的坐标.
(6)将直线$BC$向下平移$m$个单位长度,平移后的直线与抛物线有且仅有一个公共点,求$m$的值.
(7)在第四象限的抛物线上有一点$F$,连接$BF,CF$,求四边形$ABFC$的面积的最大值及此时点$F$的坐标.
(8)连接$AC$,若点$P$为直线$BC$下方抛物线上一动点,过点$P$作$AC$的平行线$l$,交线段$BC$于点$N$. 在直线$l$上是否存在点$Q$,使得以点$A,C,N,Q$为顶点的四边形为菱形?若存在,求出点$Q$的坐标;若不存在,请说明理由.
答案:
$>1$@@$x < -1$或$x>3$@@$-4\leq y\leq5$
$>1$@@$x < -1$或$x>3$@@$-4\leq y\leq5$

查看更多完整答案,请扫码查看


