第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
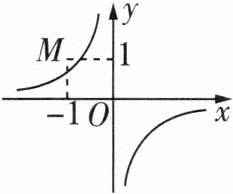
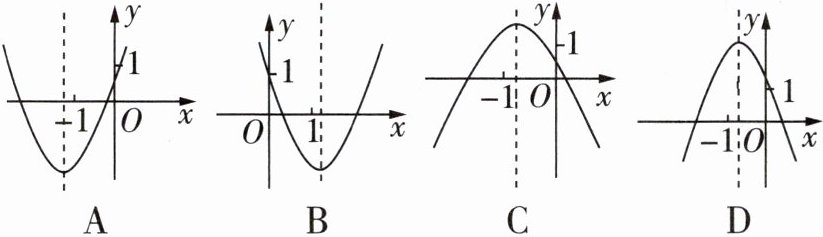
9 [2023秦皇岛海港区期末]已知点$M( -1,1)$与反比例函数$y = \frac{k}{x}$的图像如图所示,则二次函数$y = 2kx^{2}-x + k^{2}$的图像大致为 ( )


答案:
C
10 [2023石家庄外国语教育集团期末]二次函数$y = ax^{2}+bx + c(a,b,c$为常数,且$a\neq0)$中的$x$与$y$的部分对应值如下表. 下列结论错误的是 ( )
| $x$ | $\cdots$ | -1 | 0 | 1 | 2 | 3 | $\cdots$ |
| $y$ | $\cdots$ | 0 | 3 | 4 | 3 | | $\cdots$ |
A. $a < 0$
B. $2a + b = 0$
C. 当$x > 1$时,$y$随$x$的增大而增大
D. 表中盖住的数是0
| $x$ | $\cdots$ | -1 | 0 | 1 | 2 | 3 | $\cdots$ |
| $y$ | $\cdots$ | 0 | 3 | 4 | 3 | | $\cdots$ |
A. $a < 0$
B. $2a + b = 0$
C. 当$x > 1$时,$y$随$x$的增大而增大
D. 表中盖住的数是0
答案:
C
11 [2024上海中考]若二次函数$y = a(x - m)^{2}+k(a\neq0)$中存在一点$P(x',y')$,使得$x' - m = y' - k\neq0$,则称$2|x' - m|$为该抛物线的“开口大小”,那么抛物线$y = -\frac{1}{2}x^{2}+\frac{1}{3}x + 3$的“开口大小”为_______.
答案:
4
12 [新趋势·结论开放]已知函数$y = kx^{2}+(2k + 1)x + 1(k$为实数).
(1)对于任意实数$k$,函数图像一定经过点( -2, -1)和点_______;
(2)对于任意正实数$k$,当$x > m$时,$y$随$x$的增大而增大,写出一个满足题意的$m$的值:_______.
(1)对于任意实数$k$,函数图像一定经过点( -2, -1)和点_______;
(2)对于任意正实数$k$,当$x > m$时,$y$随$x$的增大而增大,写出一个满足题意的$m$的值:_______.
答案:
(1)(0,1)@@
(2)0
(1)(0,1)@@
(2)0
13 [2024邢台新都区三模]点$A(a,b_{1}),B(a + 2,b_{2})$在函数$y = -x^{2}+2x + 3$的图像上,当$a\leqslant x\leqslant a + 2$时,函数的最大值为4,最小值为$b_{1}$,则$a$的取值范围是_______.
答案:
-1⩽a⩽0
-1⩽a⩽0

14 [2024成都中考]在平面直角坐标系$xOy$中,$A(x_{1},y_{1}),B(x_{2},y_{2}),C(x_{3},y_{3})$是二次函数$y = -x^{2}+4x - 1$图像上三点. 若$0 < x_{1} < 1,x_{2} > 4$,则$y_{1}$_______$y_{2}$(填“>”或“<”);若对于$m < x_{1} < m + 1,m + 1 < x_{2} < m + 2,m + 2 < x_{3} < m + 3$,存在$y_{1} < y_{3} < y_{2}$,则$m$的取值范围是_______.
答案:
>@@
>@@

15 [推理能力][2024安徽中考]已知抛物线$y = -x^{2}+bx(b$为常数)的顶点横坐标比抛物线$y = -x^{2}+2x$的顶点横坐标大1.
(1)求$b$的值.
(2)点$A(x_{1},y_{1})$在抛物线$y = -x^{2}+2x$上,点$B(x_{1} + t,y_{1} + h)$在抛物线$y = -x^{2}+bx$上.
(i)若$h = 3t$,且$x_{1}\geqslant0,t > 0$,求$h$的值.
(ii)若$x_{1} = t - 1$,求$h$的最大值.
(1)求$b$的值.
(2)点$A(x_{1},y_{1})$在抛物线$y = -x^{2}+2x$上,点$B(x_{1} + t,y_{1} + h)$在抛物线$y = -x^{2}+bx$上.
(i)若$h = 3t$,且$x_{1}\geqslant0,t > 0$,求$h$的值.
(ii)若$x_{1} = t - 1$,求$h$的最大值.
答案:
15 解:
(1)- 抛物线y = - +bx的顶点横坐标为
(1)- 抛物线y = - +bx的顶点横坐标为
6
-+2x的顶点横坐标为1...·
6
2
-1=1,.6=4.
@@
(2)○ 点A(xj,x)在抛物线y= -x+2x上,
(2)○ 点A(xj,x)在抛物线y= -x+2x上,
二y=-*+2xj-
B(x; +1,y; +h)在抛物线y= -²+4x上,
=y+h=-(x;+0)²+4(x;+0),
. -x²+2x,+h=-(x,+/)²+4(x,+0),
. h=-²-2xj1+2x;+4k.
()“ h=3r,.3t= -²-2xjt+2x;+4t,
.(&+2xj)=t+2xj-
"x;>0,/>0,.1+2x;>0,.1 =1...h =3.
(i)将x,=²-1代人h=-²-2x,t+2x,+4k,
得h=-3²+8r-2=-3(n-告)
²+号
3
=-3<0,
. 当- =-
-,即x, =
时,h取最大值
查看更多完整答案,请扫码查看


