《2025年一遍过九年级数学下册冀教版》

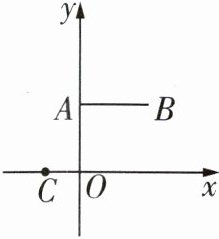
1 [2023湘潭凤凰中学期末]如图，已知$A(0,2)$,$B(2,2)$,$C(-1,0)$，抛物线$y = a(x - h)^2 + k$过点$C$，顶点$M$位于第一象限且在线段$AB$的垂直平分线上，若抛物线与线段$AB$无公共点，则$k$的取值范围是 （ ）

A. $0 ＜ k ＜ 2$
B. $0 ＜ k ＜ 2$或$k ＞ \frac{8}{3}$
C. $k ＞ \sqrt{7}$
D. $0 ＜ k ＜ 2$或$k ＞ \sqrt{7}$

答案： B

2 [新考法][2024福建中考]已知二次函数$y = x^2 - 2ax + a(a \neq 0)$的图像经过$A(\frac{a}{2},y_1)$，$B(3a,y_2)$两点，则下列判断正确的是 （ ）
A. 可以找到一个实数$a$，使得$y_1 ＞ a$
B. 无论实数$a$取什么值，都有$y_1 ＞ a$
C. 可以找到一个实数$a$，使得$y_2 ＜ 0$
D. 无论实数$a$取什么值，都有$y_2 ＜ 0$

答案： C

3 [2023福建中考]已知抛物线$y = ax^2 - 2ax + b(a ＞ 0)$经过$A(2n + 3,y_1)$,$B(n - 1,y_2)$两点，若$A$,$B$分别位于抛物线对称轴的两侧，且$y_1 ＜ y_2$，则$n$的取值范围是__________.

答案： $-1 ＜ n ＜ 0$

4 [新趋势·五育并举][2023黄冈中考]加强劳动教育，落实五育并举. 孝礼中学在当地政府的支持下，建成了一处劳动实践基地. 2023年计划将其中$1\ 000\ m^2$的土地全部种植甲、乙两种蔬菜. 经调查发现：甲种蔬菜种植成本$y$（单位：元/$m^2$）与其种植面积$x$（单位：$m^2$）的函数关系如图所示，其中$200 \leq x \leq 700$，乙种蔬菜的种植成本为$50$元/$m^2$.
(1)当$x = \_\_ m^2$时，$y = 35$元/$m^2$.
(2)设2023年甲、乙两种蔬菜总种植成本为$W$元，如何分配两种蔬菜的种植面积，使$W$最小？
(3)学校计划今后每年在这$1\ 000\ m^2$土地上均按(2)中方案种植蔬菜，因技术改进，预计种植成本逐年下降. 若甲种蔬菜种植成本平均每年下降$10\%$，乙种蔬菜种植成本平均每年下降$a\%$，当$a$为何值时，2025年的总种植成本为$28\ 920$元？

答案： 500

5 [2023衡阳中考]已知$m ＞ n ＞ 0$，若关于$x$的方程$x^2 + 2x - 3 - m = 0$的解为$x_1$,$x_2(x_1 ＜ x_2)$，关于$x$的方程$x^2 + 2x - 3 - n = 0$的解为$x_3$,$x_4(x_3 ＜ x_4)$，则下列结论正确的是 （ ）
A. $x_3 ＜ x_1 ＜ x_2 ＜ x_4$
B. $x_1 ＜ x_3 ＜ x_4 ＜ x_2$
C. $x_1 ＜ x_2 ＜ x_3 ＜ x_4$
D. $x_3 ＜ x_4 ＜ x_1 ＜ x_2$

答案：
B