《2025年一遍过九年级数学下册冀教版》

1 [新考法][2023河北中考]已知二次函数$y=-x^{2}+m^{2}x$和$y = x^{2}-m^{2}$($m$是常数)的图像与$x$轴都有两个交点，且这四个交点中每相邻两点间的距离都相等，则这两个函数图像对称轴之间的距离为 ( )
A. 2
B. $m^{2}$
C. 4
D. $2m^{2}$

答案：
A

2 [一题多解][2020河北中考]如图，现要在抛物线$y = x(4 - x)$上找点$P(a,b)$，针对$b$的不同取值，所找点$P$的个数，三人的说法如下：甲，若$b = 5$，则点$P$的个数为$0$；乙，若$b = 4$，则点$P$的个数为$1$；丙，若$b = 3$，则点$P$的个数为$1$. 下列判断正确的是 ( )

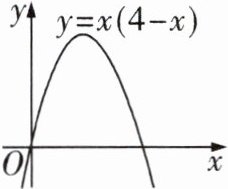
A. 乙错，丙对
B. 甲和乙都错
C. 乙对，丙错
D. 甲错，丙对

答案： C

3 [2024邯郸十三中模拟]已知，二次函数$y = ax^{2}+bx - 1$($a,b$是常数，且$a\neq0$)的图像经过$A(2,1),B(4,3),C(4, - 1)$三个点中的两个点，平移该函数的图像，使其顶点始终在直线$y = x - 1$上，则平移后所得抛物线与$y$轴交点的纵坐标 ( )
A. 有最大值，为$1$
B. 有最大值，为$-\frac{1}{2}$
C. 有最小值，为$1$
D. 有最小值，为$-\frac{1}{2}$

答案： B

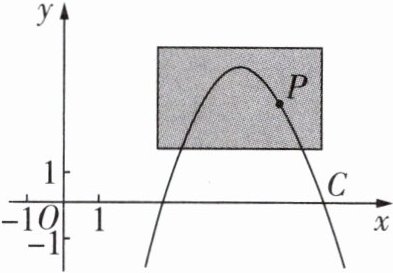
4 [2022河北中考]如图，点$P(a,3)$在抛物线$C$：$y = 4-(6 - x)^{2}$上，且在$C$的对称轴右侧.
(1)写出$C$的对称轴与$y$的最大值，并求$a$的值；
(2)坐标平面上放置一透明胶片，并在胶片上描画出点$P$及$C$的一段，分别记为$P',C'$，平移该胶片，使$C'$所在抛物线对应的函数恰为$y=-x^{2}+6x - 9$，求点$P'$移动的最短路程.

答案：  4. 解： - （1）因为抛物线$C:y = 4-(6 - x)^{2}=-(x - 6)^{2}+4$，所以抛物线的顶点坐标为$Q(6,4)$，对称轴为直线$x = 6$，$y$的最大值为$4$。当$y = 3$时，$3 = -(x - 6)^{2}+4$，所以$x = 5$或$x = 7$。因为点$P$在对称轴的右侧，所以$P(7,3)$，所以$a = 7$。 - @@（2）因为平移后的抛物线的表达式为$y = -(x - 3)^{2}$，所以平移后的抛物线的顶点坐标为$Q'(3,0)$。因为平移前抛物线的顶点坐标为$Q(6,4)$，所以点$P'$移动的最短路程$QQ'=\sqrt{3^{2}+4^{2}}=5$。 

5 [2023河北中考]嘉嘉和淇淇在玩沙包游戏. 某同学借此情境编制了一道数学题，请解答这道题.
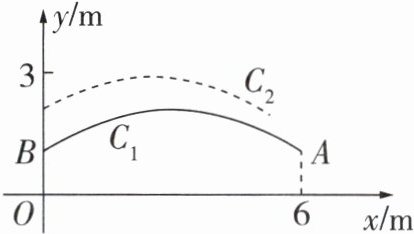
如图，在平面直角坐标系中，一个单位长度代表$1\ m$长. 嘉嘉在点$A(6,1)$处将沙包(看成点)抛出，其运动路线为抛物线$C_{1}:y = a(x - 3)^{2}+2$的一部分，淇淇恰在点$B(0,c)$处接住，然后跳起将沙包回传，其运动路线为抛物线$C_{2}:y=-\frac{1}{8}x^{2}+\frac{n}{8}x + c + 1$的一部分.
(1)写出$C_{1}$的最高点坐标，并求$a,c$的值；
(2)若嘉嘉在$x$轴上方$1\ m$的高度上，且到点$A$水平距离不超过$1\ m$的范围内可以接到沙包，求符合条件的$n$的整数.

答案：
5. 解： - （1）因为抛物线$C_{1}:y = a(x - 3)^{2}+2$，所以抛物线$C_{1}$的顶点坐标为$(3,2)$。因为点$A(6,1)$在抛物线$C_{1}:y = a(x - 3)^{2}+2$上，所以$1 = a(6 - 3)^{2}+2$，所以$a = -\frac{1}{9}$，所以抛物线$C_{1}:y = -\frac{1}{9}(x - 3)^{2}+2$，当$x = 0$时，$y = -\frac{1}{9}(0 - 3)^{2}+2 = 1$，所以$c = 1$。 - @@（2）当抛物线$C_{2}:y = -\frac{1}{8}x^{2}+\frac{n}{8}x + c + 1$经过$(5,1)$时，$1 = -\frac{1}{8}\times25+\frac{n}{8}\times5 + 1 + 1$，解得$n=\frac{17}{5}$。当抛物线$C_{2}:y = -\frac{1}{8}x^{2}+\frac{n}{8}x + c + 1$经过$(7,1)$时，$1 = -\frac{1}{8}\times49+\frac{n}{8}\times7 + 1 + 1$，解得$n=\frac{41}{7}$。因为嘉嘉在$x$轴上方$1m$的高度上，且到点$A$水平距离不超过$1m$的范围内可以接到沙包，所以$\frac{17}{5}\leq n\leq\frac{41}{7}$，所以符合条件的$n$的整数值为$4$和$5$。