《2025年一遍过九年级数学下册冀教版》

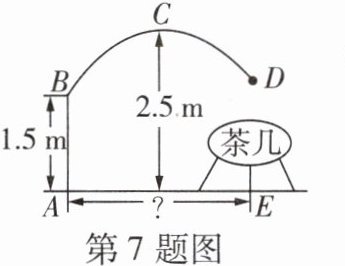
7 [一题多解][2024张家口一模]如图是一款抛物线形落地灯筒示意图，防滑螺母C为抛物线支架的最高点，灯罩D距离地面1.5 m，最高点C距灯柱的水平距离为1.6 m，灯柱AB = 1.5 m，若茶几摆放在灯罩的正下方，则茶几到灯柱的距离AE为 （ ）

A. 3.2 m
B. 0.32 m
C. 2.5 m
D. 1.6 m

答案：
A@@如图，以$AE$所在直线为$x$轴、$AB$所在直线为$y$轴建立平面直角坐标系。 - **优解**：$\because AB = DE = 1.5\ m$，$\therefore$点$B$与点$D$关于对称轴对称，$\therefore AE = 2\times1.6 = 3.2(m)$。 - **通解**：由题意知，抛物线的顶点$C$的坐标为$(1.6,2.5)$，设抛物线的表达式为$y = a(x - 1.6)^{2}+2.5$，将点$B(0,1.5)$代入得，$2.56a + 2.5 = 1.5$，解得$a = -\frac{1}{2.56}$，$\therefore$抛物线的表达式为$y = -\frac{1}{2.56}(x - 1.6)^{2}+2.5$。当$y = 1.5$时，$-\frac{1}{2.56}(x - 1.6)^{2}+2.5 = 1.5$，解得$x = 0$（舍去）或$x = 3.2$，$\therefore$茶几到灯柱的距离$AE$为$3.2\ m$。 

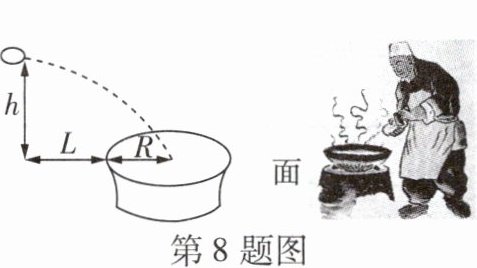
8 [跨学科·物理][2024常德一模]刀削面堪称天下一绝，传统的操作方法是一手托面，一手拿刀，直接将面削到开水锅里. 如图，面刚被削离时与开水锅的高度差h = 0.45 m，与锅的水平距离L = 0.3 m，锅的半径R = 0.5 m. 若将削出的小面圈的运动轨迹视为抛物线的一部分，要使其落入锅中(锅的厚度忽略不计)，则其水平初速度v₀不可能为（提示：h = $\frac{1}{2}$gt²，g = 10 m/s²，水平移动距离s = v₀t） （ ）

A. 2.5 m/s
B. 3 m/s
C. 3.5 m/s
D. 5 m/s

答案： D@@由题意得$\frac{1}{2}\times10t^{2}=0.45$，解得$t_{1}=0.3$，$t_{2}=-0.3$（舍去），$\because$要使其落入锅中，$\therefore L＜s＜L + 2R$，$\therefore0.3＜s＜1.3$，$\therefore0.3＜v_{0}\cdot0.3＜1.3$，$\therefore1＜v_{0}＜\frac{13}{3}$，$\because5＞\frac{13}{3}$，$\therefore5\ m/s$不可能。

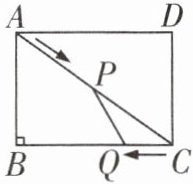
9 如图，在矩形ABCD中，AB = 6 m，BC = 8 m，动点P以2 m/s的速度从点A出发，沿AC向点C移动，同时动点Q以1 m/s的速度从点C出发，沿CB向点B移动，设P，Q两点移动t s(0 ＜ t ＜ 5)后，四边形ABQP的面积为S m².
(1)求面积S与时间t之间的函数关系式.
(2)在P，Q两点移动的过程中，四边形ABQP与△CPQ的面积能否相等？若能，求出此时点P的位置；若不能，请说明理由.

答案：
解： - （1）如图，过点$P$作$PE\perp BC$于点$E$。 在$Rt\triangle ABC$中，$AC=\sqrt{AB^{2}+BC^{2}}=\sqrt{6^{2}+8^{2}} = 10$。 由题意知$AP = 2t$，$CQ = t$，则$PC = 10 - 2t$。 由$AB\perp BC$，$PE\perp BC$得$PE// AB$， $\therefore\frac{PE}{AB}=\frac{PC}{AC}$，即$\frac{PE}{6}=\frac{10 - 2t}{10}$， $\therefore PE=\frac{3}{5}(10 - 2t)=-\frac{6}{5}t + 6$， 又$\because S_{\triangle ABC}=\frac{1}{2}\times6\times8 = 24$， $\therefore S = S_{\triangle ABC}-S_{\triangle PCQ}=24-\frac{1}{2}t(-\frac{6}{5}t + 6)=\frac{3}{5}t^{2}-3t + 24$，即$S=\frac{3}{5}t^{2}-3t + 24$。 - （2）不能。理由如下： 假设四边形$ABQP$与$\triangle CPQ$的面积相等，即$S=\frac{1}{2}S_{\triangle ABC}$，则$\frac{3}{5}t^{2}-3t + 24 = 12$，即$t^{2}-5t + 20 = 0$。 $\because b^{2}-4ac=(-5)^{2}-4\times1\times20＜0$，$\therefore$方程无实数根， $\therefore$在$P$，$Q$两点移动的过程中，四边形$ABQP$与$\triangle CPQ$的面积不能相等。

10 [新情境][2024武汉中考]16世纪中叶，我国发明了一种新式火箭“火龙出水”，它是二级火箭的始祖. 火箭第一级运行路径形如抛物线，当火箭运行一定水平距离时，自动引发火箭第二级，火箭第二级沿直线运行. 某科技小组运用信息技术模拟火箭运行过程. 如图，以发射点为原点，地平线为x轴，垂直于地面的直线为y轴，建立平面直角坐标系，分别得到抛物线y = ax² + x和直线y = -$\frac{1}{2}$x + b. 其中，当火箭运行的距离距离为9 km时，自动引发火箭的第二级.
(1)若火箭第二级的引发点的高度为3.6 km，
①写出写出a，b的值.
②火箭在运行过程中，有两个位置的高度比火箭运行的最高点低1.35 km，求这两个位置之间的距离.
(2)直接写出a满足什么条件时，火箭落地点与发射点的距离超过超过15 km.

答案： 解： - （1）①$a = -\frac{1}{15}$，$b = 8.1$。 $\because y = ax^{2}+x$经过点$(9,3.6)$，$\therefore81a + 9 = 3.6$，解得$a = -\frac{1}{15}$。 $\because y = -\frac{1}{2}x + b$经过点$(9,3.6)$，$\therefore3.6 = -\frac{1}{2}\times9 + b$，解得$b = 8.1$。 ②由①，得$y = -\frac{1}{15}x^{2}+x = -\frac{1}{15}(x^{2}-15x+\frac{225}{4})+\frac{15}{4}=-\frac{1}{15}(x - \frac{15}{2})^{2}+\frac{15}{4}(0\leqslant x\leqslant9)$， $\therefore$火箭运行的最高点是$\frac{15}{4}\ km$，$\therefore\frac{15}{4}-1.35 = 2.4(km)$， $\therefore2.4 = -\frac{1}{15}x^{2}+x$，整理，得$x^{2}-15x + 36 = 0$，解得$x_{1}=12$（舍去），$x_{2}=3$。 由①，得$y = -\frac{1}{2}x + 8.1$， $\therefore2.4 = -\frac{1}{2}x + 8.1$，解得$x = 11.4$， $\therefore11.4 - 3 = 8.4(km)$。 $\therefore$这两个位置之间的距离为$8.4\ km$。 - （2）当$x = 9$时，$y = 81a + 9$， $\therefore$火箭第二级的引发点的坐标为$(9,81a + 9)$。 设火箭落地点与发射点的水平距离为$15\ km$， $\therefore y = -\frac{1}{2}x + b$经过点$(9,81a + 9)$，$(15,0)$， $\therefore\begin{cases}-\frac{1}{2}\times9 + b = 81a + 9\\-\frac{1}{2}\times15 + b = 0\end{cases}$，解得$\begin{cases}a = -\frac{2}{27}\\b=\frac{15}{2}\end{cases}$， $\therefore$当$-\frac{2}{27}＜a＜0$时，火箭落地点与发射点的水平距离超过$15\ km$。